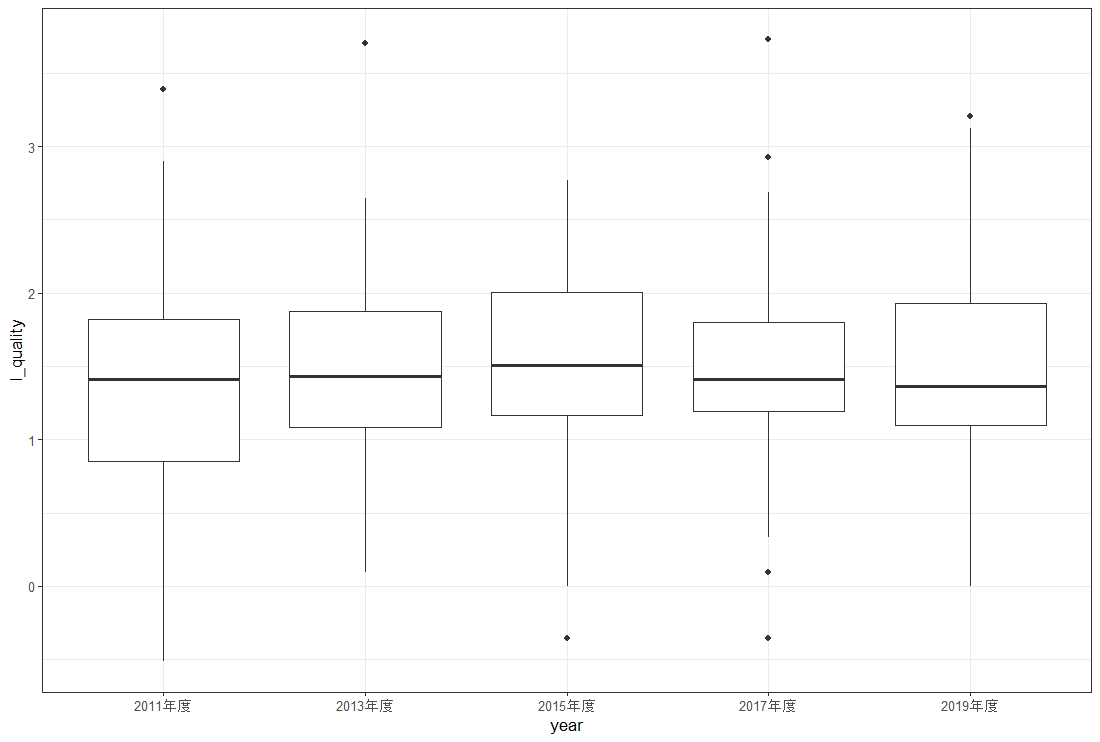Bing Image Creator で生成: North Area Landscape, breezing wind, photograph style
www.crosshyou.info
の続きです。前回は、R の infer パッケージを利用して、ANOVA(Analysis of Variance) 分析をしました。今回は、infer パッケージで Multiple Regression Analysis を実行します。
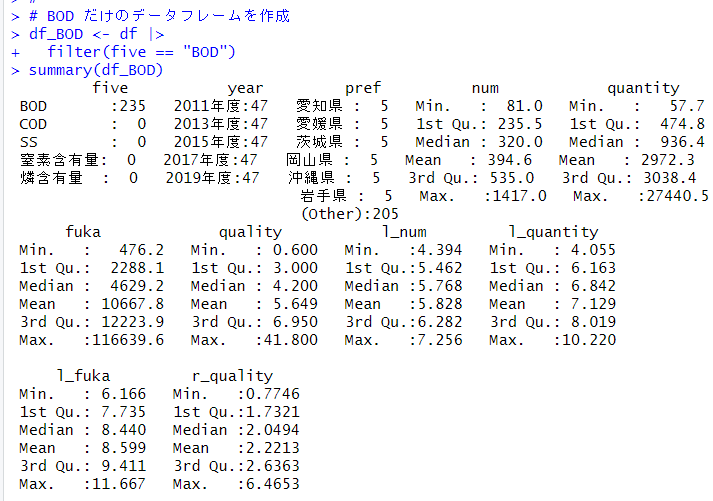
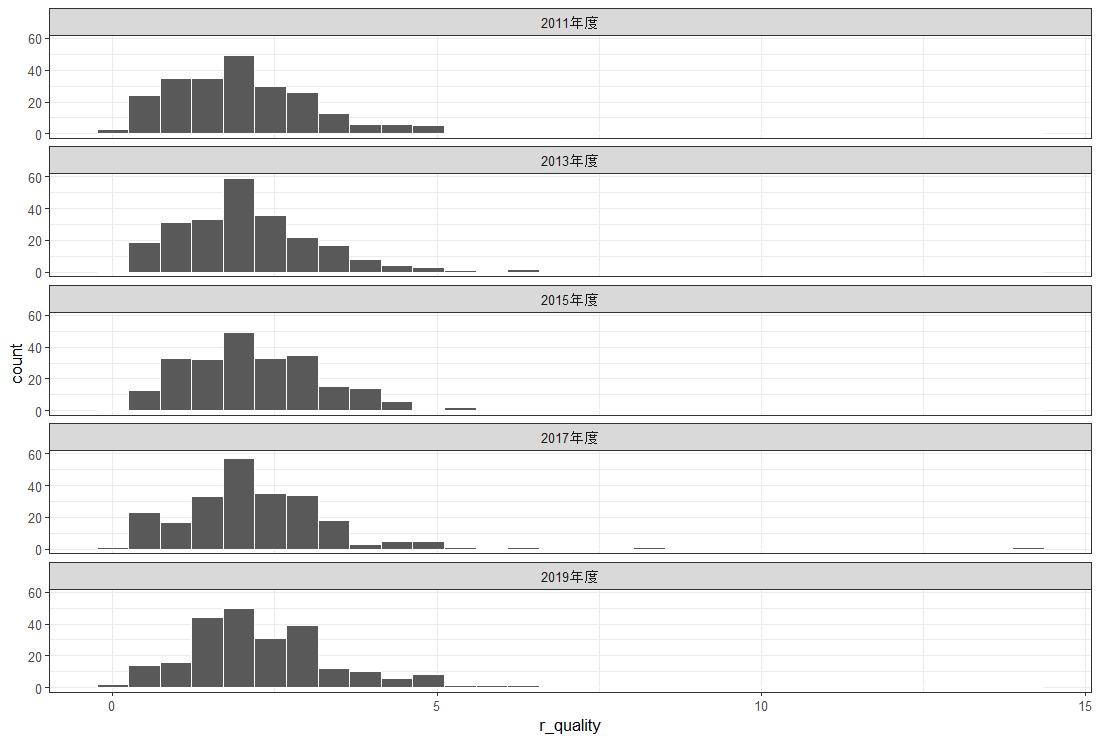
l_quality: 平均水質【mg/l】の対数変換値を被説明変数にして、その他の変数を説明変数にして重回帰分析をしようと思います。
最初に、どの都道府県が l_quality の値が大きいか / 小さいかをグラフにしてみます。


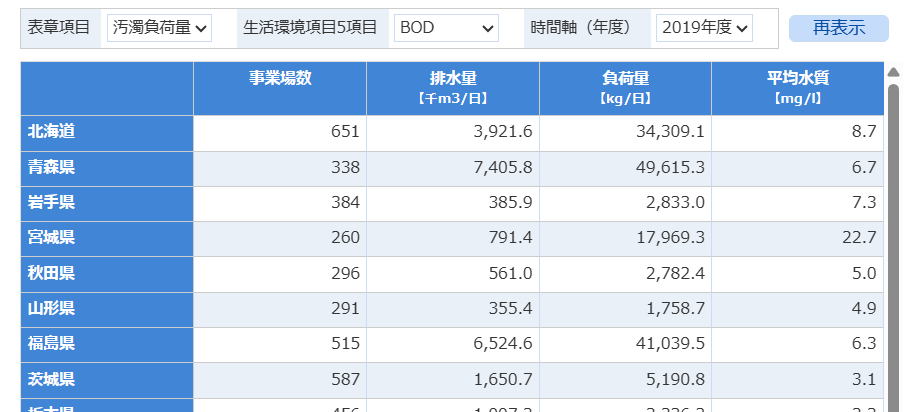
宮城県が一番水質が悪く、神奈川県が一番水質が良い、ということがわかります。東北の件は比較的、水質が悪い感じです。
変数間の相関係数マトリックスを作成します。

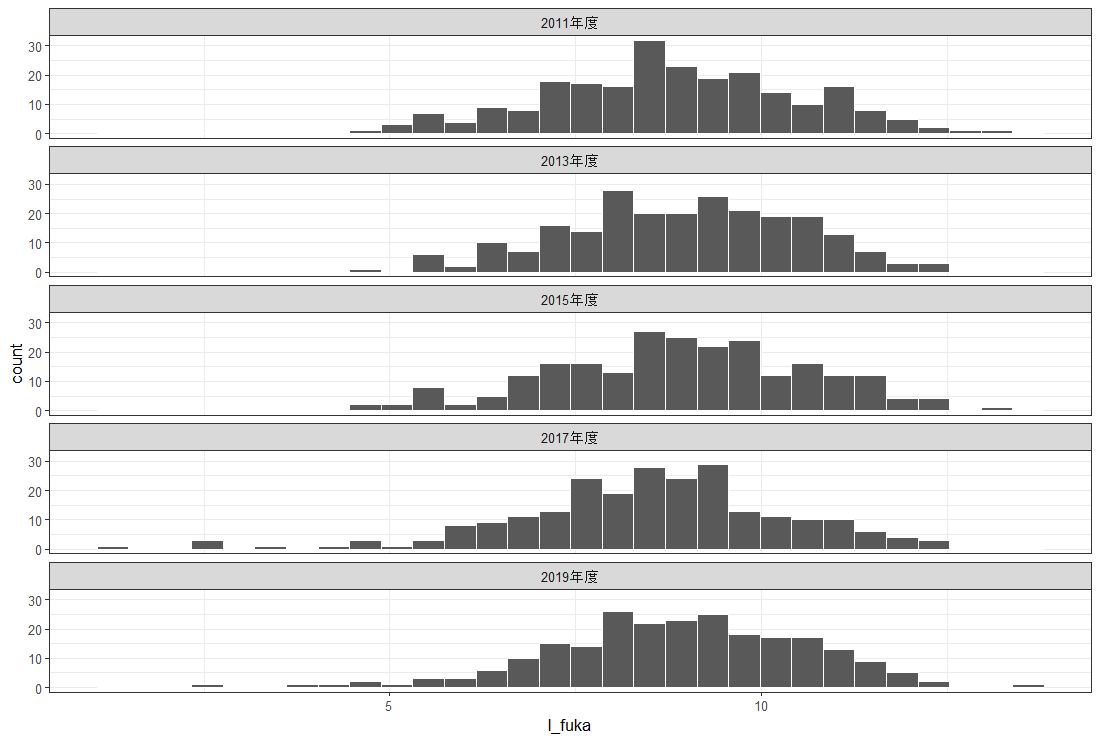
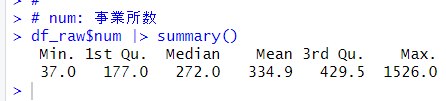
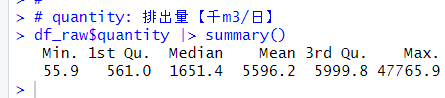
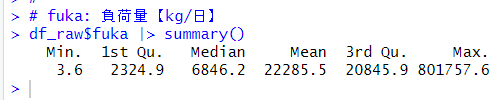
l_quality を説明する変数として、l_num, l_quantity, l_fuka を使おうと思います。
l_quality との相関を考えると、l_num は負の相関、l_quantity は正の相関、l_fuka は正の相関です。
ggcorrplot パッケージを使って、もう少しわかりやすい相関係数マトリックスを作成します。


赤色が濃いと正の相関、青色が濃いと負の相関、とわかりやすいです。
GGally パッケージの ggpairs() 関数で散布図マトリックスを作成します。


ggpairs() 関数は散布図の他に、相関係数も計算してくれて、さらに分布密度も表示してくれます。
それでは、本題、l_quality を l_num, l_quantity, l_fuka で重回帰分析してみましょう。
今回も
Full infer Pipeline Examples • infer
こちらの infer のウェブサイトを参考にしました。
モデルの実際の推定係数をまずだします。

l_quality = 0.00610 - 0.000832 * l_num - 0.997 * l_quantity + 0.998 * l_fuka + u
というモデル式が推定されました。
これらの係数が有意に 0 と違うかどうかが問題です。
null distribution を作成します。

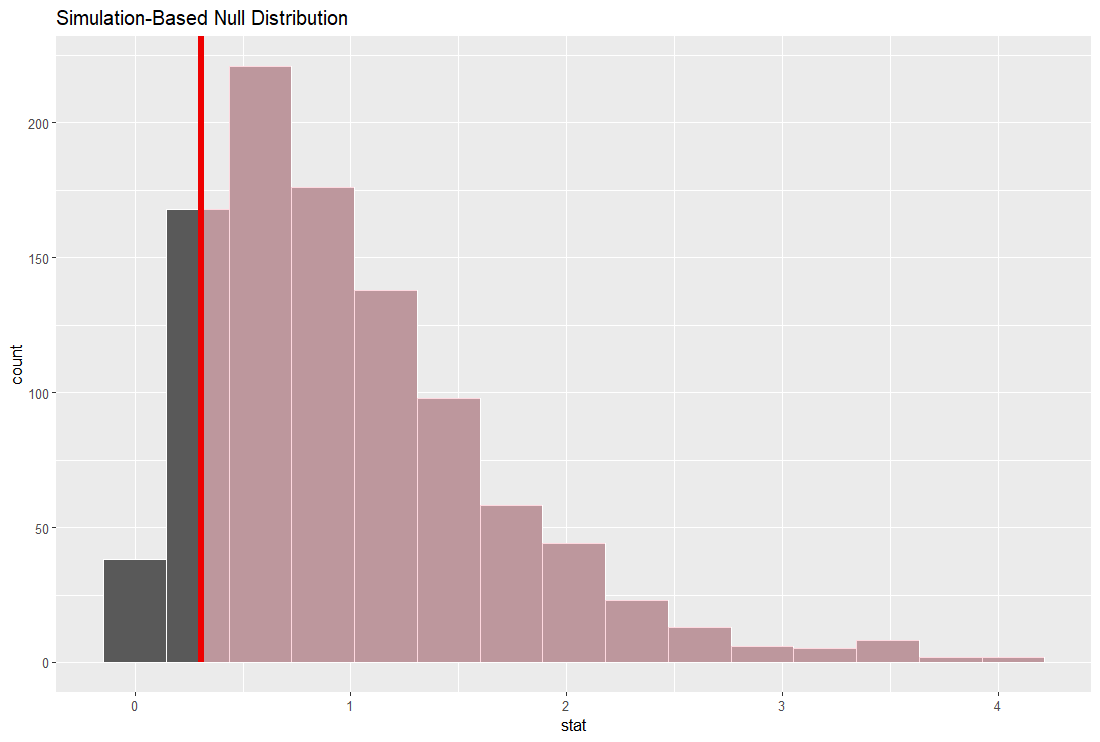
グラフにします。


赤い垂線の位置が実際に推計された係数の位置です。 l_num 以外は null distribution から離れていますので有意に 0 とは違うと思われます。

intercept, l_fuka, l_quantity の p 値は 0.05 よりもうんと小さいです。統計的に有意に 0 とは違うということですね。
bootstrap distribution を生成して、信頼区間を求めましょう。

信頼区間を求めます。

l_fuka と l_quantity は信頼区間が 0 を含んでいませんので、ここでも 0 とは有意に違うことが確認できます。 intercept は 0 を含んでいいますね。
グラフにしてみます。


l_fuka, l_quantity は 0 を含んでいないことがグラフでもわかります。
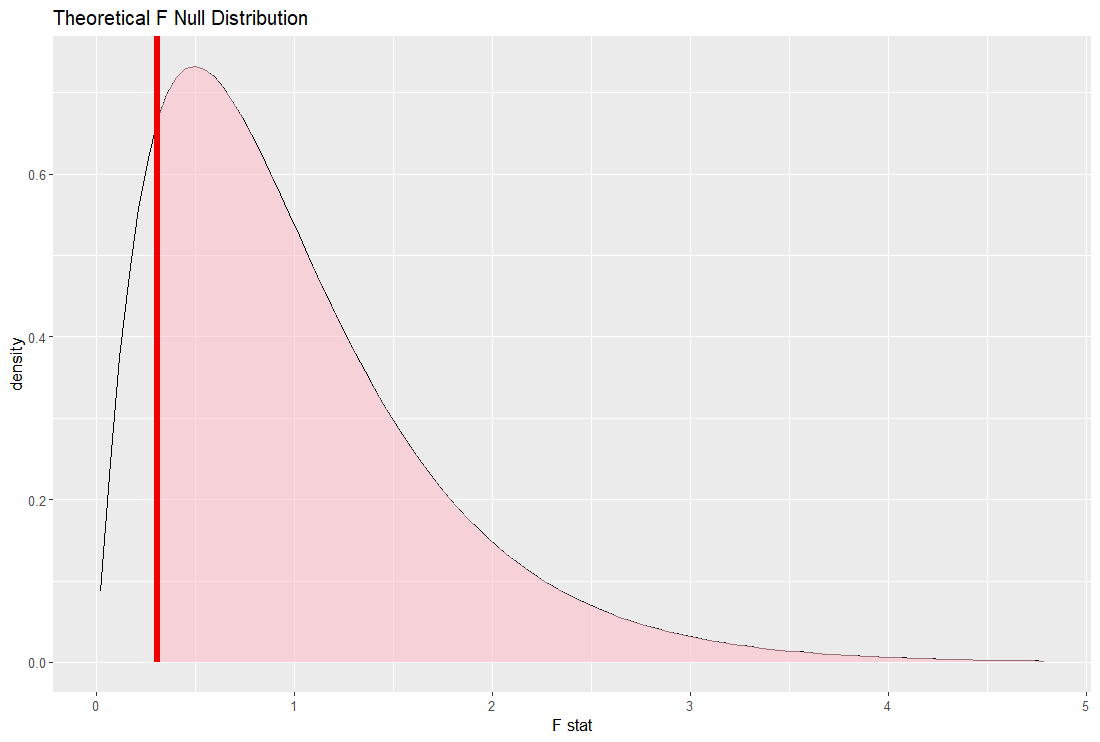
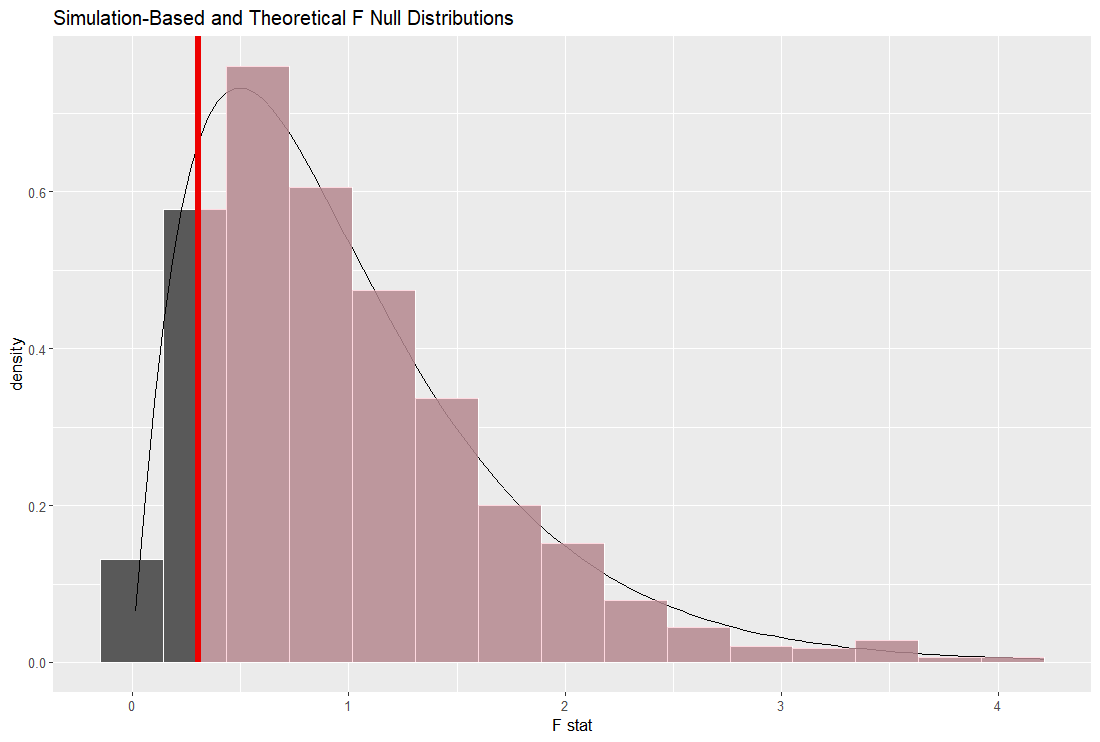
lm() 関数で理論ベースの重回帰分析もしてみます。

l_quality = 0.0061036 - 0.0008317 * l_num - 0.9973661 * l_quantity + 0.9977523 * l_fuka + u
という推計結果です。当然ですが、infer の fit() 関数での結果と同じです。
p 値も l_fuka, l_quantity は2.2e-16 なので 0 とほぼ同じですね。
信頼区間も同じような結果ですね。
l_quantity が大きいと、l_quality は下がる、l_fukaは大きいと l_quality は上がる、ということで、l_quality, l_quantity, l_fuka はみな対数変換値なので、他の変数の値が変わらなければ、quantity が 1% 上がると 1% quality は下がり、fuka が 1% 上がると quality は 1% 上がるということです。
今回は以上です。
次回は、
www.crosshyou.info
です。
初めから読むには、
www.crosshyou.info
です。