今回は社会保障費用統計データを使って、全体に対する比率を算出し、その増減をカテゴリカル変数にしてクロス表分析をしたいと思います。
まずは、CSVファイルに保存してあるデータをread.csv関数で呼び出し、summary関数をつかってどんなデータか見てみます。

全部の列が数値データで、2列目が総額で、3列目以降が総額の内訳です。
早速、総額に対する比率のデータを作ります。
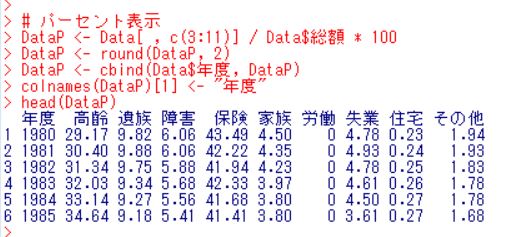
こうなります。この増減を計算するには、diff関数を使います。
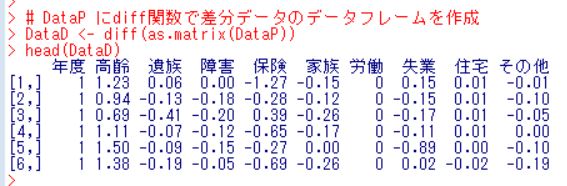
diff関数はデータフレームでは動かないようなので、まず、as.matrix(DataP)としてデータフレームをマトリックスに変換してからdiff関数を適用します。
高齢の1列目は、1.23ですが、これは1981年の30.40から1980年の29.17を引いた値です。1列目の年度の列はいらないので、削除して、行名を付与します。
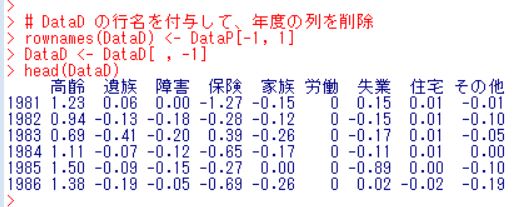
これで、0以上を"増加"、0未満を"減少"とカテゴリカル変数にしてみましょう。

まず、as.data.frame関数でマトリックスになっていたDataDをデータフレームに変換します。そして、ifelse関数で>=0のデータは、"増加"、そうでないデータは、"減少"に変換しています。そうして変換したデータをcbind関数で一つのデータフレームとしてまとめて、summary関数でそれぞれのデータ項目について増加、減少の度数を算出しています。
増加のほうが多いのは高齢と住宅のみで他の項目は減少のほうが多いです。
クロス表を作成してみます。table関数を使います。

高齢Cと遺族Cは関連があるのかどうか?フィッシャーの正確確率検定で確かめましょう。

p-value = 1 > 0.05 ですから、高齢Cと遺族Cは関連がない、という帰無仮説を棄却できません。
続いて、高齢Cと障害Cはどうでしょうか?

高齢が増加するときは障害が減少することが多く、高齢が減少するときは障害が増加するときが多いという関連性がありそうですが、フィッシャーの正確確率検定では、p-value = 0.1138 なので高齢と障害に関連性は無い、という帰無仮説を棄却するまでにはいたりませんでした。
高齢Cと保険Cはどうでしょうか?

p-value = 0.2169 > 0.05 ですから、高齢と保険には関連性は無い、という帰無仮説を棄却できません。
高齢と家族はどうでしょうか?

p-value = 0.4217 > 0.05 ですから、高齢と家族に関連性は無い、という帰無仮説を棄却できません。
高齢と労働はどうでしょうか?

p-value = 1 > 0.05 ですから、高齢と労働には関連性は無い、という帰無仮説を棄却できません。
高齢Cと失業Cはどうでしょうか?

p-value = 0.6478 > 0.05 ですから、高齢と失業には関連性は無い、という帰無仮説を棄却できません。
高齢Cと住宅Cはどうでしょうか?

p-value = 1 > 0.05 ですから、高齢と住宅に関連性は無い、という帰無仮説を棄却できません。
最後、高齢Cとその他Cはどうでしょうか?

p-value = 0.2357 > 0.05 ですから、高齢とその他には関連性は無い、という帰無仮説か棄却できませんでした。
以上の分析から、高齢の費用の比率の増減はそれ以外の項目の費用の比率の増減とは関連性が無い、ということがわかりました。