の続きです。
今回は、カテゴリ変数とカテゴリ変数の関係性をみてみましょう。
とはいってもこの産業別会社の財務営業比率のデータを見ますと、

カテゴリ変数は、「産業」だけです。カテゴリ変数はファクタなので、データの種類が<fct>となっています。
「年代」は<int>なので整数ですね。まずはこれをファクタに変換してしまいましょう。
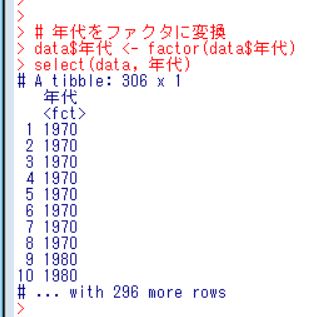
factor関数で整数のデータをファクタ(カテゴリ変数)に変換できます。
<fct>になっていますね。
カテゴリ変数とカテゴリ変数はtable関数でクロス表を作成できます。
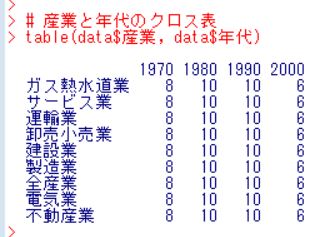
。。。まったく面白みのないクロス表ですね。。
何か、他の変数からファクタを作成することを考えましょう。
買掛金回転期間をsummary関数で処理すると、

このように、Median(中央値)がちょうど1.500なので、1.5未満を短回転、1.5以上を長回転と二分するカテゴリ変数を作ります。ifelse関数を使います。

dataはtibble形式のデータセットなので、ifelse関数で短回転と長回転の2つの値をとる変数を作成してもファクタにはならず、文字列<chr>になってしまいます。
そこで、factor関数で処理してファクタ<fct>にしました。
それでは、産業と回転のクロス表を作成してみましょう。
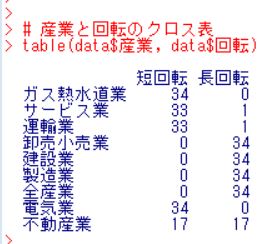
見事に産業ごとの特徴がでましたね。ガス熱水道業、サービス業、運輸業、電気業は短回転、卸売小売業、建設業、製造業、全産業は長回転、不動産業は半分半分です。
年代と回転ではどうでしょうか?

年代によって差があるようなないような。。。chisq.test関数でカイ自乗検定をじてみます。

p-value = 0.4174 > 0.05 なので、年代と回転に関連性があるとはいえません。
ここまでは、クロス表を作成して分析してきましたが、ggplot関数のgeom_count関数で視覚化できます。

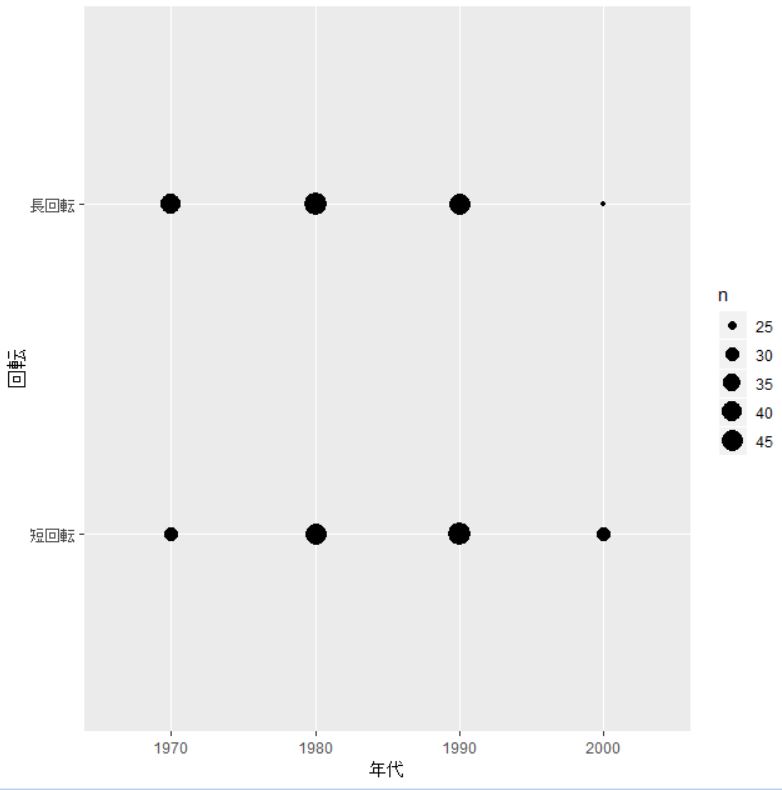
グラフの円の大きさが個数を表しています。
dplyパッケージのcount関数で個数を数えることもできます。

1行目は1970年代で短回転は30個、2行目は1970年代で長回転は42個と読めます。
ggplot関数のgeom_tile関数で視覚化できます。

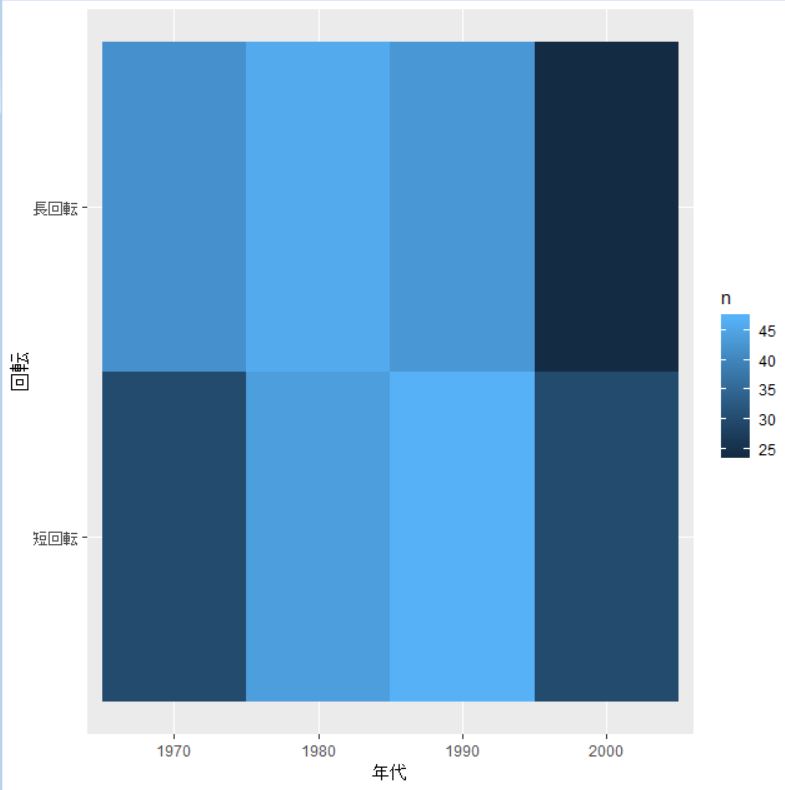
明るいタイルが個数が多く、暗いタイルが個数が少ないことを表しています。
今回は以上です。
次回は
です。