の続きです。
今回は、前回のブログで算出した「総計」に対する比率を使って「総計」の値を線形重回帰分析してみましょう。
lm関数を使うと簡単に実行できます。
総計 = α + β1 * 西暦 + β2 * R給与所得 + β3 * R事業所得合計 + β4 * R営業所得 + β5 * R不動産所得 + 誤差項
という回帰式ですね。

lm関数で線形重回帰分析のモデルを作成し、summary関数でモデルの結果を表示します。
一番下の行、F-statisticのp-valueが < 2.2e-16 なので、このモデルは統計的に有意です。
各係数を見ると、切片(Intercept)のp値は < 2e-16なので有意です。
西暦も < 2e-16なので有意ですね。係数が1.244e+06なので西暦が上がれば上がるほど、総計は上がる、ということですね。
給与所得のp値は0.06257 なので0.05より大きいので有意ではないです。
事業所得合計のp値は0.486306なのでこれも0.05より大きいので有意でないです。
営業所得のp値は0.00376なので0.05より小さく、有意です。係数がマイナスなので営業所得の割合が上がるほど、総計は減少する、ということです。
不動産所得のp値は1.54e-08なので0.05より小さく、有意です。これも営業所得と同じで係数がマイナスなので割合が上がるほど、総計は減少する、ということです。
下から2行目のAdjusted R-squaredの値が0.8948なのでかなりあてはまりはいいですね。
plot関数で残差をプロットしましょう。which = 1と指定すると、残差をプロットできます。

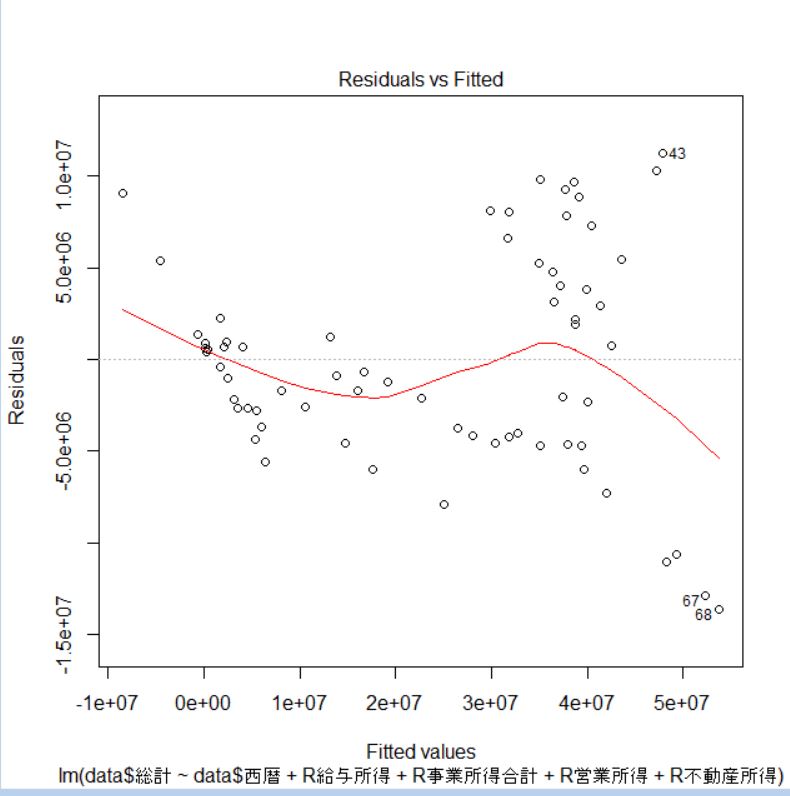
次に、有意でなかった給与所得と事業所得合計を除外したモデルを実行してみましょう。
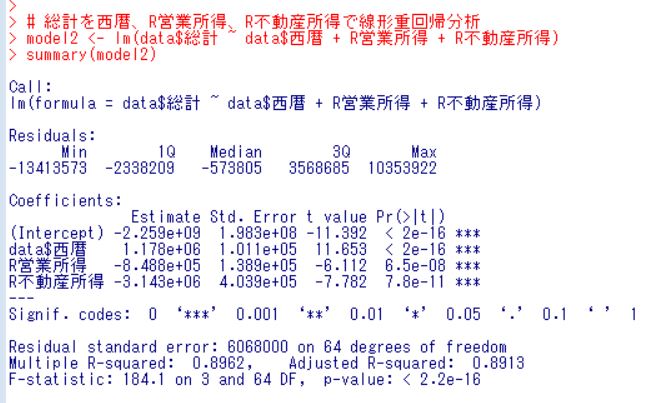
営業所得、不動産所得のp値がmodel1よりも小さくなりましたね。
残差をプロットします。

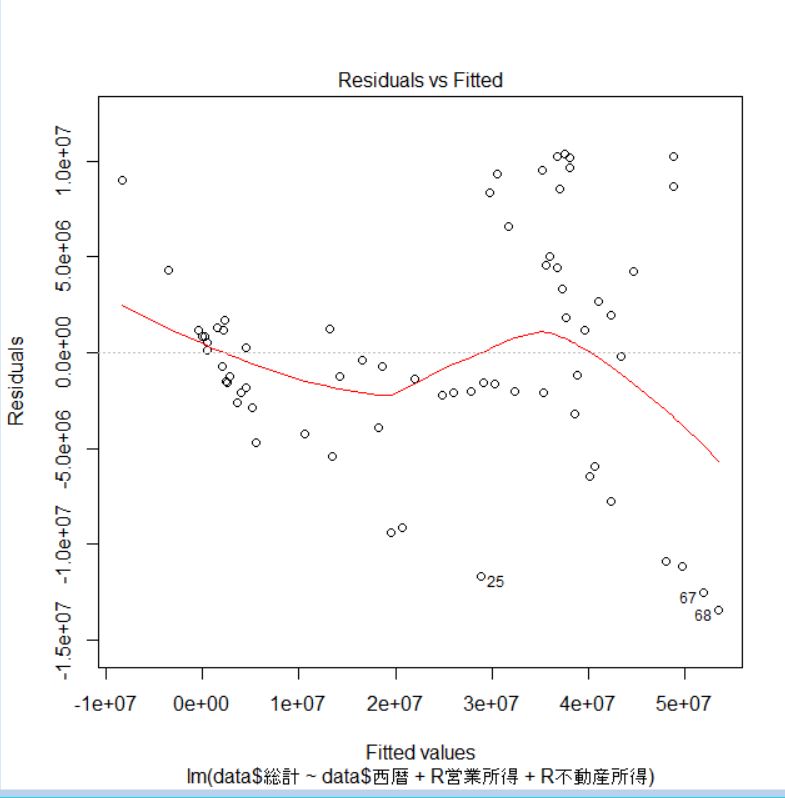
最後にanova関数を使ってmodel1とmodel2に違いがあるかどうかを確認しましょう。

p値が0.1348と0.05より大きいので、model1とmodel2に有意な違いはありません。なので、説明変数の少ないmodel2で総計を説明するには十分だということです。