の続きです。
今回は役員の人数と女性役員比率の関係をR言語で分析してみようと思います。役員の人数が多い会社ほど、女性役員を登用していると予想しているのですが、果たしてどうでしょうか?
まずは、男性役員数と女性役員数を合計して、「役員数」という変数を作成します。

最小値は3人、最大値は49人、平均値は11.19人、中央値は11人ですね。
hist関数でヒストグラム、density関数とplot関数でカーネル密度グラフ、sort関数とplot関数で小さい順グラフの基本3グラフを作成してデータの分布を視覚化しましょう。

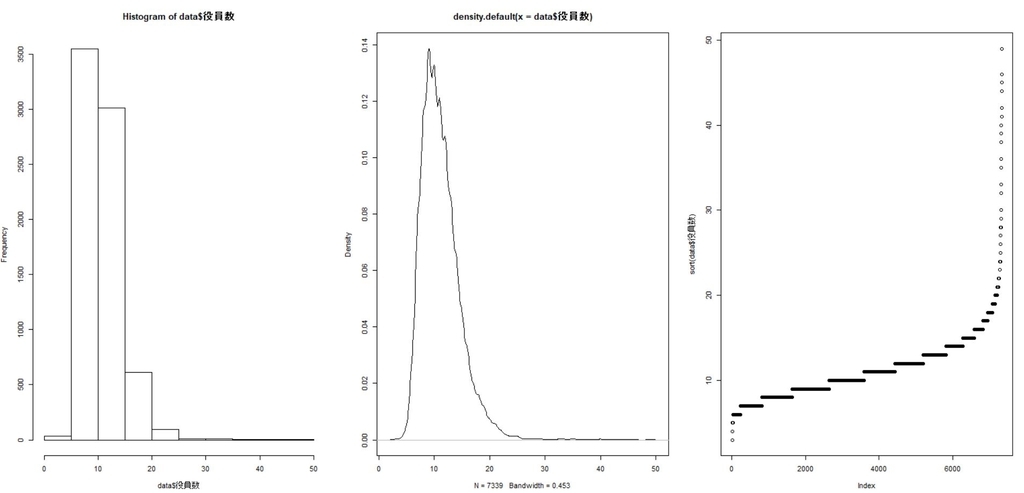
10人近辺が一番数が多いようですね。
20人以下のデータだけで、基本3グラフを描いてみましょう。
data$役員数[data$役員数 <= 20]とすると、20人以下のデータになります。

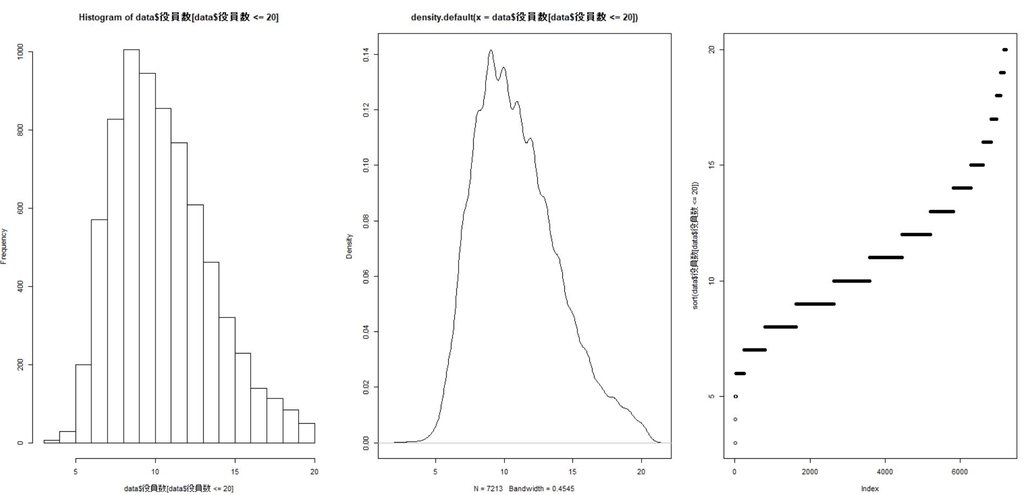
こうなりました。役員数を3つのグループに分類しましょう。
9人以下、10人から13人、14人以上にします。9人が第1分位値、13が第3分位値です。
cut関数でグループ分けできます。

9人以下の会社が2640社、10人から13人の会社が3176社、14人以上の会社が1523社です。
これで準備完了です。data$役員数グループとdata$wnonwのクロス表を作成してカイ自乗検定をします。
まずは、table関数でクロス表を作成します。

役員数の少ないグループは、女性役員がいない会社がいる会社の3倍くらいもあるのに対して、役員数の多いグループは女性役員がいない会社といる会社でそれほど数に違いがありません。やはり、はじめの予想(役員数の多い会社ほど女性役員の登用がある)どおりのようですね。prop.tableで比率を計算してみましょう。

役員数が少ないグループは女性役員のいる会社の割合は24.73%です。
中くらいのグループは32.81%です。多いグループは46.42%です。
xhisq.test関数でカイ自乗検定をしましょう。

p値が2.2e-16よりも小さいので、役員数と女性役員の有無は関連性が無いという帰無仮説は棄却されます。
つまり、役員数と女性役員の有無は関連がある、ということが分析できました。
調整済み残差を表示します。

調製済み残差は、絶対値で1.96より大きいセルが有意だということを表しますので、役員数が少ないグループは女性役員の無い会社が多く、役員数の多いグループは女性役員のいる会社が多いと解釈できます。
今回は以上です。
次回は
です。