の続きです。今回はR言語で各変数間の相関をみてみようと思います。
まず、cor関数で相関マトリックスを表示してみましょう。

MFRは男性の人数と女性の人数の比率
MFWRは男性の月額報酬と女性の月額報酬の比率
BORは賞与を支給した事業所の割合
MFBRは男性で賞与をもらった人数と女性で賞与をもらった人数の比率
MFBVRは男性の賞与額と女性の賞与額の比率です。
MFRとMFWRの相関が0.7069427で一番高く、MFRとBORの相関が-0.4908024で一番の逆相関です。
それぞれの変数の組み合わせの散布図をplot関数で作成しましょう。
まずは、MFR(男性の人数と女性の人数の比率)とMFWR(男性の月額報酬と女性の月額報酬の比率)です。

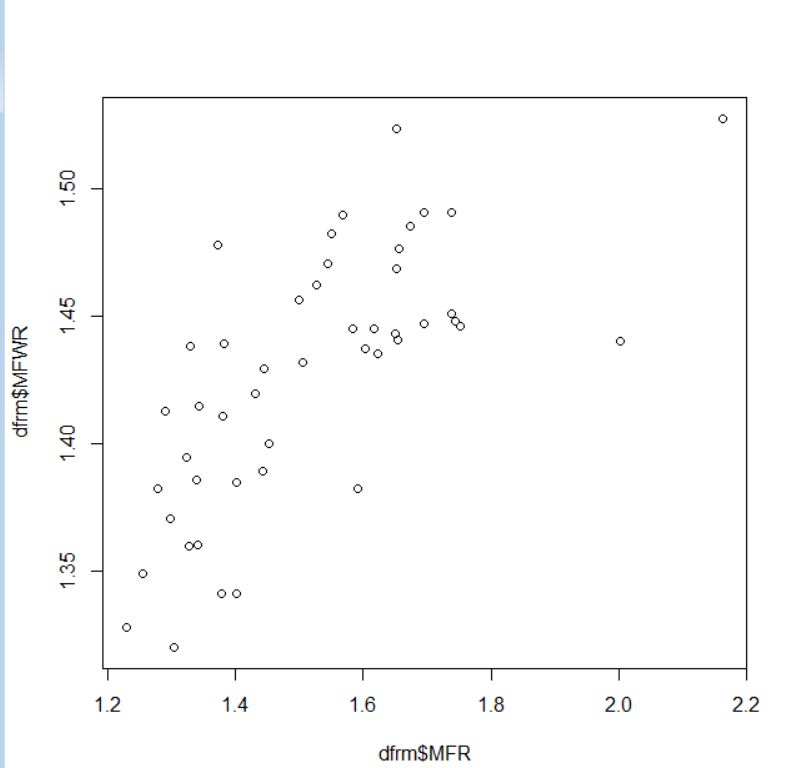
正の相関がありそうですね。cor.test関数で検定してみます。

p-value = 2.793e-08ですから0.05よりもp値は小さく、二つの変数の相関は有意だとわかります。男性比率高い&男性月額報酬高い、男性比率低い&男性月額報酬低いという相関関係です。
次は、MFR(男性の人数と女性の人数の比率)とBOR(賞与を支給した事業所の割合)です。

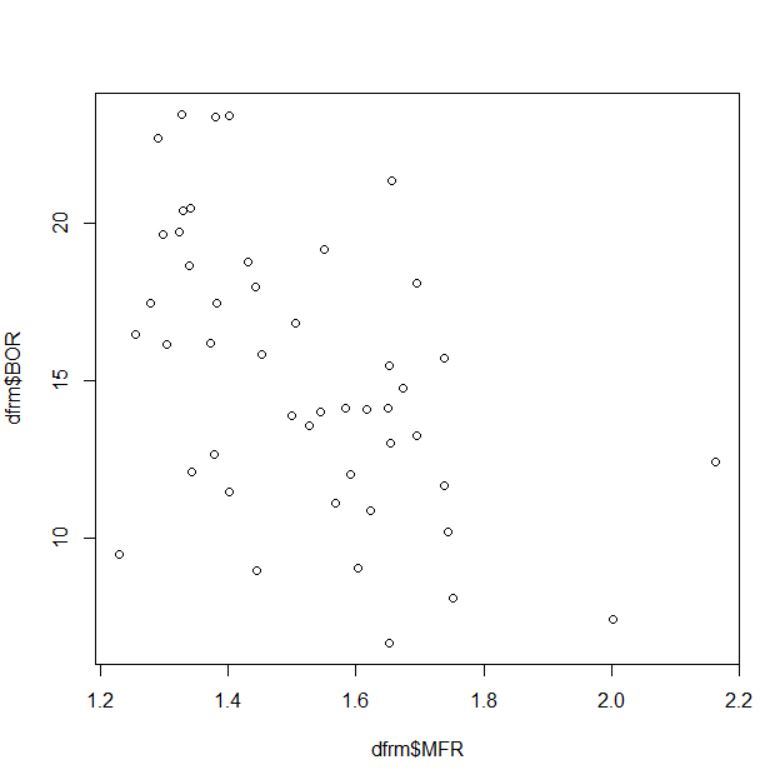
これもcor.test関数で相関の有意性を検定します。

p-value = 0.0004607と0.05よりも小さいので有意です。相関係数はマイナスですから、逆相関ですね。男性の比率が高い&賞与支給比率低い、男性比率低い&賞与支給率高いという相関関係ですね。
次は、MFR(男性の人数と女性の人数の比率)とMFBR(男性で賞与をもらった人数と女性で賞与をもらった人数の比率)です。

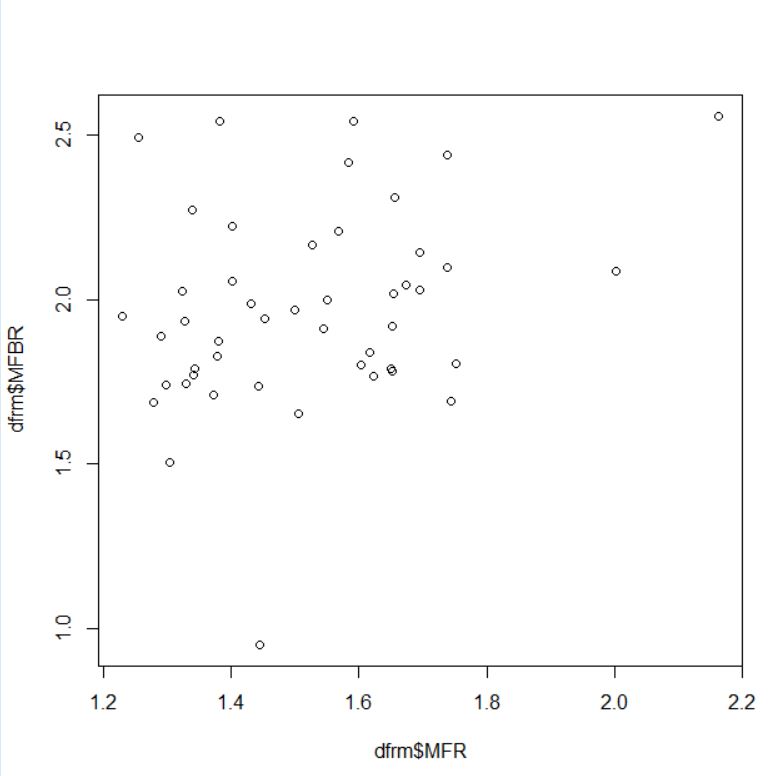
cor.test関数で有意性を検定します。

p-value = 0.05749となり、0.05よりも大きいですから相関は有意ではないということです。95 percent confidence intervalも-0.008811312から0.524218968と0をまたいでいますのでやっぱり相関関係は無いです。
MFR(男性の人数と女性の人数の比率)とMFBVR(男性の賞与額と女性の賞与額の比率)はどうでしょうか?

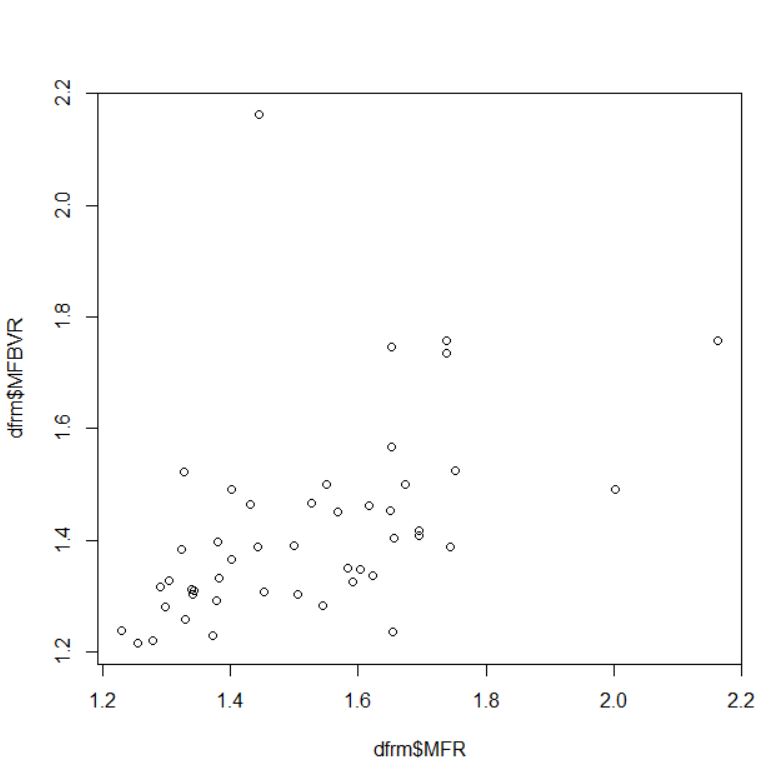
cor.test関数で有意性を検定します。

p-value = 0.0007273と0.05よりも小さい値ですから有意です。男性比率が高い&男性賞与が高い、男性比率が低い&男性賞与が低いという相関関係です。
MFWR(男性の月額報酬と女性の月額報酬の比率)とBOR(賞与を支給した事業所の割合)はどうでしょうか?

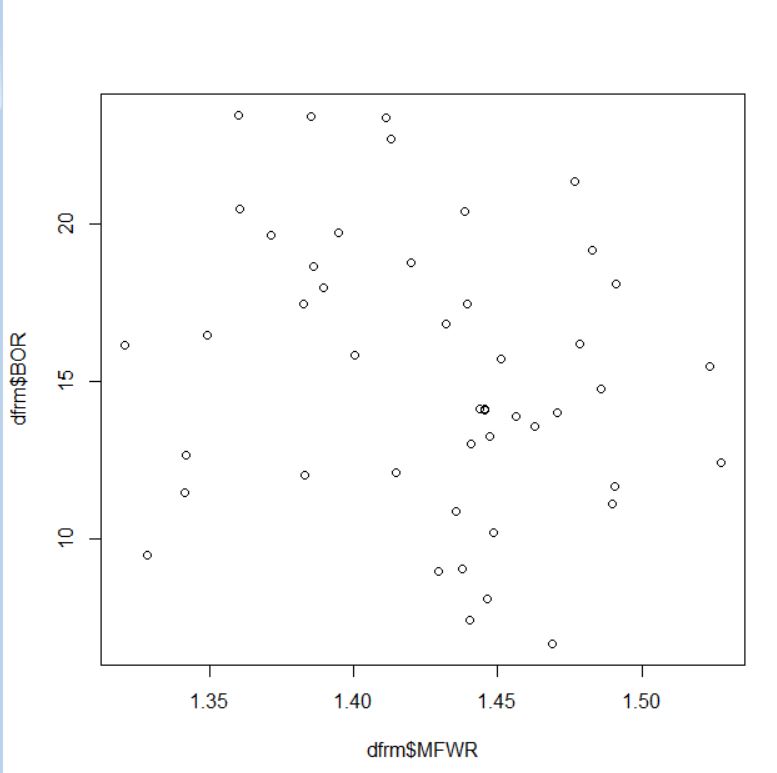
相関関係は無い感じですね。cor.test関数で有意性を検定します。

p-value = 0.1541です。相関性は無いですね。
MFWR(男性の月額報酬と女性の月額報酬の比率)とMFBR(男性の賞与支給人数と女性の賞与支給人数の比率)はどうなるでしょうか?

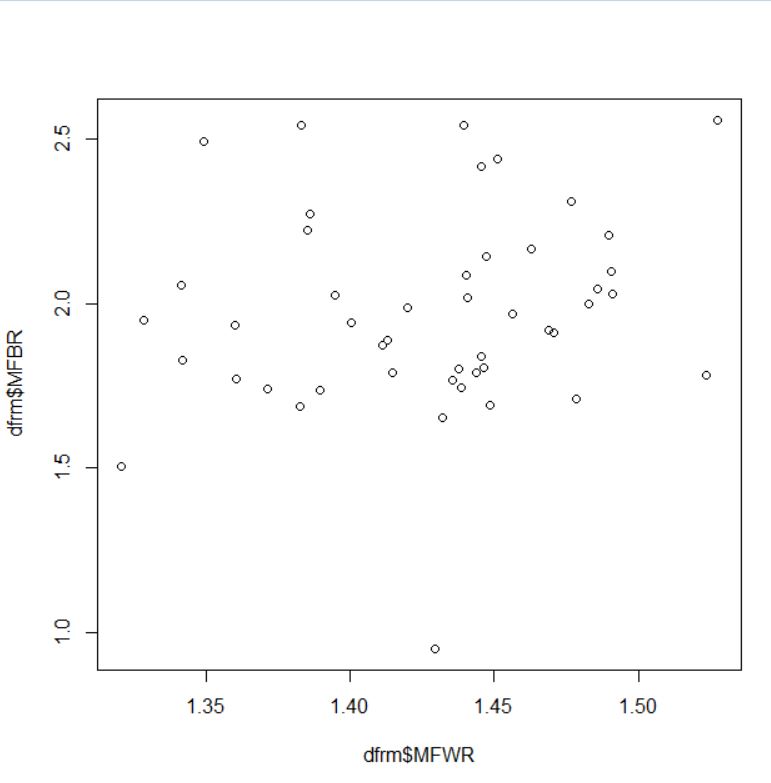
相関はなさそうですね。cor.test関数で検定します。

p-value = 0.3014ですので0.05よりも大きい値ですから相関は無いですね。
MFWR(男性の月額報酬と女性の月額報酬の比率)とMFBVR(男性の賞与額と女性の賞与額の比率)はどうでしょうか?

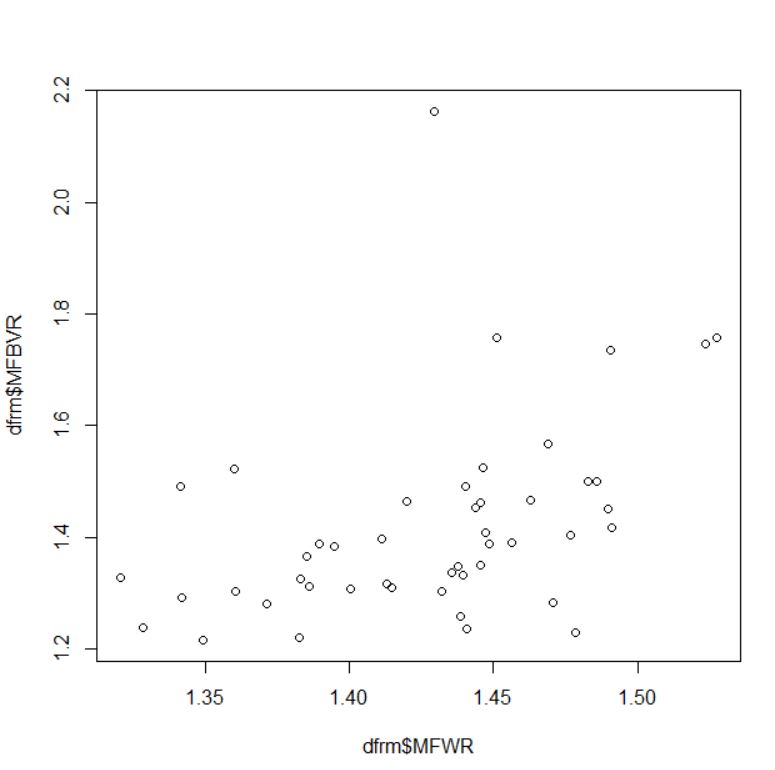
cor.test関数で有意性を検定します。

p-value = 0.002764と0.05よりも小さいので有意な相関関係です。男性の月額報酬高い&男性の賞与額高い、男性の月額報酬低い&男性の賞与額低いという相関関係です。
BOR(賞与を支給した事業所の割合)とMFBR(男性の賞与受取人数と女性の賞与受取人数の比率)の散布図を見てみます。

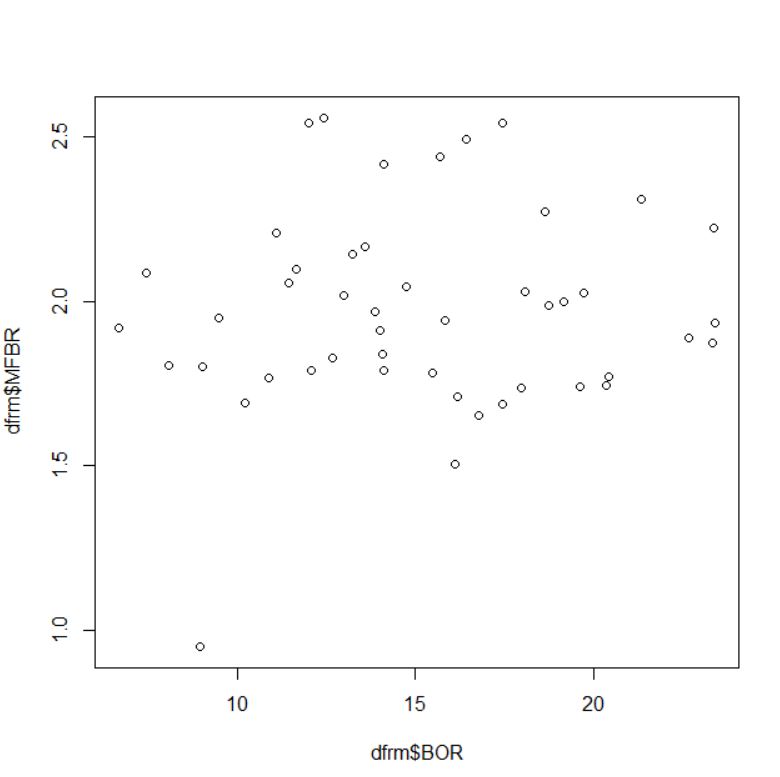
相関関係はなさそうですね。。cor.test関数で検定します。

p-value = 0.5255 です。0.05よりも大きな値です。相関関係は無いです。
続いてBOR(賞与を支給した事業所の割合)とMFBVR(男性の賞与額と女性の賞与額の比率)の散布図を見ます。

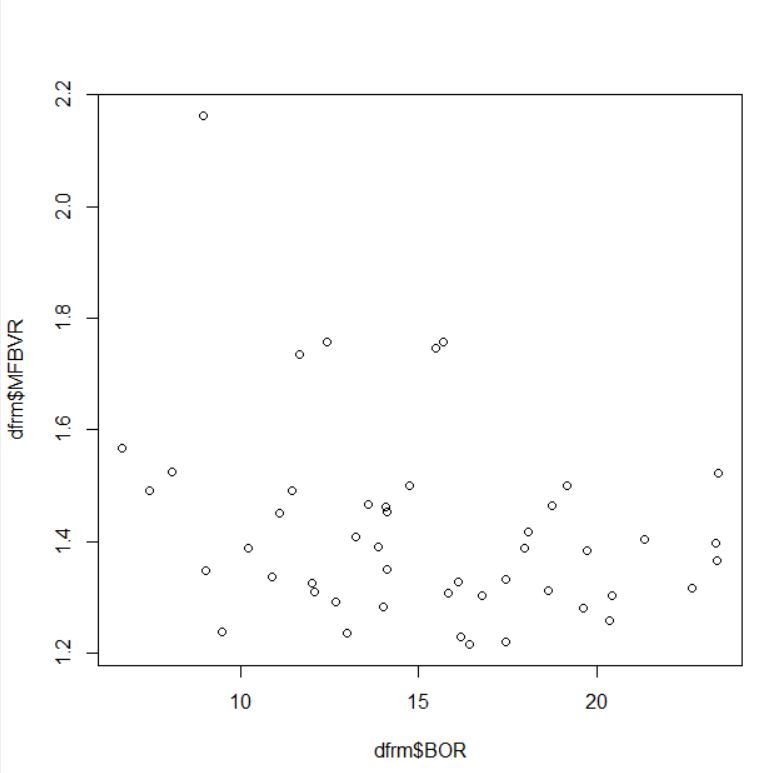
これも相関はなさそうです。cor.test関数で検定します。

p-value = 0.05459と0.05よりも大きな値ですので、相関に有意性は見られません。
最後の組み合わせ、MFBR(男性の賞与支給人数と女性の賞与支給人数の比率)とMFBVR(男性の賞与額と女性の賞与額の比率)を見ましょう。

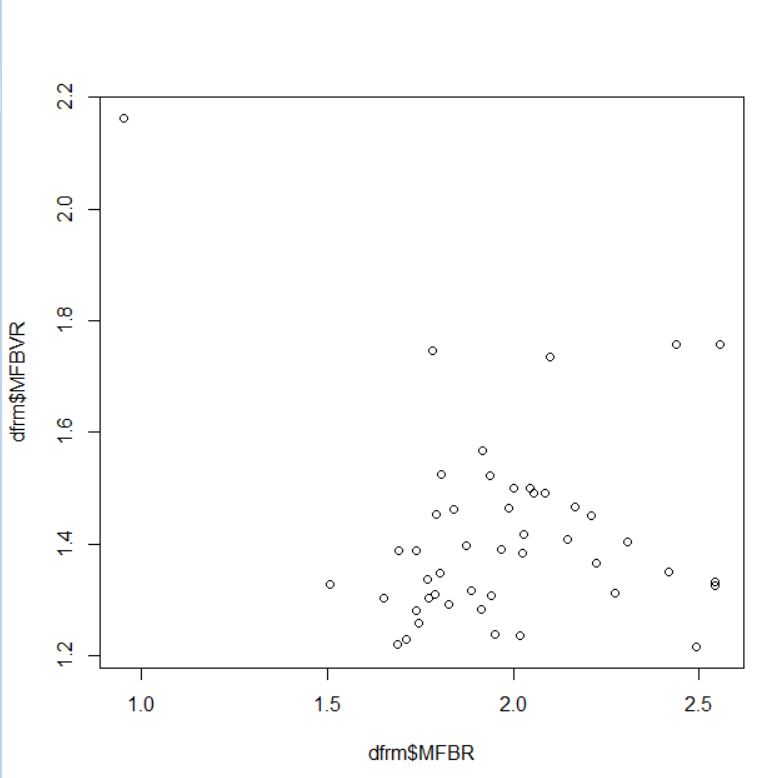
散布図の左上にプロットがあります。これを除くと相関は無い感じですね。cor.test関数で検定しましょう。

p-value = 0.3544ですので0.05より大きいです。相関関係は有意でないです。
以上整理すると、有意な相関関係があると認められたのは、
MFR(男性の人数と女性の人数の比率)とMFWR(男性の月額報酬と女性の月額報酬の比率)(プラス相関)
MFRとBOR(賞与を支給した事業所の割合)(マイナス相関)
MFRとMFBVR(男性の賞与額と女性の賞与額の比率)(プラス相関)
MFWR(男性の賞与支給人数と女性の賞与支給人数の比率)とMFBVR(プラス相関)の4組でした。
今回は以上です。
次回は
です。