今回は消防機関の出動回数のデータを分析しようと思います。
消防機関の出動回数の定義は

です。
www.e-stat.go.jpにありました。
政府統計の総合窓口(e-Stat)からデータを取得して、下のようなCSVファイルにしました。
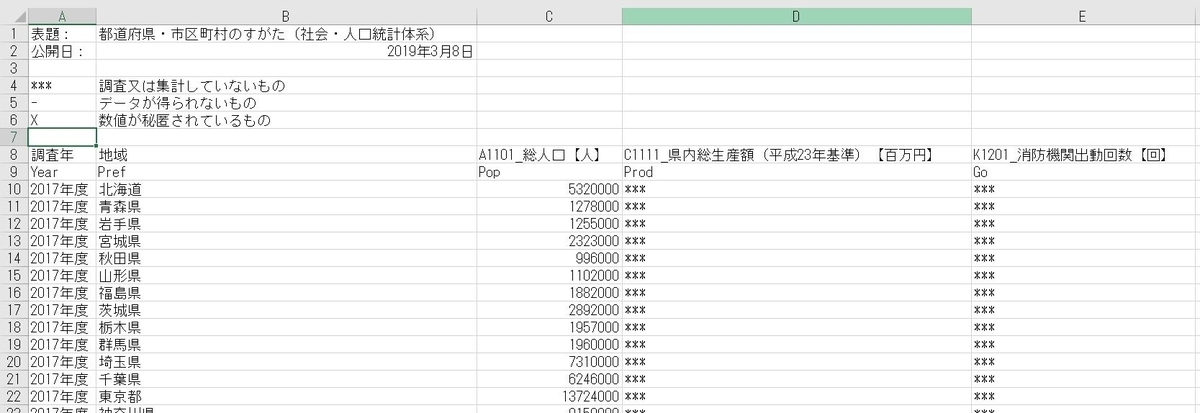
出動回数だけなく、人口と生産額のデータも同時に取得しています。
これを、R言語で読み込んで、分析をします。
まずは、read.csv関数でデータを読込みます。

2021の観測と5つの変数です。Yearは年度、Prefは都道府県、Popは人口(人)、Prodは生産額(百万円)、そして、Goが消防機関の出動回数です。消防機関の出動回数って年間でどのくらいなんでしょうね。
まずは、NAの行をna.omit関数で削除して、summary関数で各変数の基本的な統計値を確認しましょう。

Prefのところに注目すると、各都道府県は10個ずつあります。つまり、10年間のデータということですね。2006年度から2015年度ということですね。
人口(Pop)の最小値は57万3441人です。今朝のニュースで、2018年の日本全体の人口減少が44万人とありましたね。最小人口の県の人口が57万人ということは1年でこの県のほとんどの人口が減ってしまったということですね。そう考えると日本の人口減少ってすごいですね。
生産額(Prod)は数が大きすぎて実感がわかないですが、平均が11兆円ほどです。トヨタの売上高って30兆円ですよね。こう考えると、トヨタって凄いですね。
そして、消防機関の出動回数(Go)は、最小で9814回、最大で52万3487回です。1日当りに直してみます。

1日当りになおすと、最小で27回、最大で1400回ほどです。
今回は、
1.消防機関の出動回数は年度で減少傾向なのか増加傾向なのか?
2.人口当りの出動回数の多い・少ない都道府県はどこか?
3.生産額当りの出動回数の多い・少ない都道府県はどこか?
4.出動回数を人口を生産額で回帰分析してみる。
の4点を調べてみようと思います。
まずは、年度ごとの出動回数の合計値を算出してみます。tapply関数ですね。

2006年度は354万件で2015年度は373万件なので、微妙に増えている感じです。barplot関数で棒グラフにしてみます。
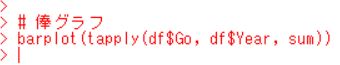
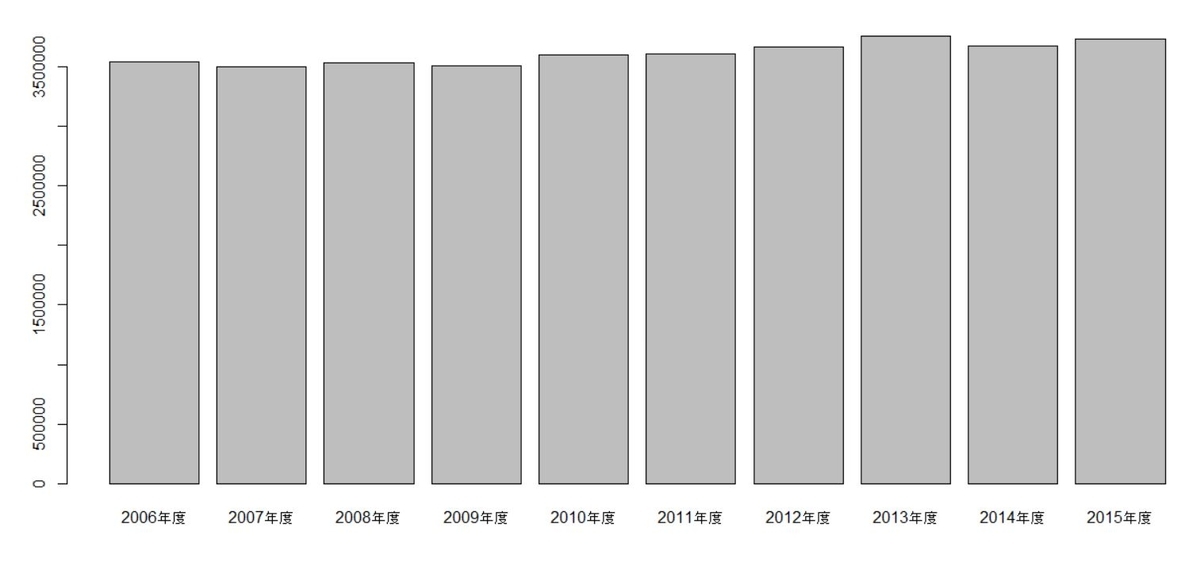
グラフで見ると変わらない感じですね。
各年度をZスコアに換算してみましょう。scale関数です。
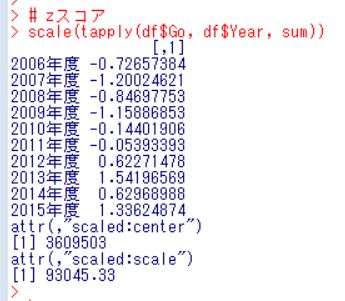
2015年度は平均値から1.33標準偏差大きいということですね。明らかに2015年度の出動回数は多かった、というレベルではないですね。
次は、人口当たりの出動回数を見てみましょう。

order関数、rev関数、head関数を使って上位の都道府県を表示しました。2007年度の群馬県が一番です。0.082回です。1000人当り82回です。群馬の次は、北海道と岩手県が上位です。
少ないところはどこでしょうか?
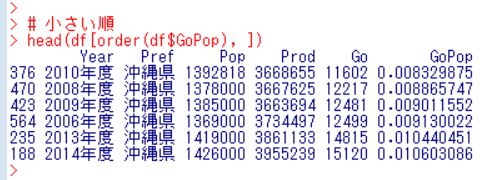
沖縄が上位を独占です。2010年度は、消防機関の出動回数は1000人当り8回しかありませんでした。群馬県の10分の1ですね。
生産額当りの出動件数も同様にやってみます。

一番多かったのは2007年度の群馬県です。百万円当り0.02回、1億円当り2回です。
一番少ないのは沖縄県で、2010年度の沖縄県は、1億円あたり0.3回です。
10年間の平均値のデータフレームを作って、それでもう一度、多い順、少ない順を表示してみましょう。
まず、aggregate関数で10年間の平均値のデータフレームを作ります。
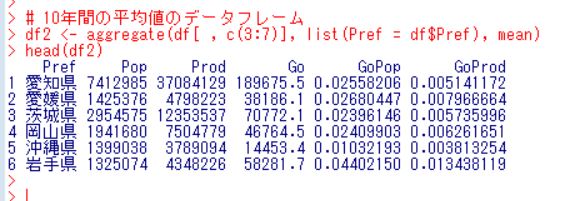
GoPopの大きい順、小さい順を表示します。

出動回数の多いのは岩手県、北海道、青森県、京都府、島根県、東京都です。少ないのは、沖縄県、佐賀県、徳島県、香川県、宮崎県、埼玉県です。
GoPord(生産額当りの出動回数)も同じようにみてみましょう。

生産額当りの出動回数の多いのは岩手県、北海道、青森県、長崎県、島根県、秋田県でした。少ないのは沖縄県、徳島県、佐賀県、香川県、東京都、三重県でした。
沖縄県は消防機関の出動回数の少ない県といえますね。
それでは、次は、出動回数を人口と生産額で回帰分析してみましょう。
データフレームは、10年間の平均のdf2のほうを使いました。
まずは、出動回数(Go)と人口(Pop)、生産額の散布図をみてみましょうか?pairs関数を使います。

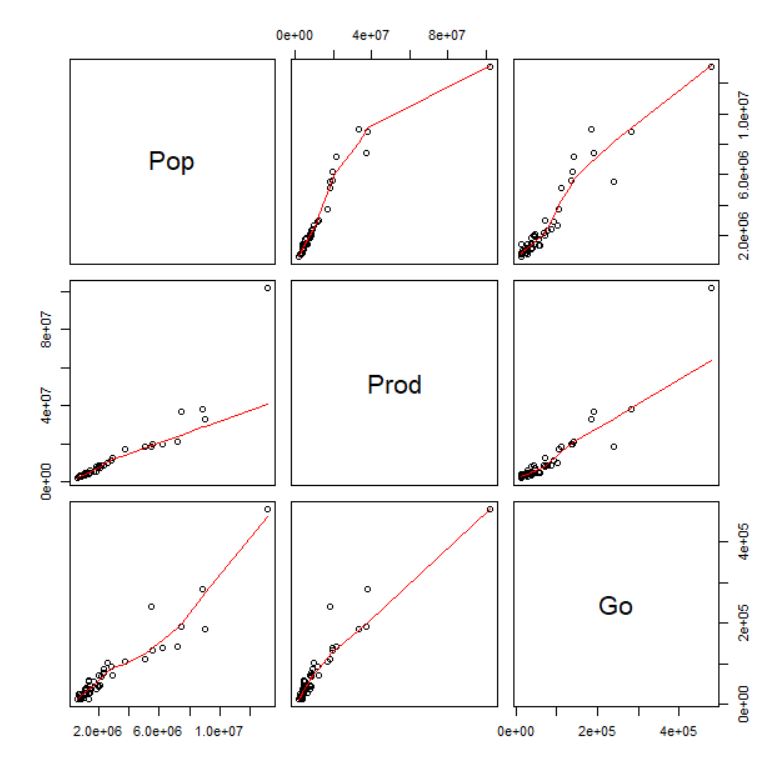
3段目の二つの散布図がY軸がGoの散布図です。Pop, Prodともに正の相関ですね。
Pop, Prod, Goの3つとも小さい値の観測と大きい値の観測の差が大きいので、3つとも対数をとりましょう。

これでもう一度散布図を描いてみます。

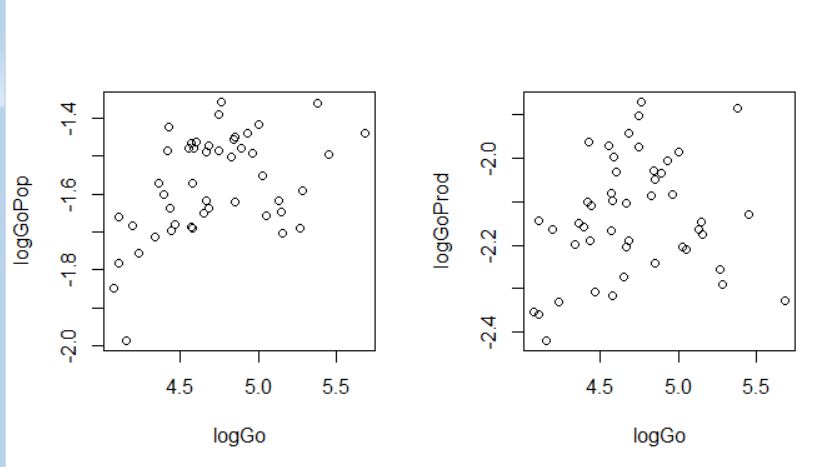
こうして2つの散布図を見ると、人口のほうが生産額よりも出動回数に関係しているようです。
それでは、lm関数で回帰分析をしてみます。
まずは、人口(logPop)と生産額(logProd)の2乗項と交差項の入ったフルモデルを考えます。
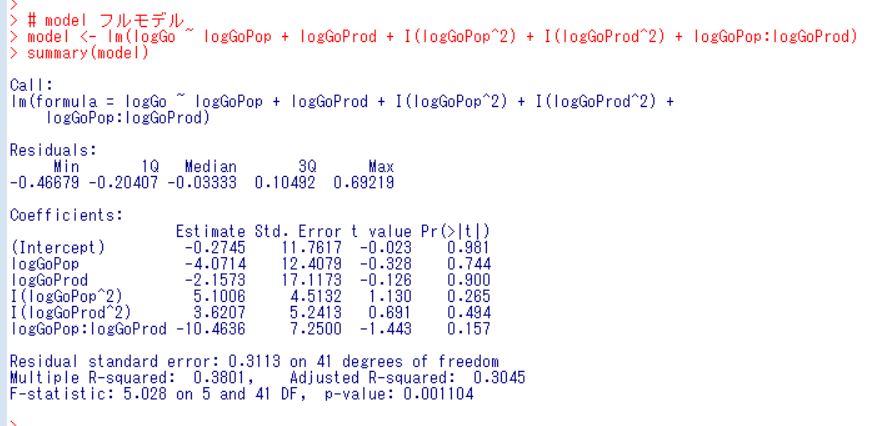
p-value = 0.001104と0.05以下なので、このモデルは有意です。が、どの変数の係数も有意ではないですね。。。こんなこともあるのですね。
まずは、交差項を削除したmodel2を考えます。

p-value = 0.001025なので有意なモデルです。anova関数でmodelとmodel2を比較します。有意な違いが無ければ、説明変数の少ないmodel2を採用します。

p値が0.1565なので0.05よりも大きいですから、modelとmodel2に有意な違いがあるとは言えません。なので、説明変数の少ないmodel2を採用します。さらにp値が一番大きかったlogGoPopの2乗項を削除したmodel3を考えましょう。

p-value = 0.0003308なので有意なモデルです。anova関数でmodel2とmodel3を比較します。
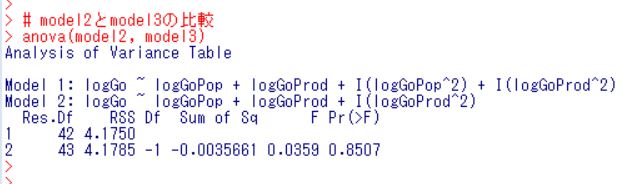
p値が0.8507なのでmodel2とmodel3には有意な違いはありません。よって変数の少ないmodel3を採用します。
model3からさらにlogGoProdの2乗項を削除したmodel4を考えましょう。
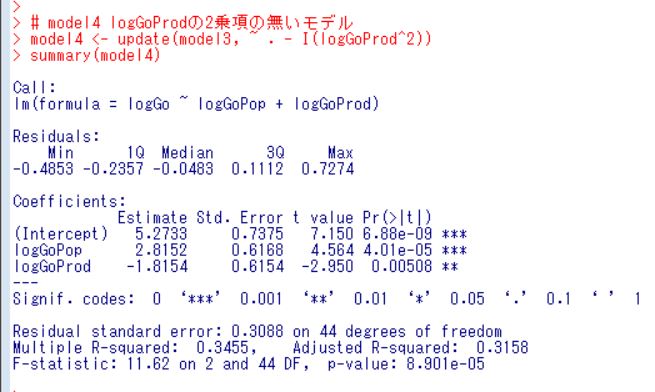
p-value = 8.901e-05なので有意なモデルです。そしてこのmodel4で初めてすべての変数のp値が0.05以下で有意になりました。
logGoProdのほうがp値が大きいのでこっちを削除したmodel5を考えましょう。
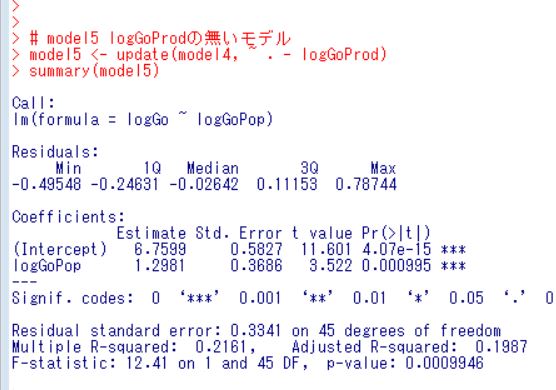
p-valueは0.0009946なので有意です。anova関数でmodel4とmodel5を比較しましょう。

p値が0.005075と0.05よりも小さいので、model4とmodel5は有意に違う、ということです。model5は変数を削除しすぎということですね。
なので、model4が一番いい回帰モデルです。
もういちどサマリー画面を出します。
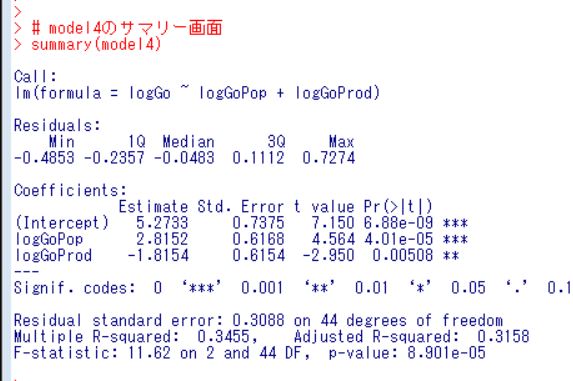
logGoPopの係数の符号はプラスです。つまり、生産額が同じなら人口が多いほど出動回数は増えるということですね。
logGoProdの係数の符号はマイナスです。つまり、人口が同じなら生産額が多いほど出動回数は減るということですね。生産額が多いということはそれだけ災害に対する備えもしっかりしていて出動しなくても大丈夫なケースが多いということかな?
今回は以上です。