の続きです。
今回は、大企業、中堅企業、中小企業という企業規模の違い、Scaleをexplanatory variableにしてANOVAをしてみます。企業規模の違いで短観の数値に違いはあるでしょうか?
まずは、グラフで様子を確認しましょう。
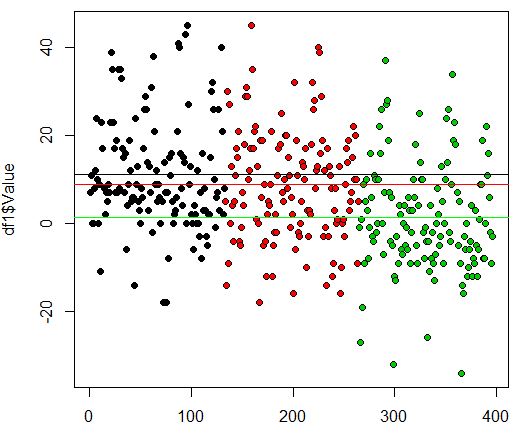
黒い点が大企業で黒い水平線が大企業の平均値。
赤い点が中堅企業で赤い水平線が中堅企業の平均値。
緑の点が中小企業で緑の水平線が中小企業の平均値です。
企業規模が小さいほど短観の値は悪くなっています。
tapply関数でそれぞれの平均値を計算します。

大企業が11.07, 中堅企業は8.82, 中小企業は1.42と中小企業は極端に低いですね。
今回はtapplyの結果をkiboというベクトルに保存しました。なぜかというと、あとて、kibo[1]で大企業の平均値、kibo[2]で中堅企業の平均値、kibo[3]で中小企業の平均値として使うためです。

ついでに、df1$Scale == "大企業", df1$Scale == "中堅企業”, df1$Scale == "中小企業"もベクトルにしておいてあとで、SSEの計算で使います。

SSY, the sum of the squares of the differences between the y values and the allovermean を計算します。
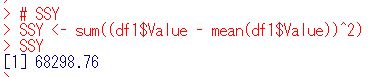
SSY, 毎回計算していますが、本当は1回計算すればいいです。でもこれは練習ブログなので毎回計算して、毎回同じ68298.76を得ています。
SSE, the error sum of squaresを計算します。ここでさきほど作った、kibo, idxL, idxM, idxSが活躍します。

どうでしょう。前回はそれぞれのファクタのSSEを計算して最後に合計しましたが、今回はいちどにSSEを計算しました。わかりやすい式だと思います。SSEは61578.27です。
SSAはSSYからSSEを引いた値です。

SSAは6720.49です。SSAのDegrees of freedom, 自由度は2です。なのでSSAのMean squareは、
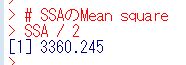
3360.245です。
SSEの自由度は、SSYの自由度が395で、SSAの自由度が2ですから、395 - 2 = 393です。SSEのMean squareは、
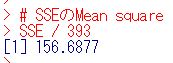
156.6877です。なので、F ratioは3360.245 / 156.6877です。

21.44549です。
これでANOVA表の構成要素は全部計算しました。
まとめましょう。
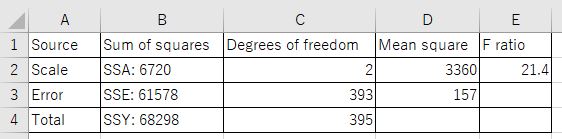
F ratioの21.4という値が偶然に起こりえる値なのか、それとも企業規模に違いが無いと怒らない値なのか、qf関数でチェックします。

3.02よりも21.4は大きいですから企業規模の違いは短観の値に影響があるといえます。
pf関数でp値も求めます。

1.446713e-09です。0.05よりも小さい値です。
aov関数とsummary関数でいままでの答え合わせをします。

p値もpf関数で計算した値と同じだし、ANOVA表ともSum of squaresやMean square, F ratioが一緒です。
今回は以上です。
企業規模は短観の数値と関係し、規模が小さくなるほど短観の値は低くなっています。