の続きです。
今回は、Michael J. CrawleyのStatistics: An Introduction Using Rを参考にして、日経平均、ドル円、売買代金の月次変化率の平均値の標準誤差と信頼区間を求めてみようと思います。

Statistics: An Introduction Using R
- 作者:Michael J. Crawley
- 出版社/メーカー: Wiley
- 発売日: 2014/11/24
- メディア: ペーパーバック
上の画像のような本です。データのCSVファイルをウェブからダウンロードできるので実際にR言語を使って自習できます。
variance(分散)はvar関数で取得できます。

日経平均の前月比のvarianceは0.001445938、ドル円の前月比のvarianceは0.0003694305、売買代金の前月比のvarianceは0.01295124です。売買代金のvarianceが一番大きいですね。
これらのvarianceが統計的に有意に違うのかどうか、var.test関数で調べてみましょう。
日経平均とドル円のvarianceを比較します。

p-value = 5.962e-07と0.05よりも小さい値なので、日経平均の前月比のvarianceとドル円の前月比のvarianceは有意に違いがあることがわかります。ということは、売買代金の前月比のvarianceは他の二つとはもっと離れていますから、それぞれのvarianceは有意に違うのですね。
それでは標準誤差(standard error)を計算しましょう。
標準誤差 = SQRT(variance / n)です。nはデータの数です。

length(df$ChgNikkei) - 1 と1を引いているには、NAが一つあるからですね。
それぞれの平均値も計算しましょう。mean関数です。

Chgのデータ数(NAを除いた数) を数えましょう。length関数とis.na関数とsum関数を使うと計算できます。
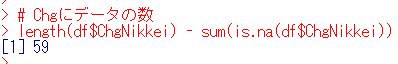
データの数は59個ですね。
標準誤差と平均値とデータの個数を使ってこのように記述することができます。
日経平均の月次変化率の平均値は、1.005526 ± 0.004950497(1 s.e., n = 59)
ドル円の月次変化率の平均値は、0.9985149 ± 0.002502306(1 s.e., n = 59)
売買代金の月次変化率の平均値は、1.006599 ± 0.01481595(1 s.e., n = 59)
なんか学術論文っぽいですね。笑
プラスマイナスだと、いまいちイメージがつかめないので、実際に範囲を計算してみます。
まず、マトリックスを作成しました。

これで三つを一度に計算できます。

日経平均は平均値 - 1標準偏差の値が1.0005754と1よりも大きいですので、分析期間中は上昇傾向だったのかもしれないですね。ドル円と売買代金は 1をまたいでいますから分析期間では上昇傾向でも下降傾向でもなかったということですね。
信頼区間も計算します。
n = 59ですから自由度は59 -1 = 58 です。95%の信頼区間は、qt関数を使って、qt(0.025, 58)、qt(0.975, 58)を標準誤差にかけた値になります。

95%の信頼区間(n = 59)では、日経平均の月次変化率の平均値は、0.9956164から1.015435の範囲になり、1.0をまたぎますので、上昇傾向、下降傾向、どちらともいえないですね。
マトリックスでは、mtx[ , "AVG"]のように列名で指定することもできます。
今回は以上です。