の続きです。
いままで、YearMonthを無視して分析してきましたので、今回は年によって日経平均の月次変化に違いがあるかどうか、ANOVA分析をしてみたいと思います。
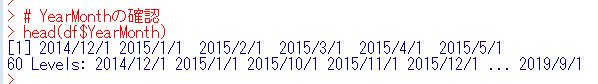
head関数ではじめの数データを表示してみました。左から4文字が年ですね。
この4文字を取り出します。
substr関数ではじめの4文字を取り出します。
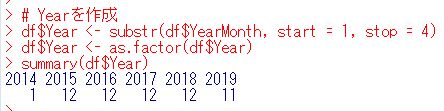
2014年はデータが一つですので、分析は無視します。
まず、YearとChgNikkeiだけの作業用のデータフレームを作ります。
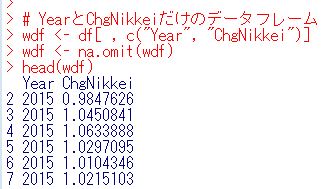
NAのある行をna.omit関数で削除したら、2014年はなくなりましたね。tapply関数でYearごとの平均値を出します。
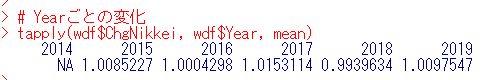
2014年がNAで表示されています。ファクタの水準としてはまだ残っているのですね。整理します。
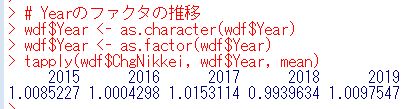
as.character関数で文字列に戻し、as.factor関数でファクタにまた戻しています。
これで、2014はなくなりました。2018年が0.9939634で一番低く、2019年が1.0097547で一番高いです。
Michael J. CrawleyのStatistics: An Introduction using Rを参考にしてANOVA分析します。

Statistics: An Introduction Using R
- 作者:Michael J. Crawley
- 出版社/メーカー: Wiley
- 発売日: 2014/11/24
- メディア: ペーパーバック
aov関数でANOVA分析ができます。
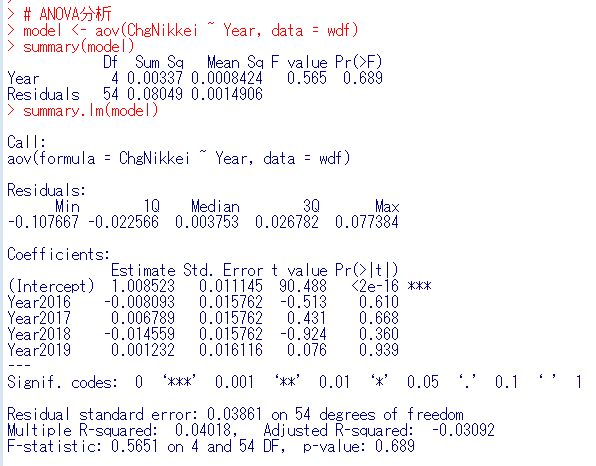
aov関数でANOVA分析のモデルオブジェクトを作り、summary関数、summary.lm関数で分析結果を表示します。
p値は0.689ですから結論は年ごとの違いがあるとは言えない、となりました。
棒グラフを描いてみます。barplot関数です。

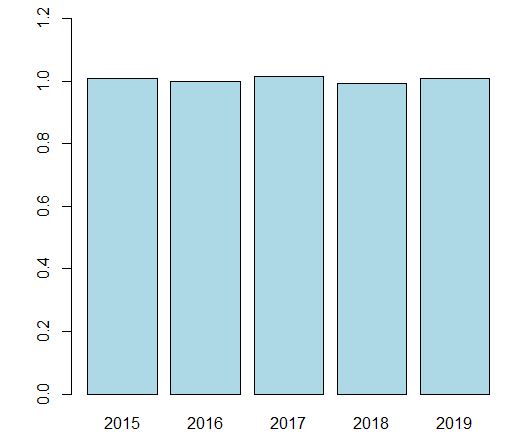
この棒グラフにstandard error(標準誤差)を追加します。
まず、er_barsという関数を作成します。
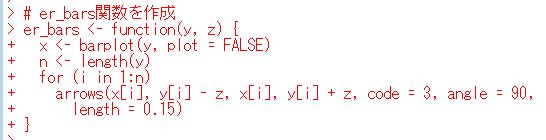
yが棒グラフのもとのデータ、zが標準誤差、standard errorですね。xは棒グラフのx軸になります。
標準誤差(standard error)はさっきのsummary.lm関数の結果ありましたね。
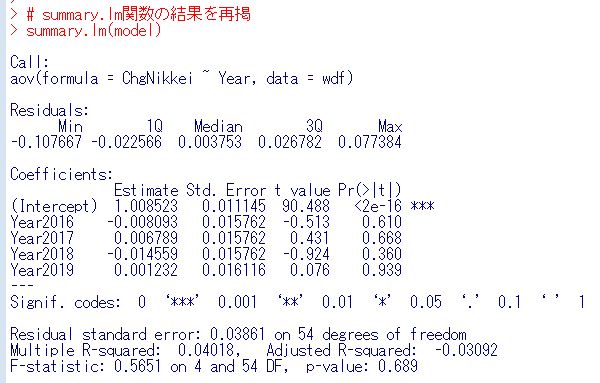
2016年から2018年は0.015762で2019年は0.016116です。

これで、er_bars関数を使えます、yがheight, zがseです。

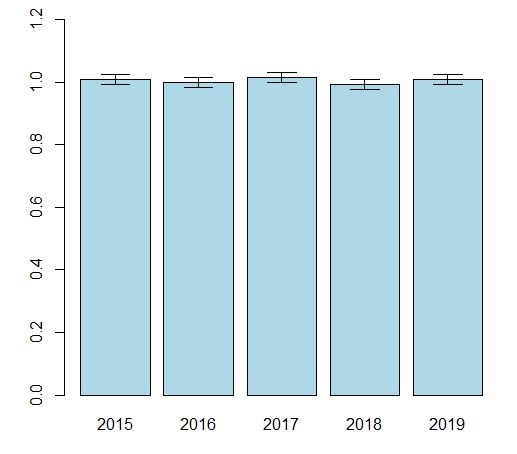
上手く標準誤差も棒グラフ上に表示できました。
95%の信頼区間を表示してみましょう。
まず、信頼区間のベクトルを作成します。2015年から2018年はデータ数は12個ですから、自由度は11、2019年はデータ数は11個ですから自由度は10です。

こうして信頼区間のベクトルができたので棒グラフと信頼区間を表示しましょう。

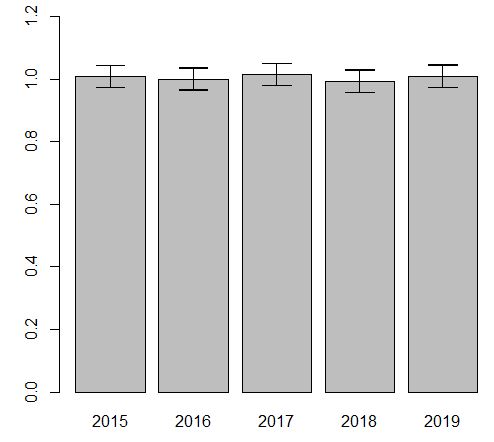
はい。できました。各棒グラフの信頼区間が重なっていますから、各棒グラフに有意な違いは無いことが目で見てわかりますね。
今回は以上です。