の続きです。
今回は、現状と先行きで回帰分析をしてみようと思います。
先行きを反応変数、現状を説明変数にしてみます。
まずは、plot関数で散布図を描いてみましょう。

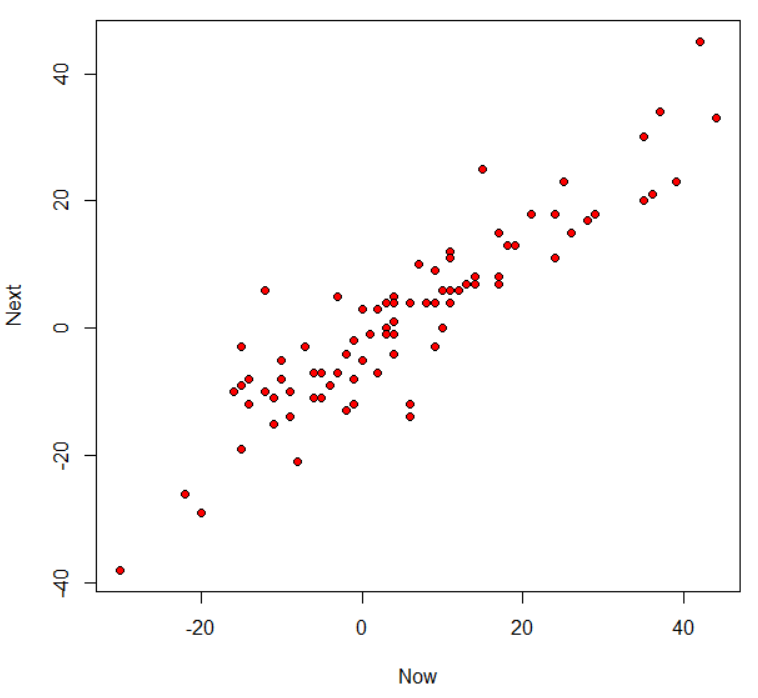
右肩上がりの散布図です。現状(Now)と先行き(Next)には正の相関があることがわかります。cor.test関数で相関係数を見てみます。

相関係数は0.9099091とかなり高い相関です。p-value < 2.2e-16です。95%信頼区間の相関係数は0.8640785から0.9407773となっています。現状(Now)と先行き(Next)には確固たる相関関係があります。
R言語で回帰分析をするには、lm関数を使います。
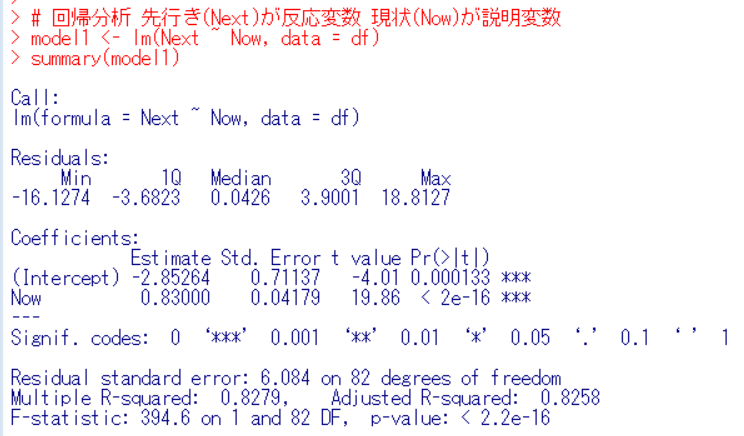
lm関数で回帰分析モデルを作ってsummary関数でモデルを表示します。
p-value < 2.2e-16と0.05以下ですから、この回帰分析モデルは有意です。
切片とNowの係数のp値はともに0.05以下ですので、どちらも意味があります。
Adjusted R-squaredが0.8258です。これはこのモデルが先行き(Next)の値の82.58%を説明できている、ということです。
この回帰分析モデル式は、
先行き(Next) = -2.85264 + 0.83000 * 現状(Now)
という式です。現状(Now)の値に0.83を掛けて、2.85264を引いた値が先行き(Next)です。
ここからは、Rクックブック Paul Teetor著を参考にしていろいろやってみます。
plot関数でこのモデルの残差プロットを見てみます。

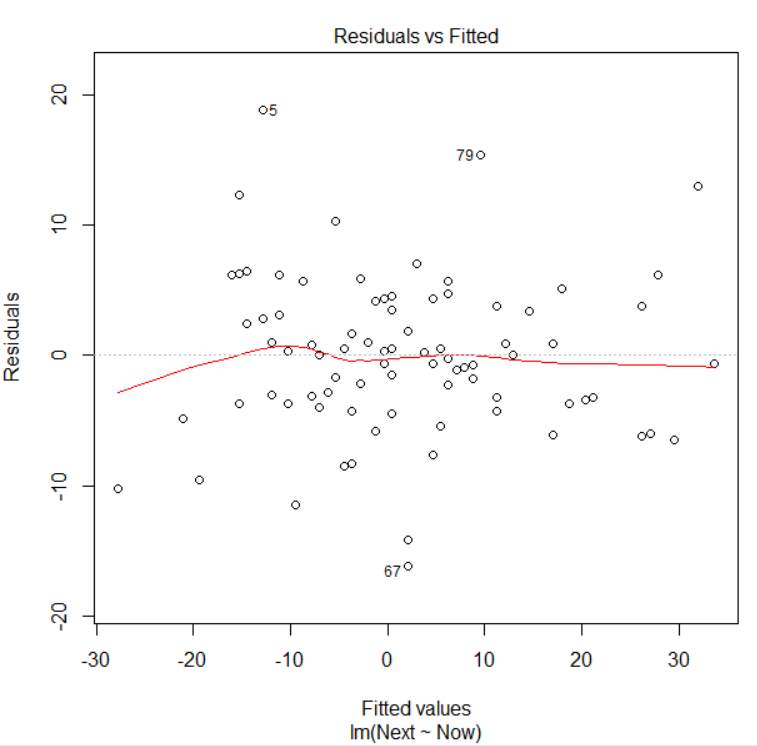
特に問題がありそうな残差プロットではないです。
confint関数で回帰式の係数の信頼区間がわかります。

Nowから一番低いNextを導出する式は、
Next = -4.2677804 + 0.746879 * Now
です。
その反対に、Nowから一番高いNextを導出する式は、
Next = -1.437496 + 0.931127 * Now
です。この二つの式の直線とmodel1の直線を散布図に重ね合わせてみましょう。

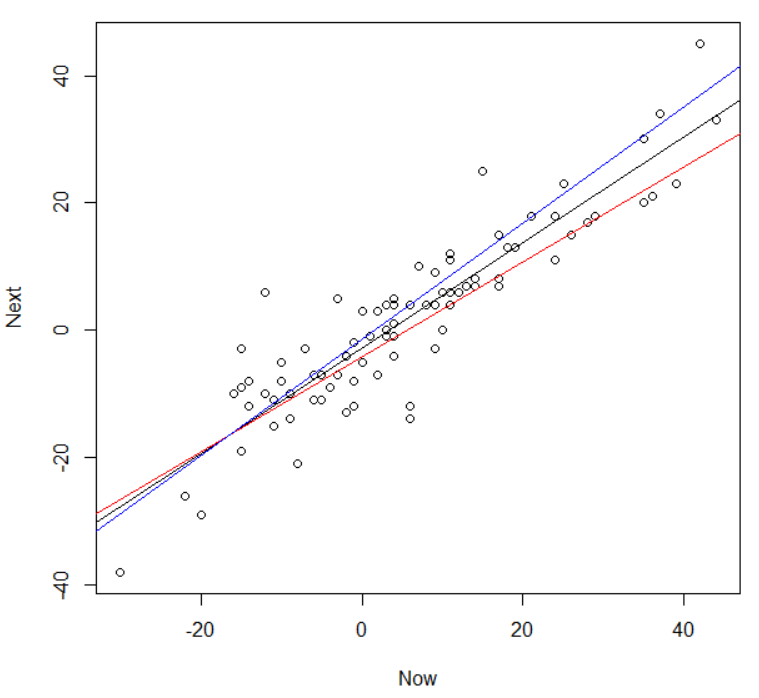
confint関数はmatrixオブジェクトになっていますので、confint(model1)[ , 1]で一列目の値を指定できます。
influence.measures関数で回帰分析モデルに大きな影響を与えている観測値がわかります。
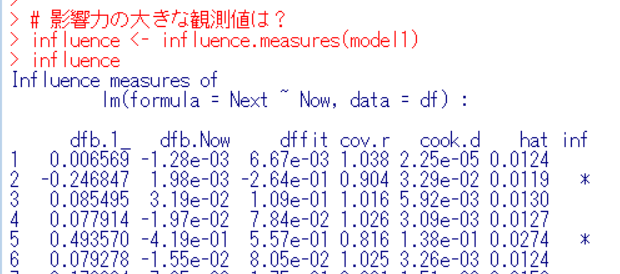
一番右のアスタリスクが大きな影響を与えている、という印です。このデータの番号を一つ一つ確認すればいいのですが、もっと効率的にやります。
まず。このinfluenceというオブジェクトには、$is.infで影響力があればTRUE、なければFALSEのマトリックスがあります。

このinfmtxというマトリックスを行で合計します。全部FALSEだったら0になってその行の観測値は影響が小さい、ということで一つでもTRUEがあれば1以上の値になってその観測値は影響が大きいとわかります。rowSums関数でマトリックスの行を合計できます。
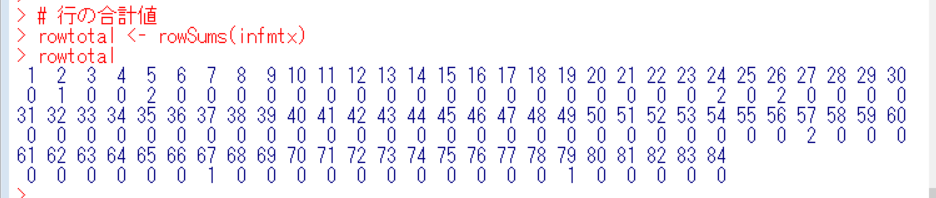
as.logical関数でTRUE/FALSEのベクトルに変換します。

このidxでデータフレームからTRUEの行だけ表示すればいいですね。
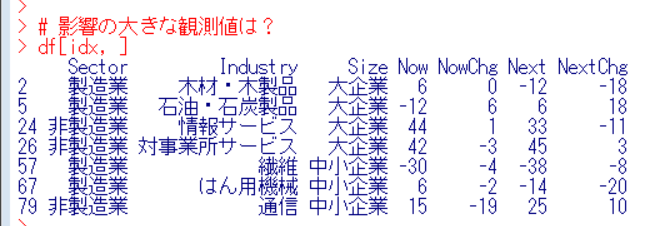
上の7つが回帰モデルに大きな影響を与えています。
散布図にしてみましょう。

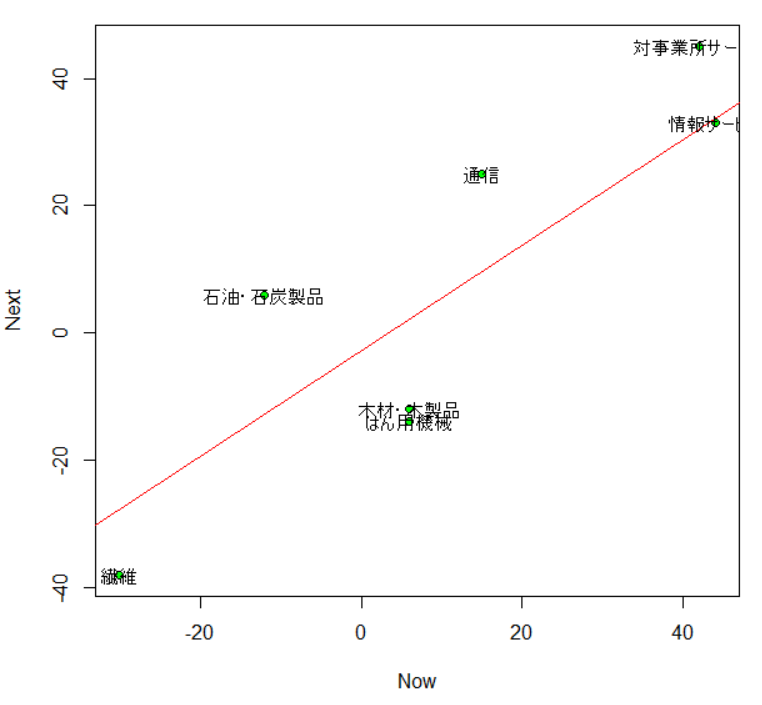
今回は以上です。
