の続きです。
今回は、企業の規模、大企業、中堅企業、中小企業の3つの企業規模で短観の値に違いがあるのかどうか、ANOVA(ANalyis Of VAriance)をしてみます。
まずは、現状(Now)のそれぞれの平均値を見てみましょう。tapply関数とmean関数を使います。

大企業の平均は9.92, 中堅企業の平均は9.61, 中小企業の平均は-0.14と中小企業は著しく低いですね。plot関数で箱ひげ図を描きます。

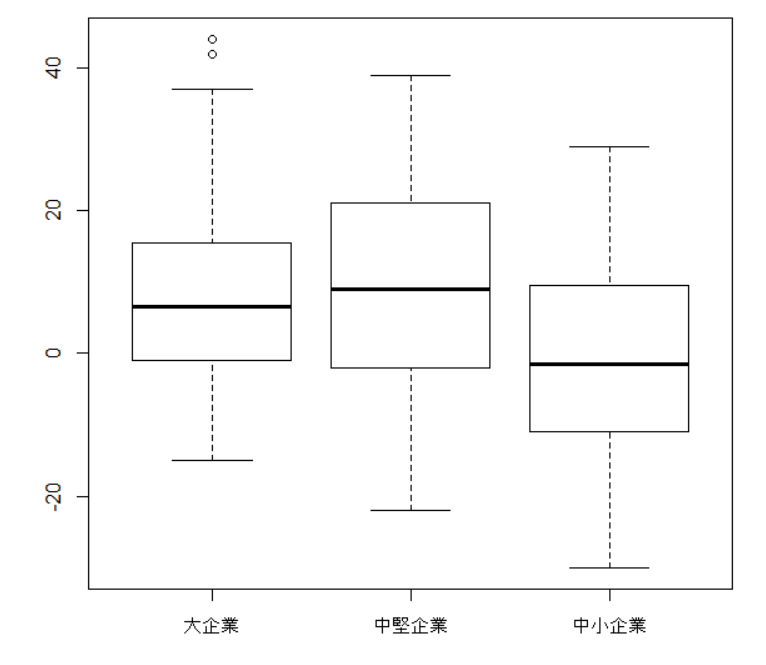
箱ひげ図を見ると、大企業も中堅企業も中小企業もけっこう上下の幅が大きいですね。平均値だけ見ると、絶対に中堅企業と中小企業では違いがあるな、と感じましたが、箱ひげ図を見た印象はそんなに違わないんじゃないか、と感じました。
実際はどうなんでしょうか?aov関数でANOVAができるそうです。やってみます。

p-value が0.0373と0.05よりも小さいので、Sizeの違いはNowの違いに影響していますね。
R言語では、aov関数で簡単にANOVAができますが、これを手作業(といっても計算はRでやります)でやったらどうなるでしょうか?練習と思ってやってみます。
Michael J. CrawleyのStatistics An Introduction using Rを参考にしてやってみます。

Statistics: An Introduction Using R (English Edition)
- 作者:Michael J. Crawley
- 出版社/メーカー: Wiley
- 発売日: 2014/09/23
- メディア: Kindle版
まずは、SSYというのを計算します。これは、個々の観測値から全体の平均値を引いて、それを2乗して、合計したものです。

SSYは21200.81となりました。この値は、aovのsummary画面のどこにあるかというと、

Sum Sqの1654と19547の合計値です。
次に、SSEを計算します。SSEはthe error of sum of squaresです。大企業、中堅企業、中小企業それぞれで、SSYのような計算をして、合計します。

このSSEの値、19546.791はaovの結果の

ここですね、Residualsの行のSum Sqの値が、SSEです。
そして、Sizeの行のSum Sqの値、1654がSSA(the treatment sum of suqares)です。
SSY = SSA + SSEという関係式が成り立ちます。
全体のバラツキ = ファクタ内のバラツキ + 残りのバラツキ
という関係かな。なので、SSA = SSY - SSEです。

そして、このSSAの自由度(Df)は、2です。大企業、中堅企業、中小企業と3つのファクターがあるから1引いて2です。SSA(Sum Sq)の1654を自由度2で割った値が、Mean Sqの827.0になります。

SSE(Residuals)の自由度はいくつでしょうか?全体の観測値の数は84です。SSYの自由度は83で、SSAの自由度は2ですから、83-2=81になります。
SSYの自由度 = SSAの自由度 + SSEの自由度
という関係ですね。
なので、SSE(Residuals)のMean Sqは、
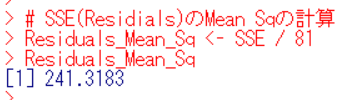
241.3183です。
aovの表でSSA(Size)のMean SqとSSE(Residuals)のMean Sqを確認しましょう。

そして、SSA(Size)のMean SqがSSA(Size)のvarianceで、SSE(Residuals)のMean SqがSSE(Residuals)のvarianceですね。この二つのvarianceの比を計算します。

この3.427がaovの結果画面のF valueの値です。
このF_ratioが統計的に有意かどうか、これをpf関数で計算します。

はい、この0.037263がaovの結果の一番右の列、Pr(>F)の値と一致しましたね。
これが手計算でのANOVAです。結構面倒ですね。これをaov関数で一瞬でできてしまうのがRの凄いところですね。
NowはSizeによって違いがあることがわかりました。Next(先行き)はどうでしょうか?

Next(先行き)も中小企業は低いですね。
箱ひげ図を描きます。

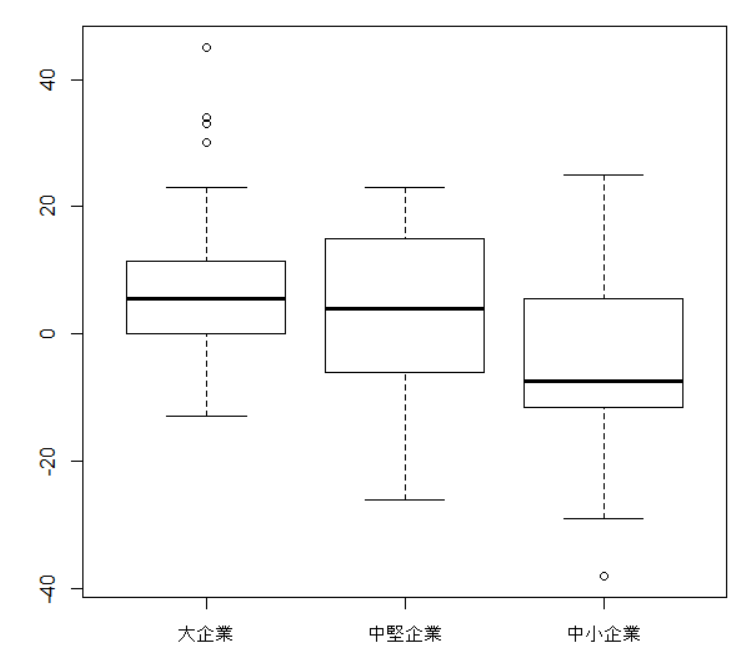
箱ひげ図はこんな感じでした。大企業のバラツキは小さいですね。
それでは、aov関数でANOVAを実行します。

p値は0.00727です。Nowのときよりも小さなp値ですね。Next(先行き)でも企業規模によって景況感は違うことがわかりました。
今回は以上です。