の続きです。
前回の分析で男性のほうが趣味・娯楽の平均時間が長い、無業者のほうが有業者よりも趣味娯楽の平均時間が長い、という傾向にあることがわかりました。
今回は、このことを統計検定してみましょう。2つの平均値に差があるかどうかという検定ですね。
まずは、男性のデータ、女性のデータをまとめたベクトルを作ります。

有業者と無業者合わせた男性の趣味・娯楽時間の平均値は、57.86分です。

女性のほうは平均時間は35.35分とやっぱり低いですね。
boxplot関数で箱ひげ図を描いて、MaleとFemaleを比較しましょう。
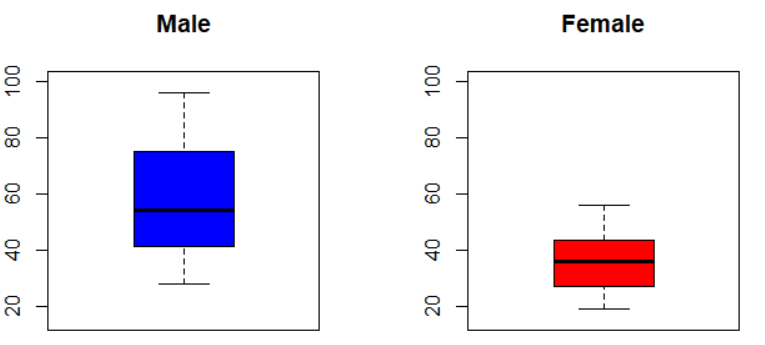
箱ひげ図を見ると、明らかに男性のほうが趣味・娯楽の時間が長いですね。
ここからは、
こちらの本、Statistics: An Introduction Using R の本を参考にして分析します。
まずは、分散の比較です。var.test関数を使います。

p値が2.2e-16と0.05よりも小さいので、MaleとFemaleでは分散は有意に違います。
分散が両者で違うので、Wilcoxon rank-sum testで両者の分布位置の違いを検定します。wilcox.test関数です。

p値は2.2e-16よりも小さいですから、MaleとFemaleは有意に分布の位置が違うということです。MaleとFemale, 男性と女性では有意に趣味・娯楽の時間が違います。
同じようにして、有業者と無業者でも比較してみます。

有業者の趣味・娯楽時間の平均値は34.01分、無業者のほうは59.21分ですから、無業者のほうが長いようです。
boxplot関数で分布を比べてみます。
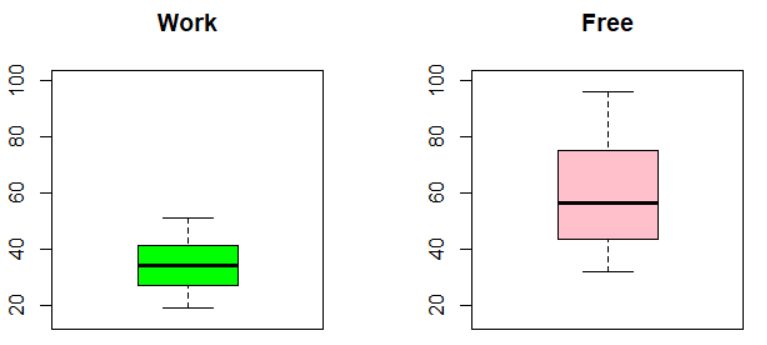
無業者のほうが長いですね。
var.test関数で分散、varianceを比較します。

p値が2.2e-16よりも小さいので、有業者と無業者の分散は有意に違います。
wilcox.test関数でWilcoxon rank-sum testを実行します。

p値が2.2e-16よりも小さいので、有業者と無業者の趣味娯楽時間の長さは有意に違うことがわかりました。
今回は以上です。
