の続きです。
今回は、lm関数で線形回帰と、randomForest関数でランダムフォレストを実行してみようと思います。
前回は、各変数の最小値や最大値を確認しました。
各変数の値の大きさがバラバラだとランダムフォレストに適さないので、まず各データ変数を最小値が0、最大値が1になるように標準化します。

apply関数とmin関数で各変数の最小値を取得します
apply関数とmax関数で各変数の最大値を取得します。
そうしたらscale関数で標準化します。
つぎの作業は、df3_scaledはデータフレームではなくてマトリックスなのでas.data.frame関数でマトリックスにします。

rownames関数で行名を都道府県にしました。
summary関数で確認すると、すべての変数が最小値が0で最大値が1になってることが確認できます。
boxplot関数で箱ひげ図を描いてみます。

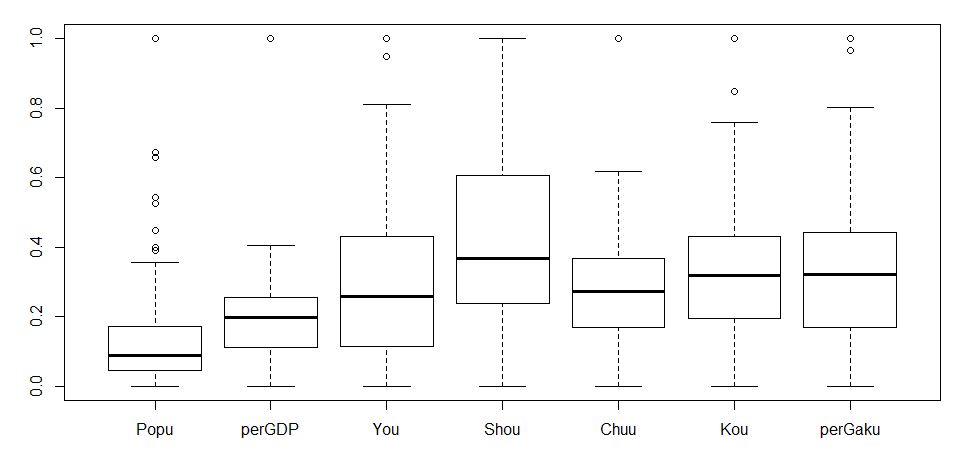
Popu(人口)が外れ値が多いですね。
plot関数で散布図マトリックスを描きます。

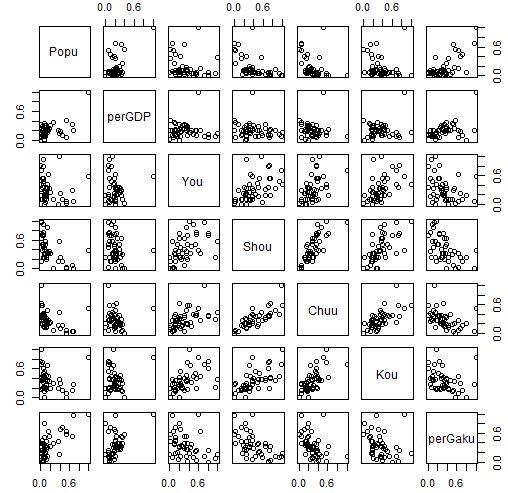
cor関数で相関係数マトリックスを出しましょう。

perGakuに一番相関しているのはPopuです。2番目がShouで、3番目がperGDPです。
それでは、perGakuを反応変数、その他を説明変数にして回帰分析をしてみます。
まずはlm関数で線形回帰分析をしてみます。

p-valueは3.076e-06ですから有意なモデルです。切片項とPopuだけが有意な変数ですね。Multiple R-squaredは0.5746ですから、このモデルで、perGakuが57.46%説明できます。
step関数でいらない変数を削除しましょう。

残った変数はPopuとShouだけでした。相関の高い2つの変数が残りました。
単純化していないモデル、LM1と単純化したモデルLM2のMSE(Mean Squared Error)を計算します。

単純化していないLM1のモデルのほうがMSEは少し小さいですね。
それでは、ランダムフォレストでperGakuを予測してみましょう。
はじめにrandonForestパッケージを読み込みます。

つぎは、randomForest関数でランダムフォレストモデルを作ります。
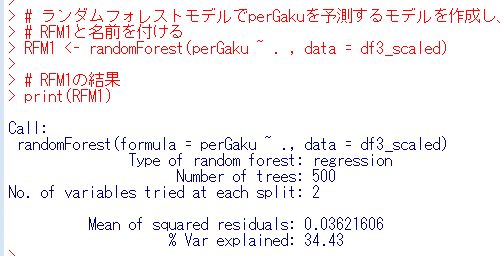
MSEが計算されました。0.036なので、lm関数のモデルよりも悪いですね。
さきほどと同じ手順でMSEを計算してみます。

同じ値になりました。
最後に横軸を実際のperGaku, 縦軸をそれぞれのモデルが予測した値の散布図を描いて、三つのモデルを比較してみます。

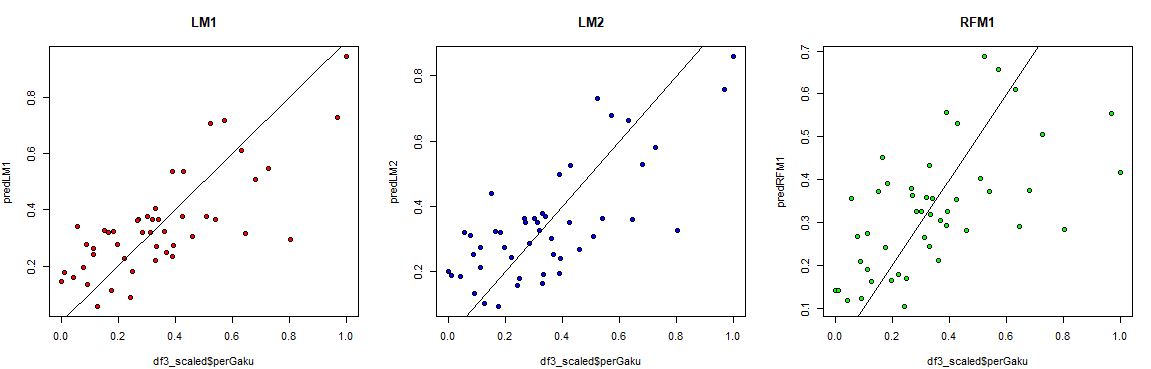
左が単純化しない線形回帰モデルのLM1
真ん中が単純化した線形回帰モデルのLM2
右がランダムフォレストモデルのRFM1です。
MSEが小さいモデルの散布図ほど、perGaku = 予測値 の直線の近くにプロットがあることがわかります。
今回は以上です。