の続きです。
今回は、学歴人口の比率、つまり分子は各学歴人口、分母は学歴人口合計を計算します。

最終学歴が小学校・中学校は計算しません。高校、短大・高専、大学・大学院の比率の合計の残りが小学校・中学校ですからね。
この3つの比率の分布形状をグラフで確認します。
最終学歴が高校の比率の分布形状です。

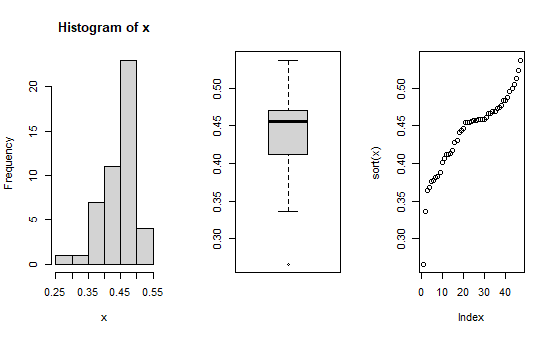
下方に一つ外れ値があります。
短大・高専の比率はどうでしょうか?

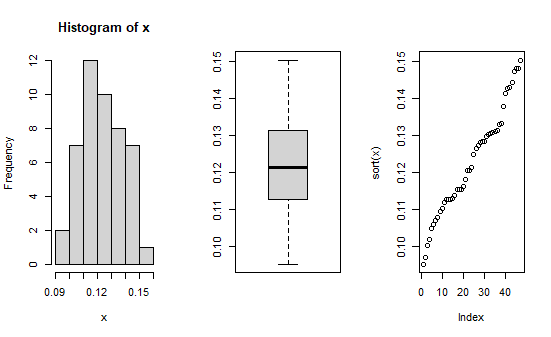
これは外れ値は無いようです。
大学・大学院の比率はどうでしょうか?

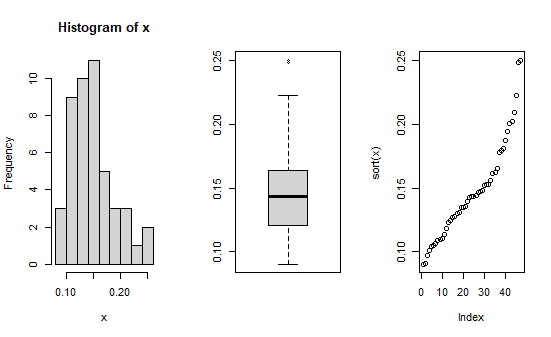
これは上に外れ値がありますね。
この3つの平均値や中央値、標準偏差、変動係数を計算しましょう。
準備として、平均値、中央値、標準偏差、変動係数を一度に計算する関数を作ります。

keisanという名前で関数を作りました。
それでは、最終学歴が高校の比率の平均値などを見てみましょう。

平均値は0.44, 中央値は0.46, 標準偏差は0.052, 変動係数は0.12です。
最終学歴が短大・高専の比率はどうでしょうか?

平均値は0.12, 中央値は0.12, 標準偏差は0.015, 変動係数は0.12です。
最終学歴が大学・大学院の比率の統計値はどうでしょうか?

平均値は0.15, 中央値は0.14, 標準偏差は0.039, 変動係数は0.26です。
3つの比率の中では、最終学歴が高校が一番平均値が大きく、変動係数は大学・大学院の比率が一番大きいことがわかりました。
今回は以上です。