の続きです。
今回はR言語でヒストグラムや散布図を描いてみます。
まずは、nobe: 1住宅当たり延べ面積(m2)のヒストグラムです。
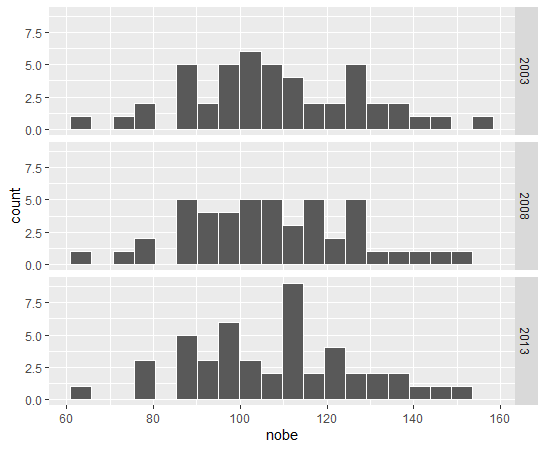
facet_grid()をつかって年度ごとにヒストグラムを描きました。年度による違いはあまりないようですね。
次は、mitudo: 人口密度(1ha当たり人口)です。

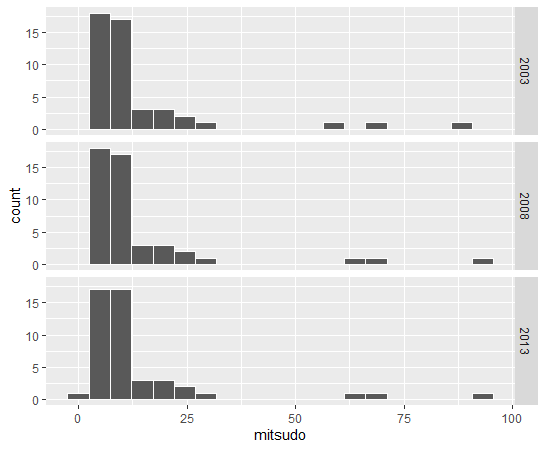
人口密度も年度による違いはなさそうです。値の大きいところが3つあります。
次は、per_capita17: 1人当り県内総生産額(平成17年基準、百万円)です。

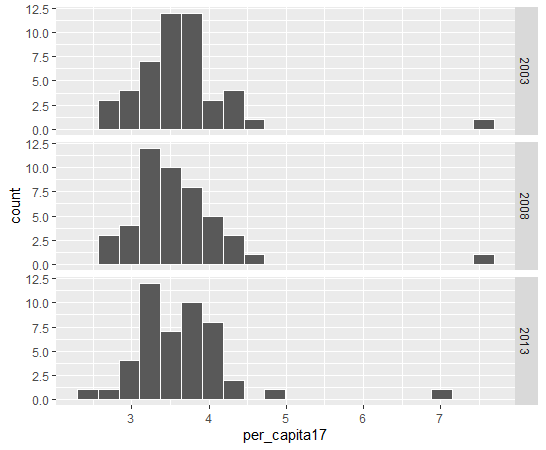
値の大きなところが一つあります。年度による違いはあまりないです。
per_setai: 1世帯当たり人数のヒストグラムはどうでしょうか?
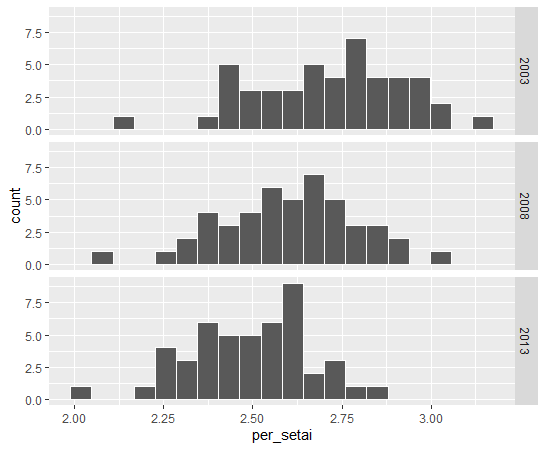
1人当たりの世帯人数は年をへるごとに減少しているように見えます。
年によって1世帯当たり人数に違いがあるかどうか、ANOVA分析で確認しましょう。
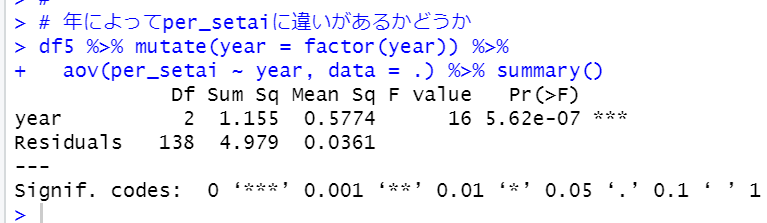
p値は5.62e-07と0.05よりも小さいです。やはり年によってper_setaiは値が違います。
都道府県別のグラフも描いてみます。まずはnobeから

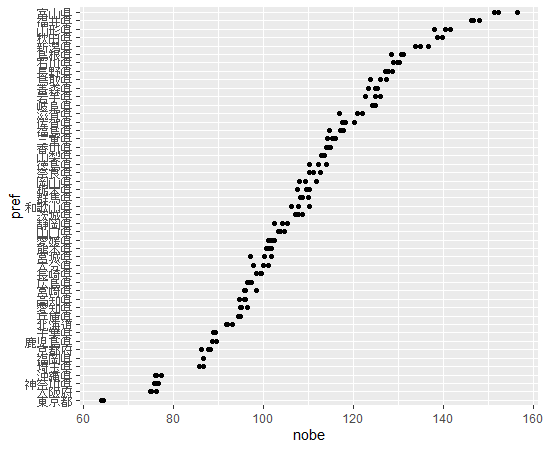
富山県、福井県、山形県などが面積が広く、東京都、大阪府、神奈川県などがせまいです。
mitsudoはどうでしょうか?

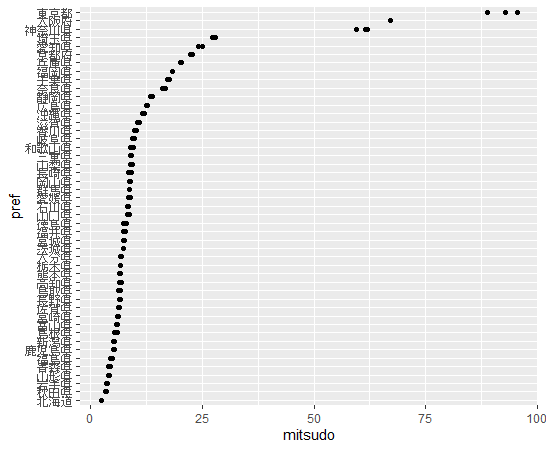
東京都がダントツで、神奈川県、埼玉県と続きます。北海道、秋田県、岩手県が人口密度が低いです。
per_capita17をみてみましょう。

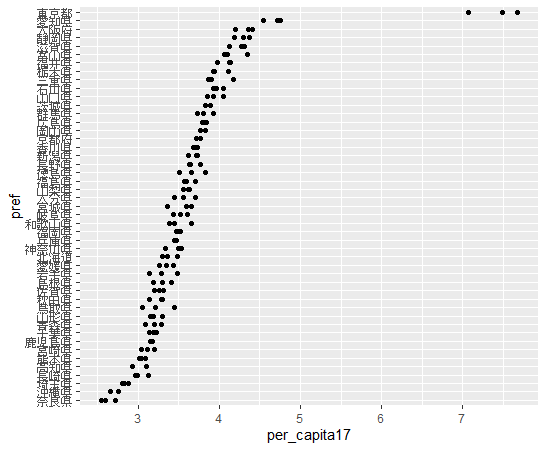
東京都がこちらも飛びぬけています。愛知県、大阪府と続きます。
奈良県、沖縄県、埼玉県が少ないです。
per_setaiはどうでしょうか?

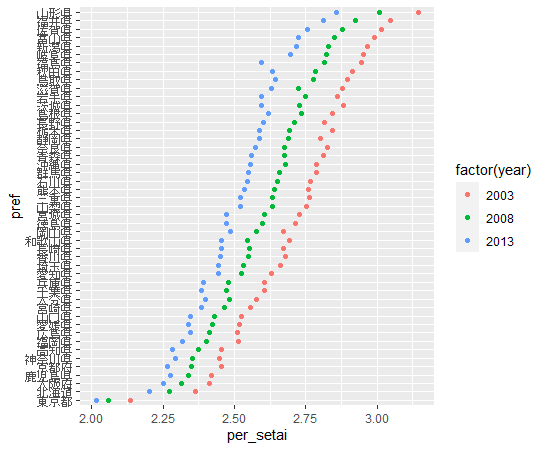
per_setaiは調査年度ではっきりと違いがありましたから、色分けしてみました。
山形県、福井県、佐賀県が人数が多く、東京都、北海道、大阪府が人数が少ないです。
続いて、各変数間の相関関係を調べてみましょう。nobeと相関が一番強いのはどこでしょうか?
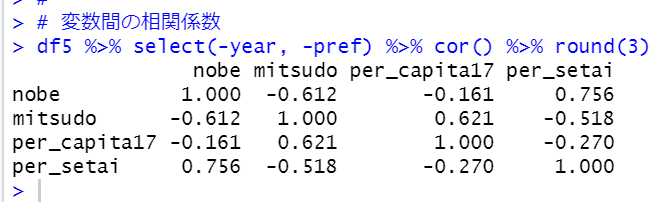
nobeと一番相関の強いのはper_setaiです。1世帯当たりの人数が多ければ家の面積も広い、というのは納得感があります。
以外なのは、per_capita17とnobeが-0.161とマイナス相関なことです。1人当たりの県内総生産額が増えれば広い家に住めると思うのですけどね。。
nobeとmitsudoの散布図を描いてみます。

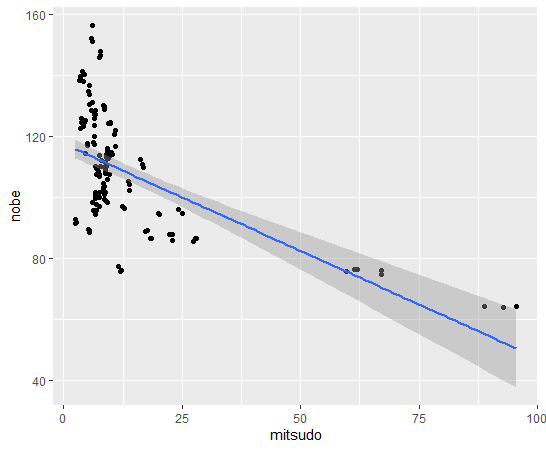
geom_smooth(method = "lm") を加えて、回帰直線を重ねました。
人口密度が高いほど、1住宅当たりの延べ面積は狭くなります。

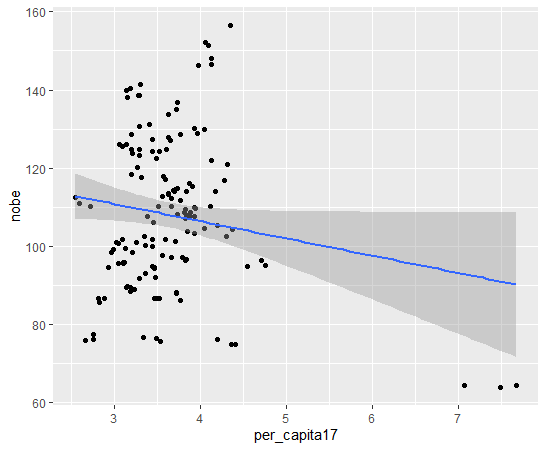
per_capita17ですが、右下の3つので点、東京都の影響でマイナスの相関になっているような気がします。東京都抜きで散布図を描いてみます。

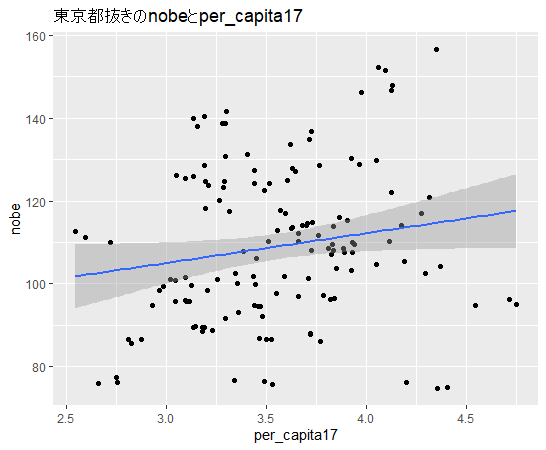
やっぱりそうですね。東京都抜きだと回帰直線の傾きが右肩上がりになりました。
回帰分析するときは東京都をダミー変数として加えたほうがいいかもですね。
nobeとper_setaiの散布図を見ましょう。

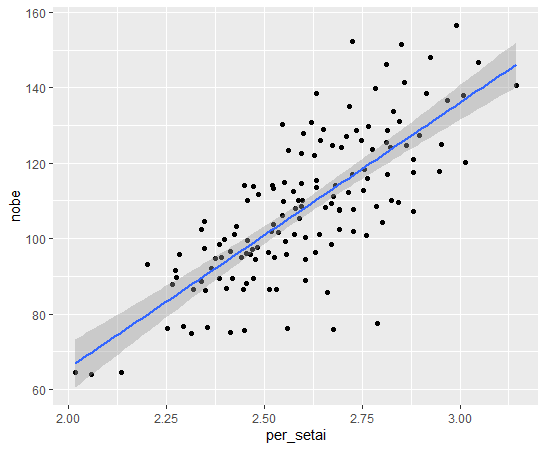
per_setaiの値が大きいほど、nobeの値が大きいというのがはっきりわかります。
今回は以上です。
次回は
です。
はじめから読むには、
です。