の続きです。
今回はnobe: 1住宅当たりの延べ面積(m2)を他の変数で回帰分析します。
前回の分析で東京都が特殊な感じだったので、東京都なら1、そうでないなら0のダミー変数を作っておきました。

lm関数で回帰分析モデルを作ります。

summary関数でモデルを表示します。
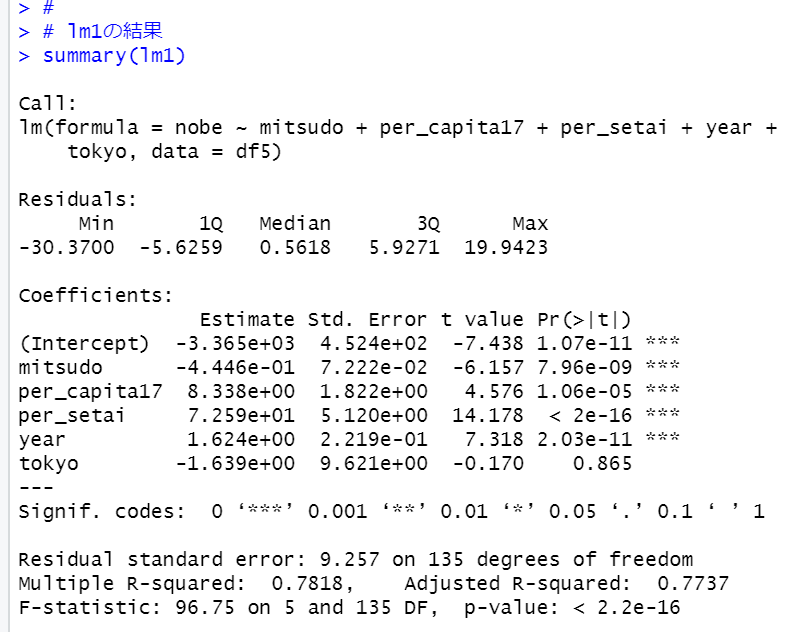
p-valueは2.2e-16よりも小さいので有意なモデルです。R-squaredは0.7818とかなり大きな値です。tokyoのp値は0.865なので必要なさそうですね。
tokyoの入らないモデルを作成します。

summary関数で結果を表示してみます。
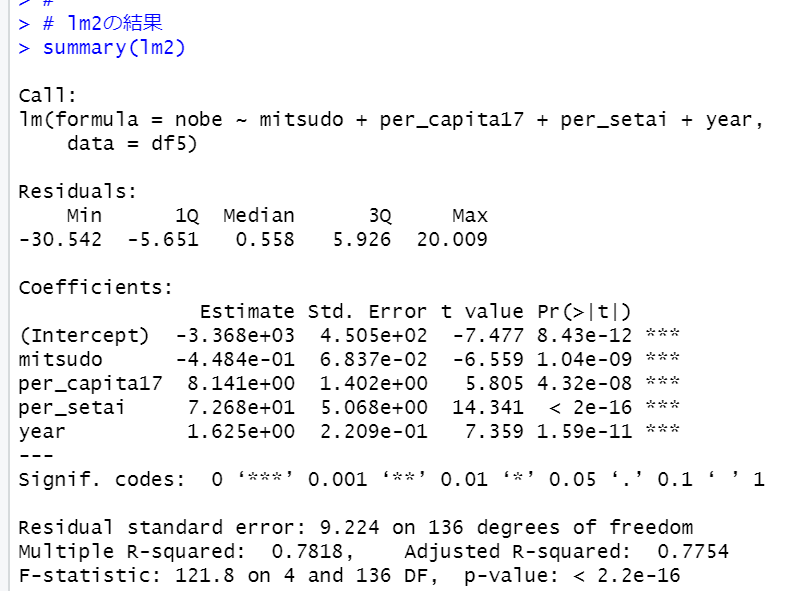
lm1とlm2に有意な違いがあるかどうか、anova関数で確認します。

p値が0.865ですので、lm1とlm2に有意な違いはありません。単純なlm2を採用します。
lm2をもう少しきれいな形式で出力します。broomパッケージを読み込んでtidy関数で出力します。

tidy関数で出力します。
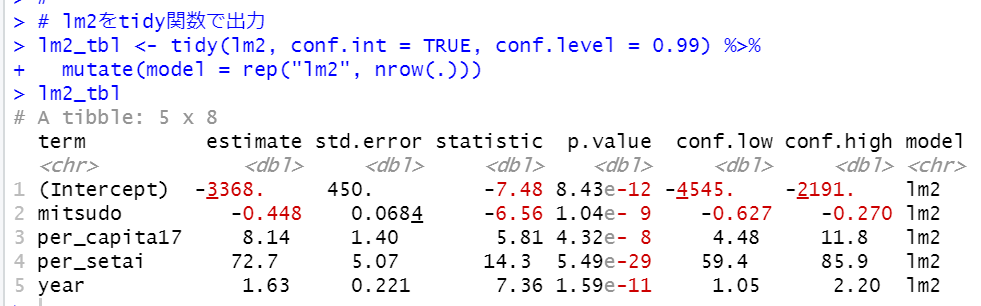
nobe = -3368 - 0.448 * mitsudo + 8.14 * per_capita17 + 72.7 * setai + 1.63 * year + u
というモデル式です。uは誤差項です。
per_capita17の係数がプラスになっています。
単純な相関係数ではnobeとper_capita17はマイナスの相関でしたが、mitsudo, per_setai, yearを固定すると、per_capitaが1、つまり1人当たりの県内総生産額が百万円増えると、8.14(m2)ほど延べ面積が広くなるということですね。
今回は以上です。
次回は
です。
はじめから読むには、
です。