の続きです。
前回はper_shobun: 食品営業施設当たりの処分件数をshishutsu: 消費支出で回帰分析しました。
今回はさらに変数を加えて回帰分析をしたいと思います。
はじめに、都道府県ごとの平均値のデータフレームを作りました。

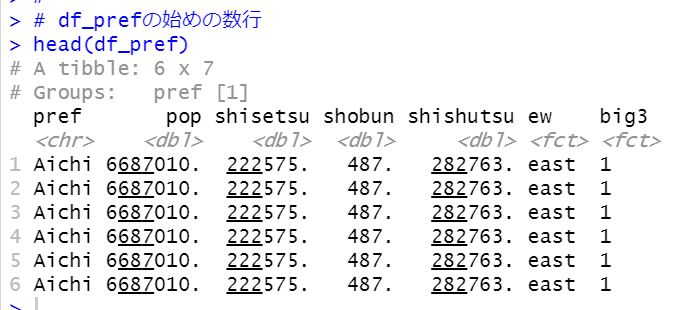
このように、同じ値の行が重複していますので、distinct関数で重複している行を削除します。

もう一度、head関数ではじめの数行を表示します。
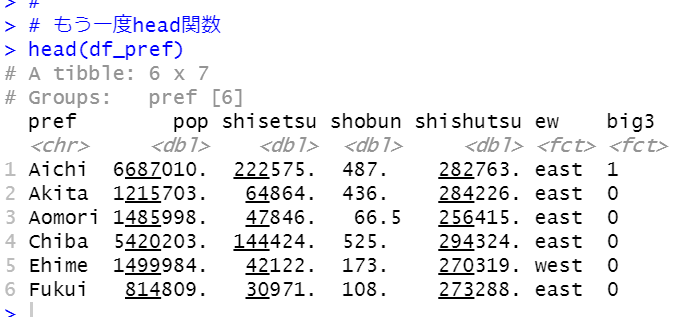
都道府県の重複がなくなりましたね。
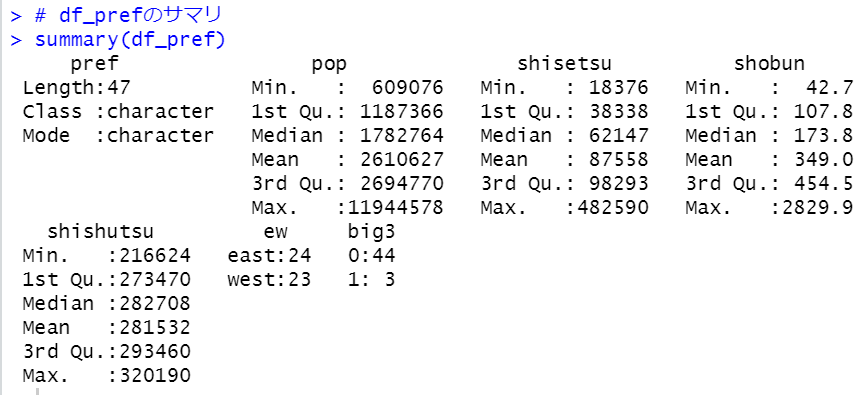
summary関数でデータフレームの概要をみます。
per_shobunを作ります。
今回は100万施設当たりの処分件数にします。
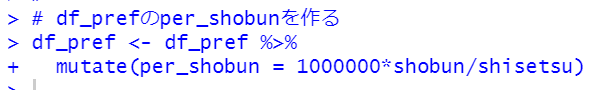
per_shobunの箱ひげ図をみてみます。
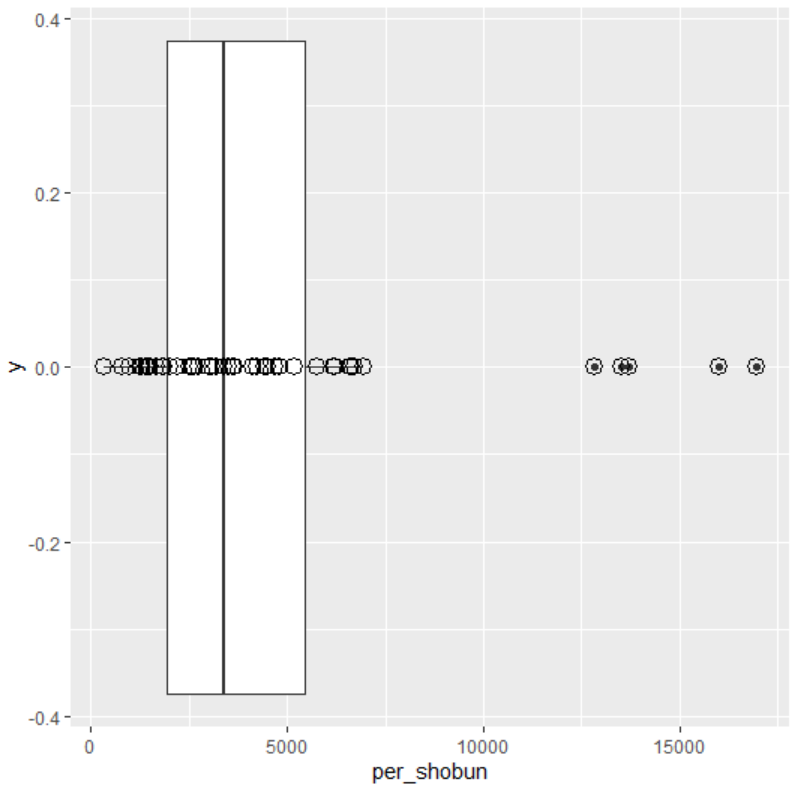
上方に外れ値があります。
散布図マトリックスをみてみましょう。

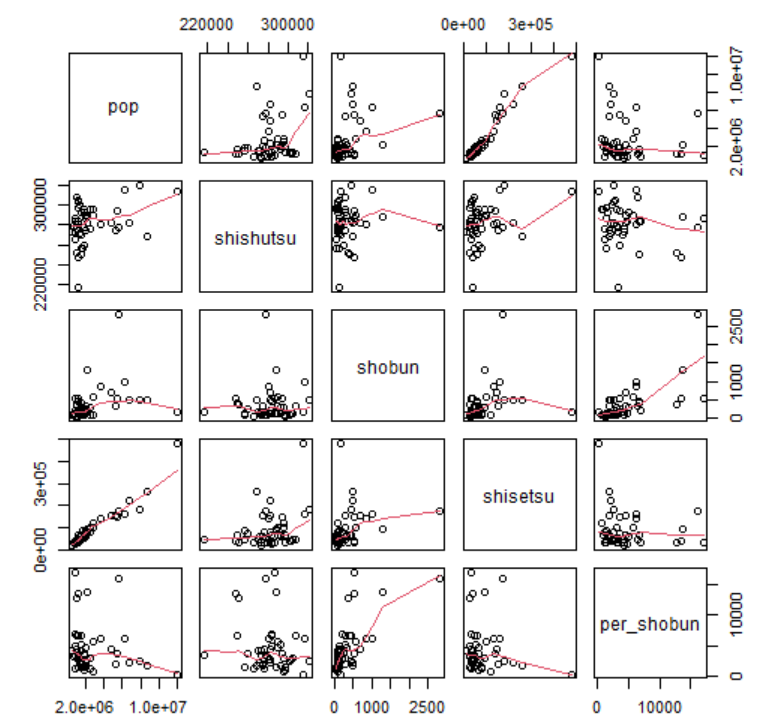
相関係数マトリックスをみてみます。

pop: 総人口とshisetsu: 食品営業施設数が0.962とかなり高い相関です。
per_shobunをpop, shishutsu, ew, big3の4つの変数で重回帰分析してみます。

回帰分析の式を 被説明変数 ~ (説明変数1 + 説明変数2 + 説明変数3)^2とすると、それぞれの説明変数の交差項も自動で作ってくれます。
p-valueが0.5052ということなので、有意なモデルでは無いです。
step関数でいらない変数・交差項を削除します。
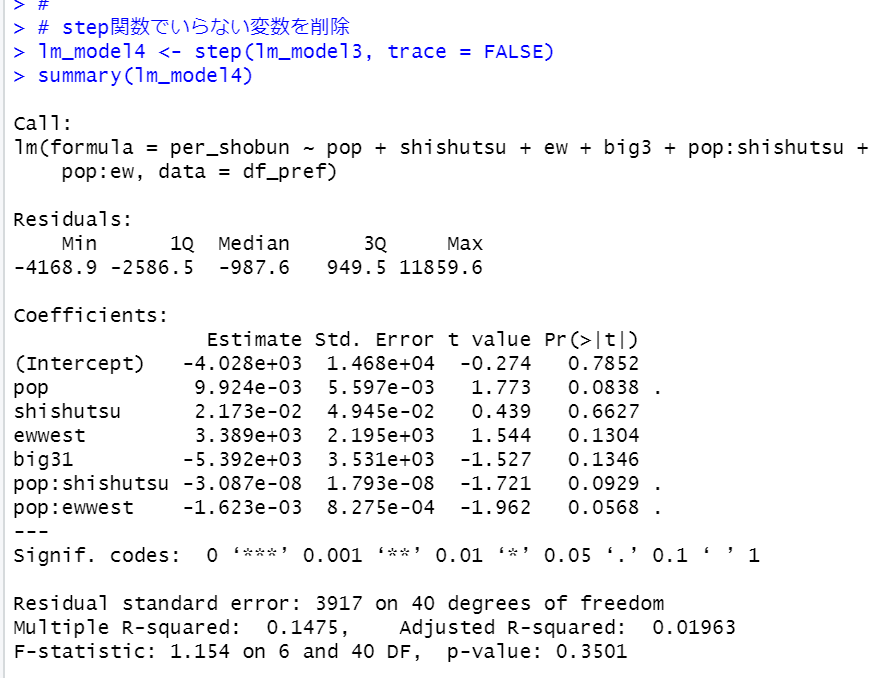
p-valueが0.3501なので有意な統計モデルでは無いですね。big3のp値が0.1346と0.05より高いので削除してみます。
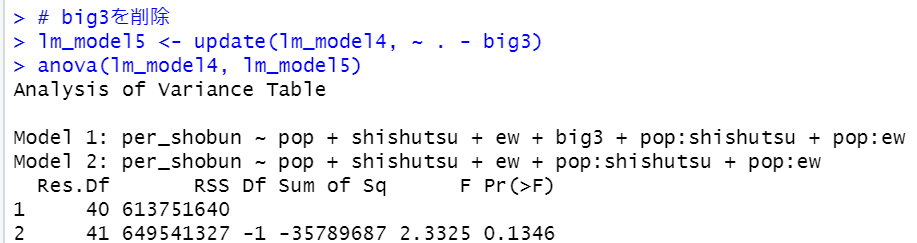
update関数でbig3を削除して、anova関数で削除前のlm_model4と削除後のlm_model5を比較しています。p値は0.1346なので有意な違いはありません。
summary関数でみてみます。

p-valueが0.4974なので有意なモデルではないですね。pop:shishutsuを削除してみます。

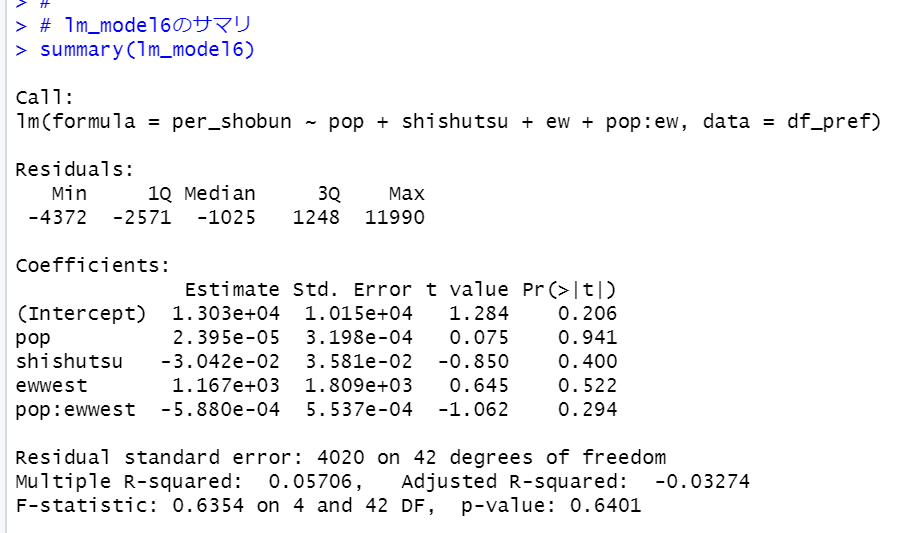
p-valueが0.6401なので有意なモデルではないです。どんどんp-valueが大きくなっていますね。。pop:ewも削除します。

p-valueは0.7048で有意なモデルではないです。ewを削除します。

p-valueが0.495ですので有意なモデルではないです。
popを削除します。

p-valueは0.3146と0.05よりも大きく有意ではないです。
shishutsuも削除します。つまり切片項だけのモデルです。
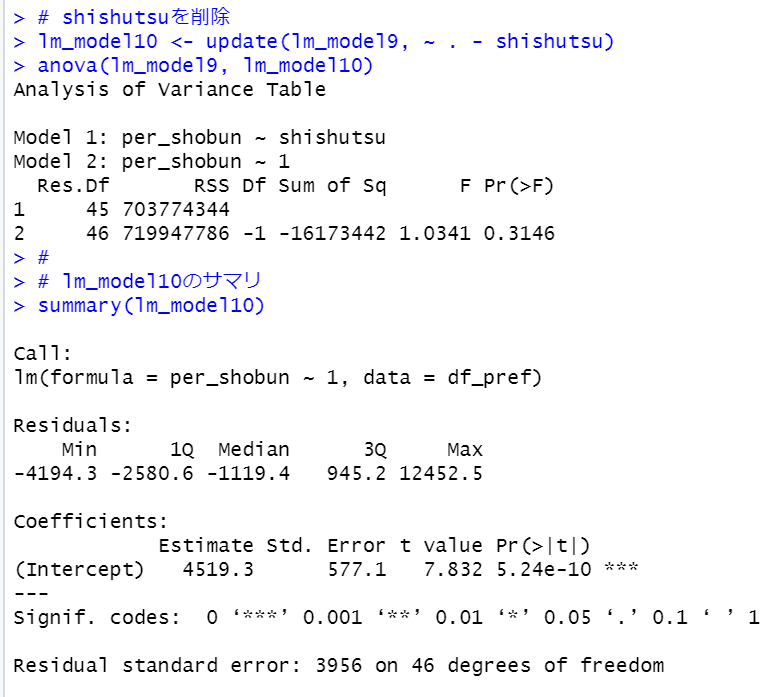
p値が5.24e-10と有意になりました。
つまり、per_shobunはpopやshishutsuとは関係なく、平均4519.3ということです。
95%の信頼区間を求めましょう。

別の方法でも求めてみます。

値が少し違うのは、per_shobun_avgが4519.309, sqrt(per_shobun_var/n)が577.0622とより細かい値だからですね。
今回は以上です。
はじめから読むには、
です。