
Photo by Tim Mossholder on Unsplash
の続きです。
今回はriyou以外の各変数の分布をみてみます。
まずは、mitsudo: 可住地面積1平方キロメートル当たりの人数、つまり人口密度です。

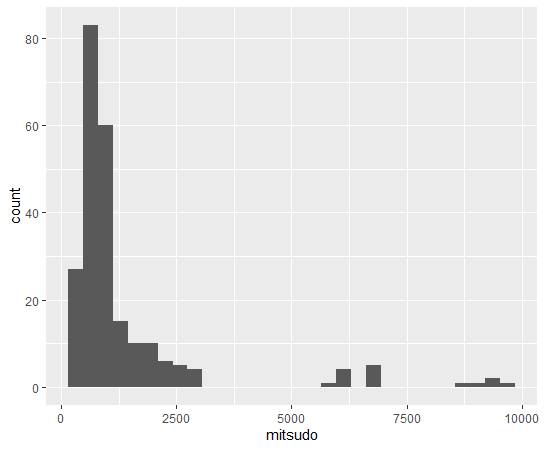
右のほうに外れ値っぽい分布があるのがわかります。
対数変換してヒストグラムを描いてみます。

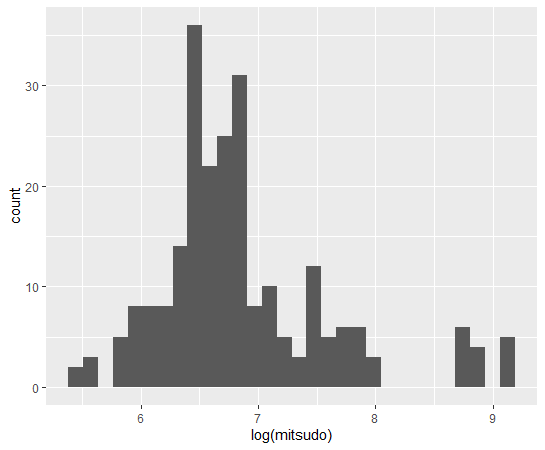
対数変換した値のほうが左右対称に近い分布になりますね。
データ分析するときは、左右対称の分布のほうが扱いやすいです。
skewという値を計算して分布の左右対称度合いを測ります。
まず、skewを計算する自作関数を作ります。

この自作関数でmitsudoとlog(mitsudo)のskewを計算します。

対数変換したmitsudoのほうが0に近いので左右対称に近いです。
対数変換したmitsudoをデータフレームに追加します。
続いて、shotoku: 1人当たり県民所得(千円)のヒストグラムを描いてみます。

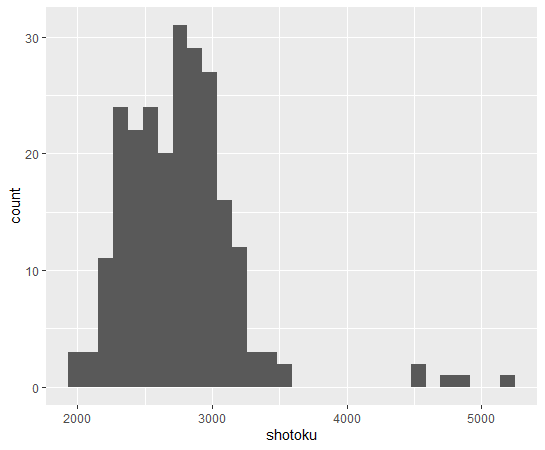
これも右のほうに外れ値のようなものがありますね。
対数変換したshotokuのヒストグラムを描いてみます。

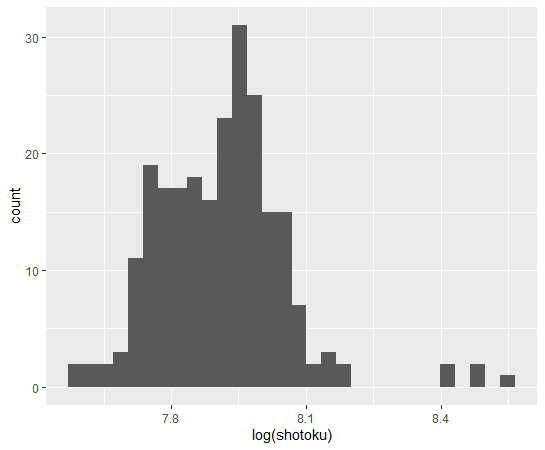
少しはましになったかな?
skewを計算してみます。

対数変換したshotokuのほうが0に近いので、より左右対称に近いということです。
対数変換したshotokuをデータフレームに追加します。

iryou: 1人当たり医療費(千円)のヒストグラムを描いてみます。

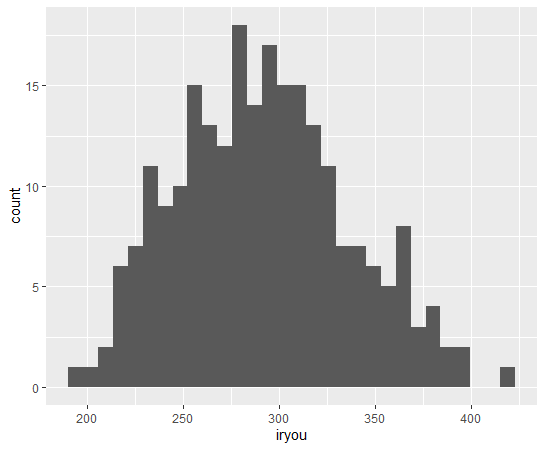
これは前の2つと比べると左右対称に近いですね。
対数変換したiryouのヒストグラムを描いてみます。

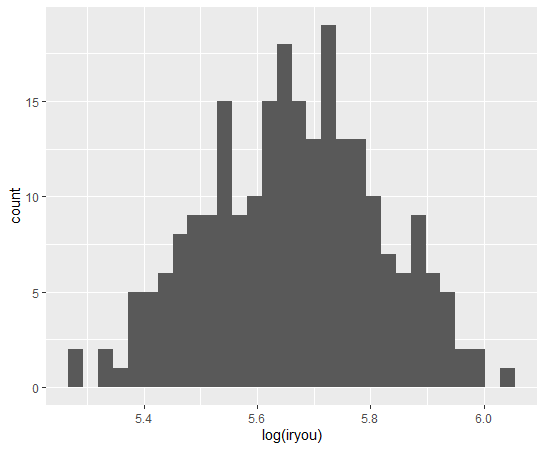
これも左右対称に近いですね。
見た目ではそのままのiryouと対数変換したiryouのどちらが左右対称に近いか判断できないです。skewを計算してみます。

対数変換したiryouのほうが0に近いです。
対数変換したiryouをデータフレームに追加します。

今回は以上です。
次回は
です。
はじめから読むには
です。