
Photo by shay cohen on Unsplash
の続きです。前回は都道府県別の平均値のデータフレームで回帰分析しましたが、今回は生のデータフレームで回帰分析してみます。
まず、変数間の散布図マトリックスをみてみます。

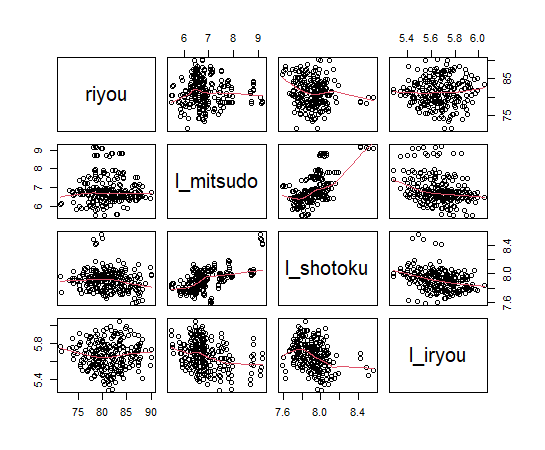
相関係数マトリックスもみてみます。

riyouとl_mitsudoの相関係数は-0.013, l_shotokuとの相関係数は-0.160, l_iryouとの相関係数は0.025です。一番相関係数(の絶対値)の大きな組み合わせは、l_mitsudoとl_shotoku で0.618です。
それではR言語のlm()関数で回帰分析してみます。

前回の回帰分析と違うのは、factor(year)を加えています。
年によってriyouは平均的な水準が違うのがわかります。
l_iryouの係数を見ると、12.1682です。
前回のreg2ではl_iryouの係数は11.8724でしたのであまりかわらないですね。
前回のreg2とreg3の各変数の係数や標準誤差などを比べてみます。
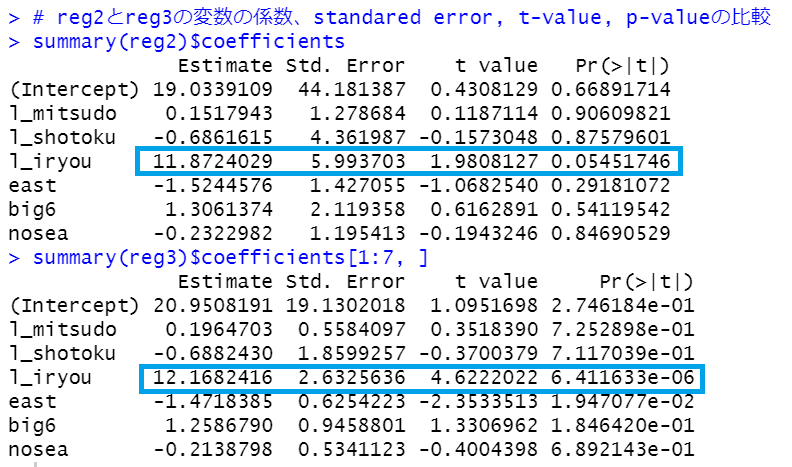
l_iryouのところを青く囲みましたが、dfで回帰分析した結果のほうが標準誤差が小さくなっていることがわかります。dfのほうが観測数が多いからですね。
残差プロットをみてみます。
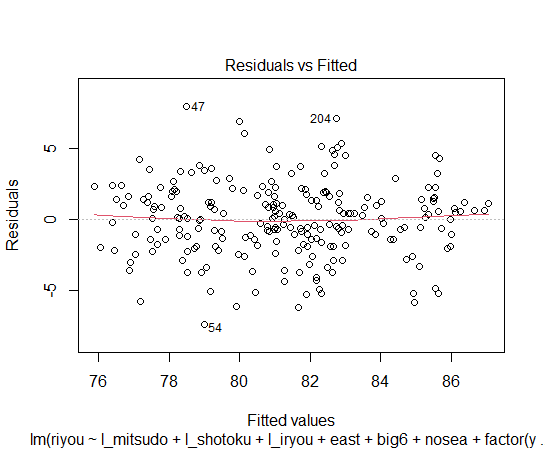
残差に不均一性は見られないようです。
念のため、Breusch-Pagan Testをしてみます。
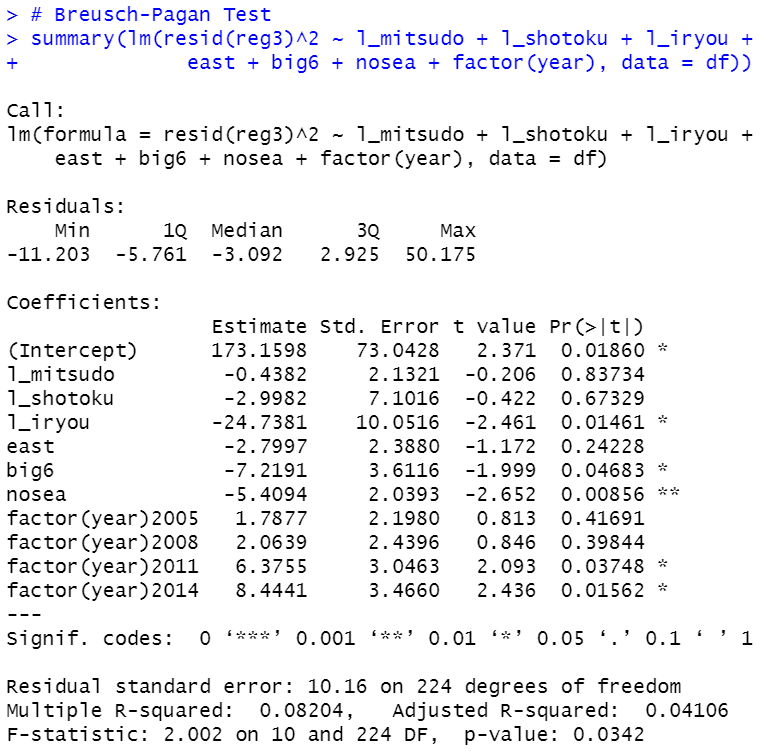
p-valueが0.0342と0.05よりも小さいので均一分散であるという帰無仮説を棄却します。
lmtestライブラリーとcarライブラリーを読み込んで、
heteroskedasticity robustな標準誤差をみてみましょう。
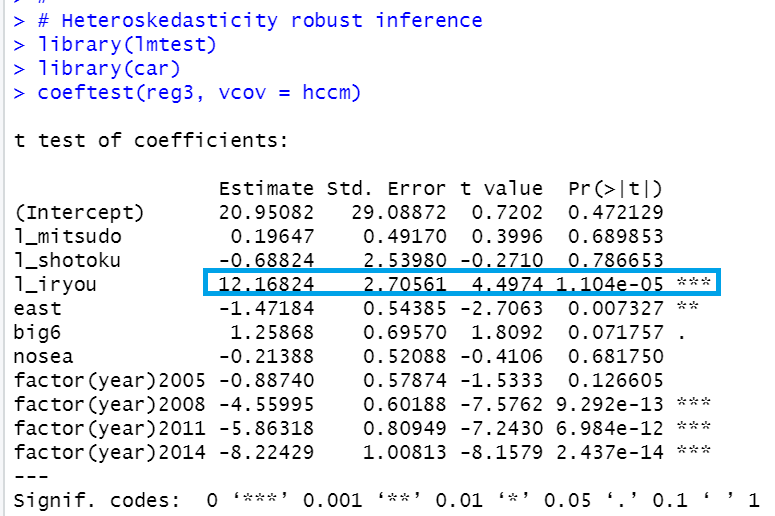
l_iryouの標準誤差は2.706と少し大きくなりましたが、0.1%水準で有意であることはかわらないです。
医療費(iryoy)が1%増えると病院病床利用率は0.12ポイント高いということですね。
今回は以上です。
はじめから読むには
です。