
Photo by Sana Ullah on Unsplash
の続きです。
通院者率は、oldr: 65歳以上の人口割合がと関係があるかどうかを調べてみます。
やっぱり歳をとってくると病院のお世話になることが若いときよりも多くなると思うんですよね。
oldrがある年を確認します。

2005年から2019年まで毎年、データがあるのですね。
一番古い年でoldrとhosp: 人口1000人当たりの通院者率のあるのは2007年、一番新しい年で両方にデータがあるのは2019年です。
この2007年と2019年のデータを使って、oldrとhospの散布図を描いてみます。

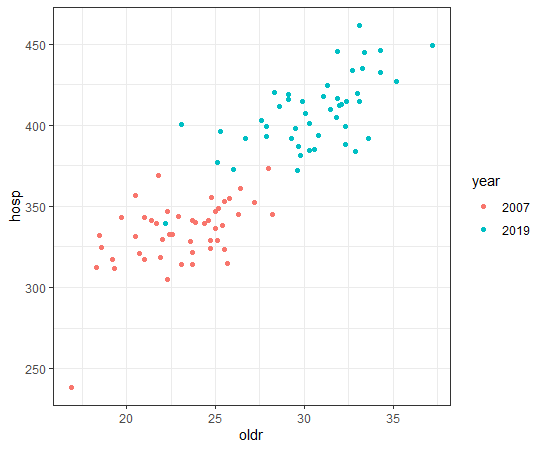
2007年と2019年で分布範囲は違っていますが、oldrとhospに正の相関関係があることは間違いないようですね。
lm()関数で回帰分析してみましょう。
2007年と2019年だけのデータフレームを作ります。

worr: 従業者率とgymn: 人口100万人当たりの社会体育施設数は2007年と2019年はデータが無かったのですね。
yearというファクタ型の変数で2007と2019を区別できるようにしておきました。
それでは、回帰分析をしてみます。

このモデル全体のp-valueは2.2e-16よりも小さいので有意な統計モデルです。
hosp = 156.4482 -+ 7.9904*oldr + u
という推定式です。uはerror termです。
つまり、oldrが1ポイント上昇すると、通院者率が約8人増えるということです。
残差プロットを描いてみます。

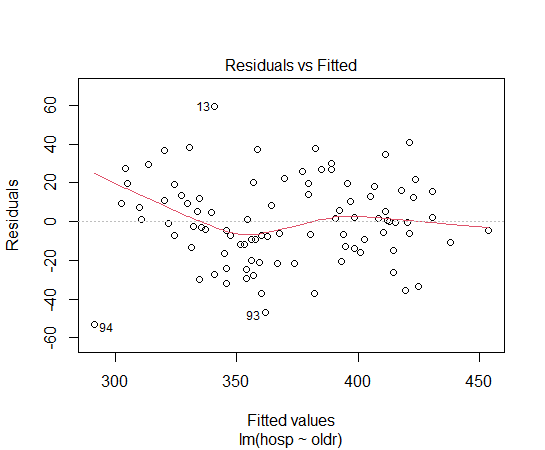
残差が適当に散らばってみえますので、heteroskedasticity(誤差項の不均一分散)ではないようです。
確認してみましょう。
にあるSpecial Case of the White Test for Heterosjedasticityの方法でやってみます。

p-value: 0.3069ということなので、uhat2 = yhat + yhat^2 + error という回帰式は有意ではないです。つまり、heteroskedasticity(誤差項の不均一分散)ではないということですね。
今回は以上です。
次回は
です。
はじめから読むには
です。
