
の続きです。
前回まではクロスセクションデータの分析でした。今回は時系列データの分析をしてみます。
まず、東京都だけのデータフレームを作成します。
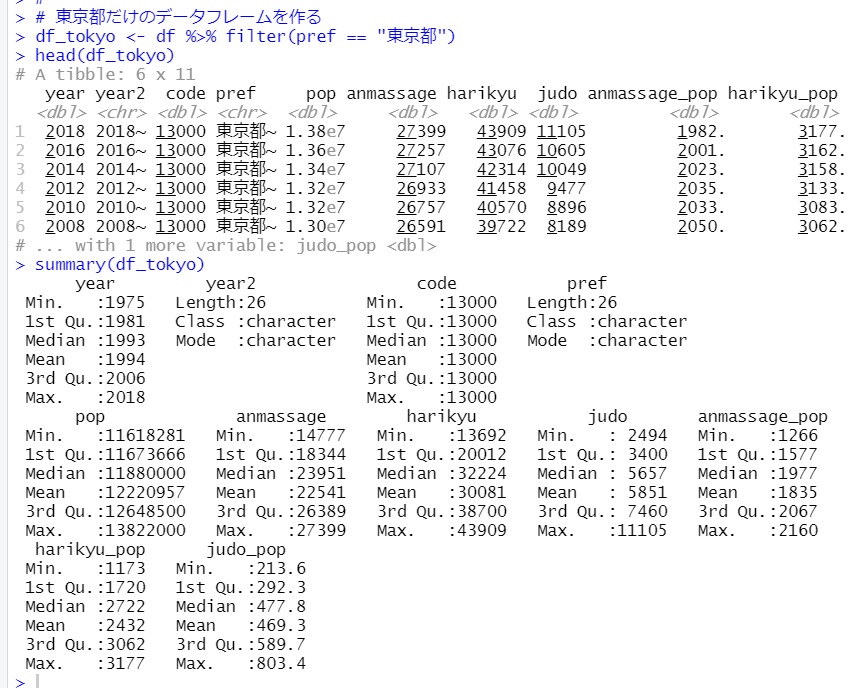
filter()関数で東京都だけにしました。このデータフレームをts()関数でtsオブジェクトにします。不必要なyear2, code, prefという変数は削除しましょう。

str()関数でオブジェクトの構造を見ると、Time-Seriesオブジェクトになっていることがわかります。
plot()関数で簡単に経年変化のグラフが描けます。

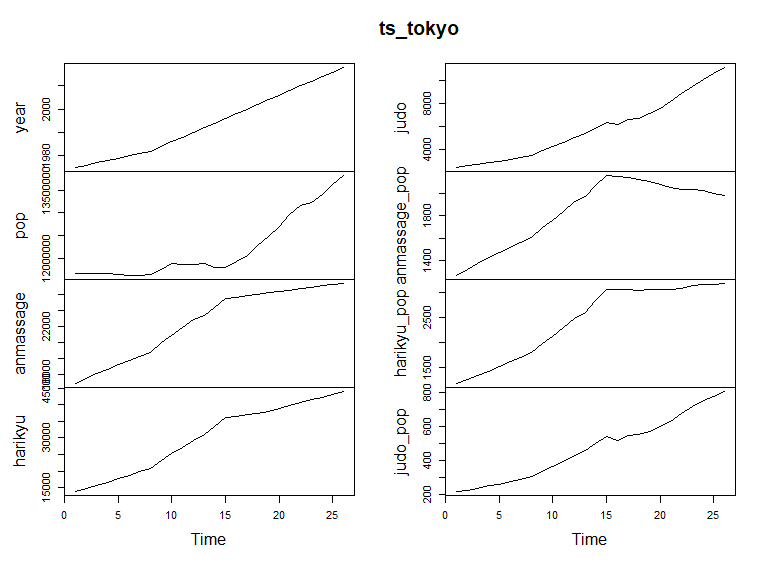
こうしてみると、柔道整復師の数は実際の数も人口当たりの数も順調に伸びていますが、あんま・マッサージ師の数は頭打ちのような感じで、人口当たりの数は減っていることがわかります。
anmassage_pop: 人口百万人当たりのあんま・マッサージ師の数を被説明変数にして、harikyu_pop: 人口百万人当たりのはり・きゅう師の数と
judo_pop: 人口百万人当たりの柔道整復師の数を説明変数にして回帰モデルを作成してみます。
lm()関数でできます。

harikyu_popの係数の符号は正で、judo_popの係数の符号は負です。どちらの係数も有意な係数のになっています。
時系列データを回帰分析するときに便利なパッケージがありまして、dynlmパッケージというのがあります。これを使うと、ラグ変数やトレンド変数、変数差分などを簡単に回帰モデルの中に追加できます。
まずは、dynlmパッケージを読み込んでみます。

3つの変数はどれも基本的に右肩上がりのトレンドでしたので、トレンド変数を追加して回帰分析してみましょう。

dynlm()関数で回帰分析モデルを作り、trend()でトレンド変数を追加できます。トレンド変数は統計的には有意ではないですね。
dynlm()関数では、L()でラグを追加できます。harikyu_pop, judo_popのラグを追加したモデルをみてみましょう。

L(harikyu_pop)の係数の符号はマイナスで、統計的に有意ですね。一つ前のharikyu_popの値が大きいほどanmassage_popの数は小さいということですね。
dynlm()関数ではd()というので差分を作ることができます。harikyu_pop, judo_popの差分を説明変数にして回帰分析モデルを作ってみましょう。

決定係数R2は他のモデルと比較してかなり小さいですが、それでもd(harikyu_pop), d(judo_pop)の係数は統計的に有意です。
ts()のトレンド、L()のラグ、d()の差分、この3つを全部入れた回帰分析モデルを作ってみましょう。

ラグについては、L(変数, 2)として2期前の値にしています。これは、L(変数)とd(変数)を同時に入れることはできないからです。
harikyu_popは正の符号で統計的に有意、judo_popは負の符号で統計的に有意ですね。
これは全部のモデルで共通しています。
stargazer()関数で差分のモデルを除いた4つのモデルを比較してみます。
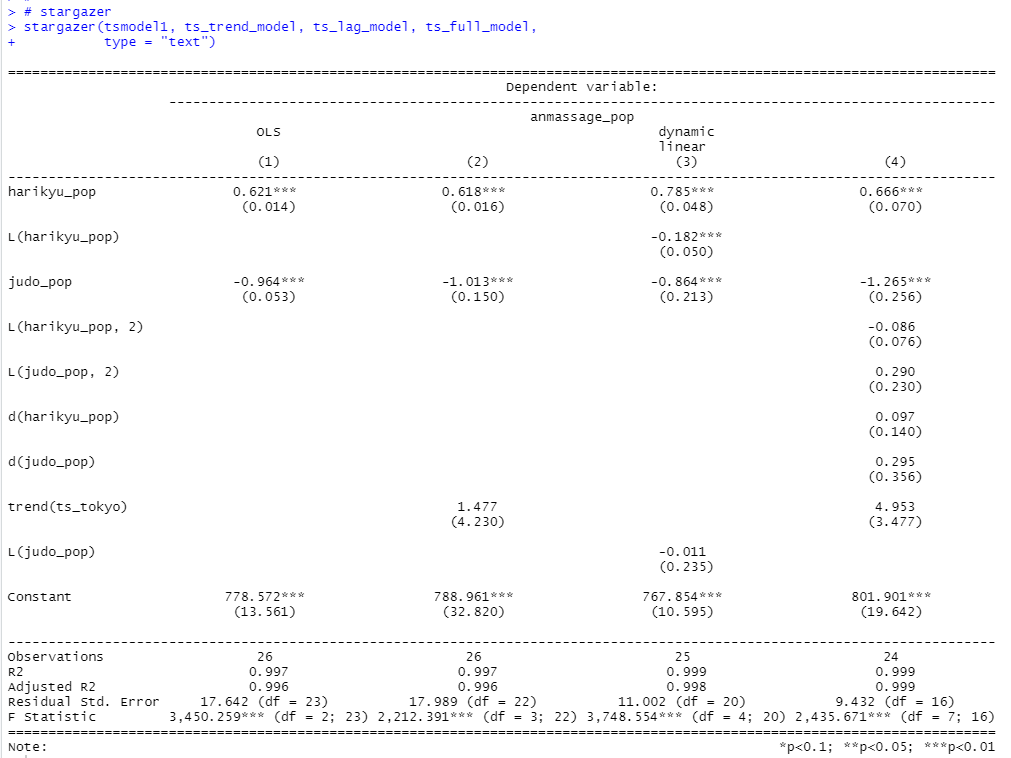
前回のクロスセクションデータの回帰分析では、はり・きゅう師の数が増えたらあんま・マッサージ師の数が増えていました。今回の時系列データの回帰分析でも同じようにはり・きゅう師の数が増えるとあんま・マッサージ師の数も増えていました。
今回は以上です。
次回は
です。
初めから読むには、
です。