
Photo by Marc Schulte on Unsplash
今回は、Sex、性別のデータを調べます。まずはtable()関数で度数を見ます。

femaleは女性で、466人です。maleは男性で843人です。
prop.table()関数で比率にしてみます。
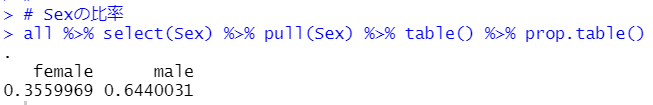
女性が36%、男性が64%という割合ですね。
trainのデータとtestのデータで分けて度数、比率を見てみます。

trainのデータは、女性が35%、男性が65%です。

testのデータは、女性が36%、男性が64%です。
だいたい同じような比率ですが、統計的に有意な違いがあるかどうかをprop.test()関数で確認します。
prop.test(c(trainの女性の数, testの女性の数), c(trainの数, testの数))という構文になります。

p-valueは0.7388と0.05よりもはるかに大きいので、trainとtestではSexの比率に統計学的に有意な違いはありません。
続いて、trainのデータで男性と女性の生存確率を見てみます。
まずは、Sexからfemaleだったら1、maleだったら0というダミー変数、femaleを作成します。

この作成したfemaleを説明変数にして、Survivedを被説明変数にしてlm()関数で回帰分析します。

Interceptの0.18891がmale(男性)の生存確率です。18.9%です。
女性の生存確率は、このInterceptの0.18891にfemaleの係数の0.55313を足して、
0.74204です。74.2%ということですね。
今回は以上です。
次回は、
です。
初めから読むには、
です。