
Photo by Edouard TAMBA on Unsplash
今回はAgeについて分析します。まずはsummary()関数でNAの有無や平均値などを確認します。
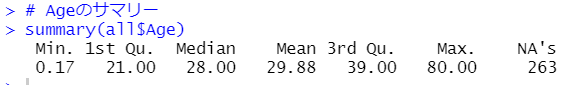
NAが263個もあります。最小値は0.17で最大値は80、平均値は29.88で中央値は28.00です。
NAがあるので、NAなら1、そうでないなら0というダミー変数と、NAなら0、そうでないならそのまま、という調整をした変数を作成します。

まずはna_ageについてtrainとtestで違いがあるかどうかを見てみます。

mean()関数で平均値を見ると、どちらも0.2ぐらいです。20%ぐらいがAgeがNAだとわかります。
prop.test()関数でこの比率に違いがあるかどうかを確認します。
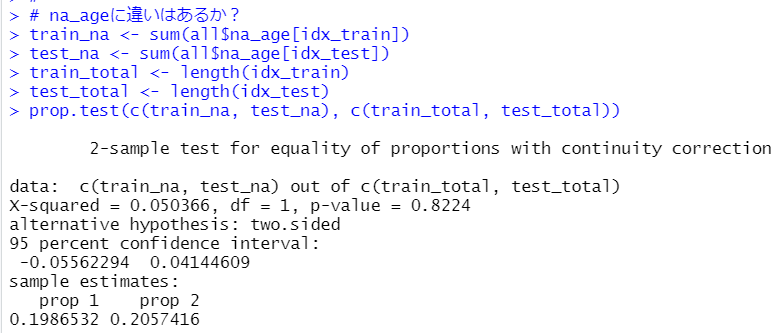
p-valueは0.8224と0.05よりもとても大きいので、trainとtestでAgeがNAの比率に統計的に有意な違いは無いようです。
na_ageを説明変数にして、Survivedを回帰分析してみます。

Interceptの係数は0.40616です。これはna_ageが0の人、つまりAgeのデータがある人の生存確率です。41%です。
na_ageの係数は-0.11238ですので、na_ageが1の人、つまりAgeのデータが無い人の生存確率は、0.40616 - 0.11238 = 0.29378%, 29%です。Ageのデータが無いという人は推測ですが、3等客室の人が多かったのではないでしょうか?
adj_ageの分析に移りましょう。これは連続変数なのでグラフで見たほうがわかりやすいかもしれないです。まずは、箱ひげ図でtrainとtestを比較してみます。値が0のデータはあらかじめ除いておきます。
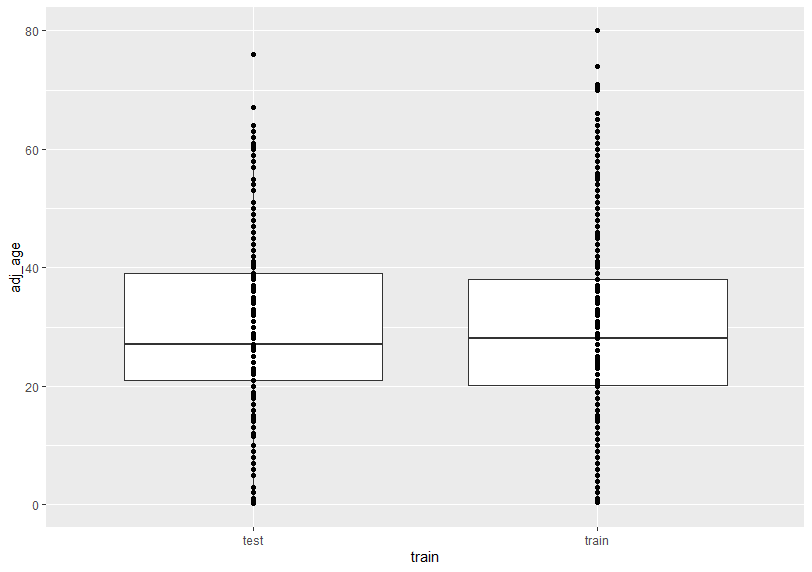
train, testであまり大きな違いは無いようですね。
ヒストグラムにしてみます。

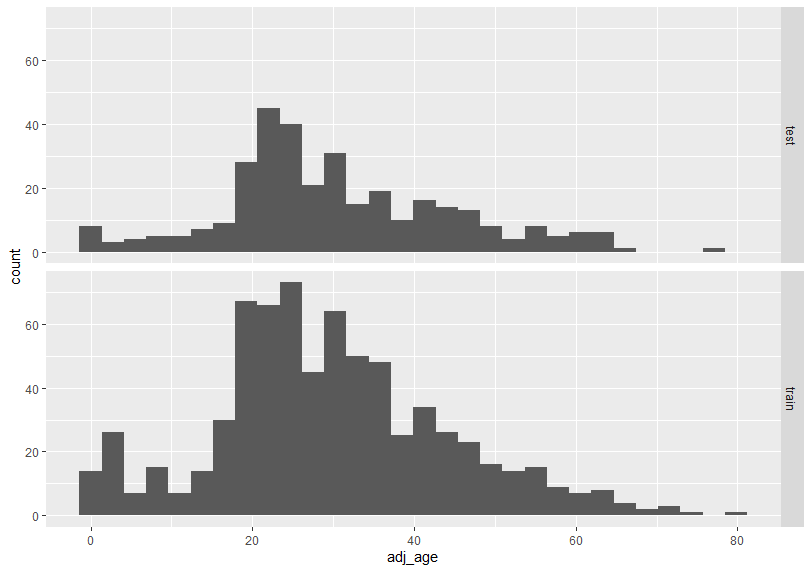
ヒストグラムの形状もあまり違いは無いようです。
t.test()関数で平均値に違いがあるかどうかを見てみます。

adj_ageが0を含むとき、含まないときの2つの場合の検定をしましたが、どちらもp-valueは大きくて、trainとtestで違いは無いようです。
それでは、adj_ageとSurvivedの関係を見てみましょう。
まずは単純に散布図を描いてみます。

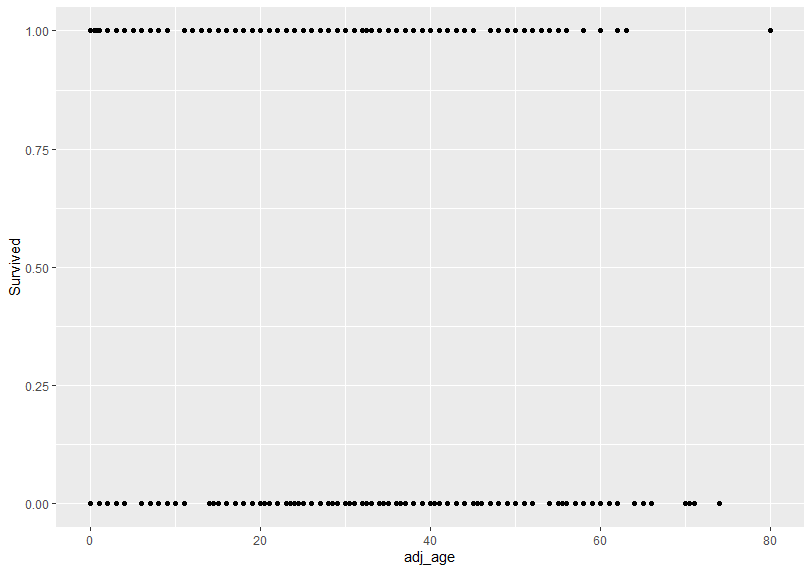
う~ん、これではよくわからないですね。10歳刻みでSurvivedの平均値を出してみます。
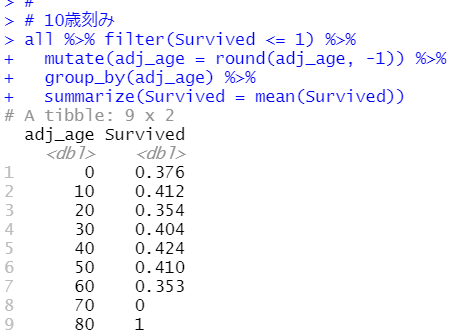
10代や40代、50代が比較的生存確率が高いようです。
棒グラフにしてみます。

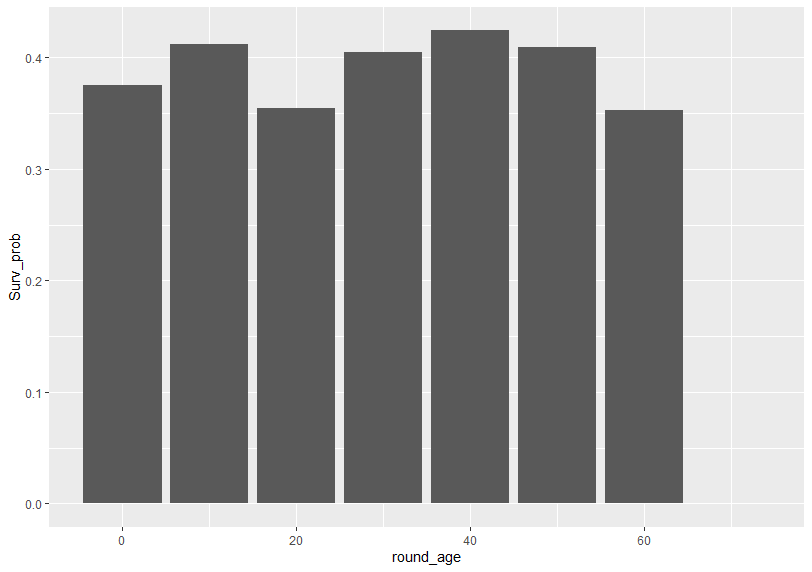
10代と40代という2つの年代が生存確率の高いところですね。年齢と生存確率は単純な直線的な関係ではないですね。
最後にlm()関数でSurvivedをadj_ageとna_ageで回帰分析してみます。上のグラフからわかるように単純な直線関係ではないようなのでadj_ageは多項式にします。
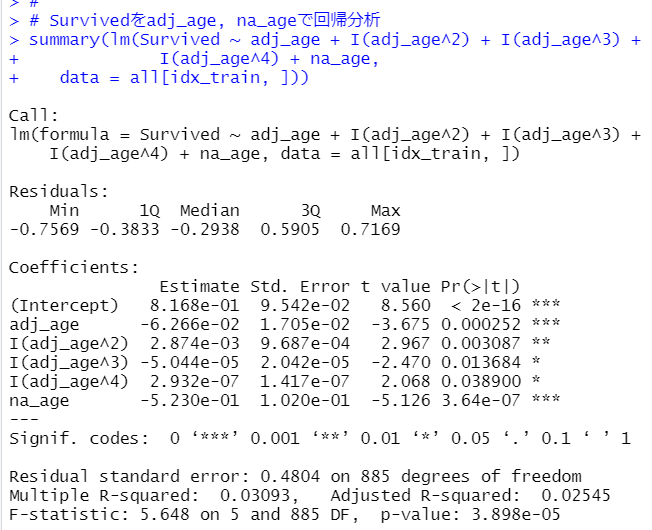
adj_ageは4乗の項目まで入れてみましたが、adj_ageからadj_age^4まで4つとも有意で、na_ageも有意です。
今回は以上です。
次回は、
です。
初めから読むには、
です。