
Photo by HyoSun Rosy Ko on Unsplash
今回は、Embarkedです。embarkという動詞は乗り込む、乗り出すという意味のようですので、乗り込んだ港ですかね。まずはNAが何個あるかを確認します。

NAは2個ありました。どういうデータがあるかhead()関数で始めの数個のデータを見てみます。
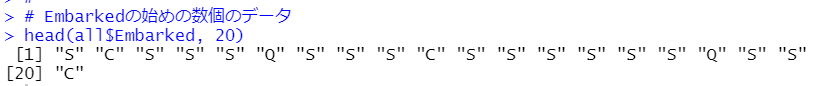
SやCやQなどアルファベット一文字のようですね。
table()関数で度数を見てみます。

Sが914で全体の半数以上なのですね。NAの2つもSだとみなしてしまいましょう。

それではtrainとtestでのEmbarkedの比率を比べてみます。table()関数で度数表を作ってから、prop.table()で比率の表に変換します。

trainのほうがSに集中していますね。カイ二乗検定でtrainとtestの度数分布に違いがあるのかどうか調べます。

p-value = 0.01442となっていますので、5%の有意水準でtrainとtestではEmbarkedの度数分布に違いが無いとは言えません。
グラフにしてみます。mosaicplot()関数を使いました。
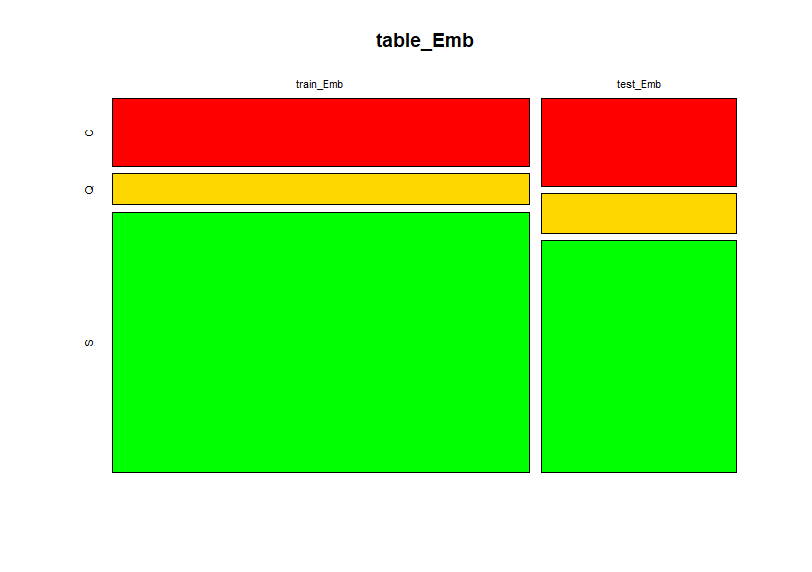
trainとtestで比率の違いがグラフになりました。
それでは、このEmbarkedとSurvivedの関係を見てみます。

Cの人が生存率が55.4%で一番高く、Sの人が33.9%で一番低いです。
Sをベースにしたダミー変数を作って回帰分析をしてみます。

EmbarkedがQなら1、そうでないなら0のダミー変数のemb_qと
Cなら1、そうでないなら0のダミー変数のemb_cを作りました。
この2つを説明変数に、Survivedを被説明変数にして回帰分析をします。

Interceptの係数、0.33901がEmbarkedがSの人の生存確率ですね。emb_qの係数のp値は0.382なので、EmbarkedがQの人とSの人では生存率に有意な違いは無いようです。
emb_cの係数のp値が0.01よりもうんと小さいので、Sの人とCの人では生存率に有意な違いはあるようです。
今回は以上です。
次回は
です。
初めから読むには、
です。