
Photo by Wolfgang Hasselmann on Unsplash
の続きです。
今回は単回帰分析(Sinple Regression Analysis)をRを使ってやってみます。
まず、前回作成したデータフレームから分析用のデータフレームを作ります。
複数年のデータでしたが、それから各都道府県別の平均値のデータフレームを作成します。

group_by()関数を使って pref 別にしてsummarize関数で各変数の平均値を計算しています。そして、mutate()関数で、Ed_p/Ed でP_ratio を作りました。
GdpをEdで回帰分析するモデルを考えます。
Gdp = beta_0 + beta_1 * Ed + u
というのが単回帰モデルです。
beta_0が切片、beta_1が Edの傾き、u は誤差項です。
まず、GdpとEdの散布図を見てみます。

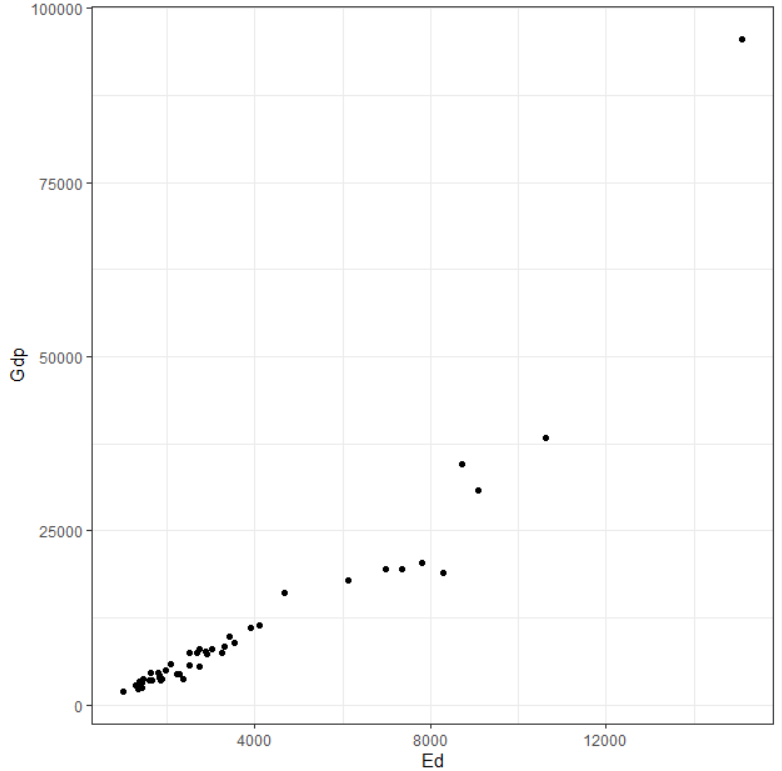
Edが大きいほど、Gdpが大きいですね。
lm()関数で回帰分析はできます。
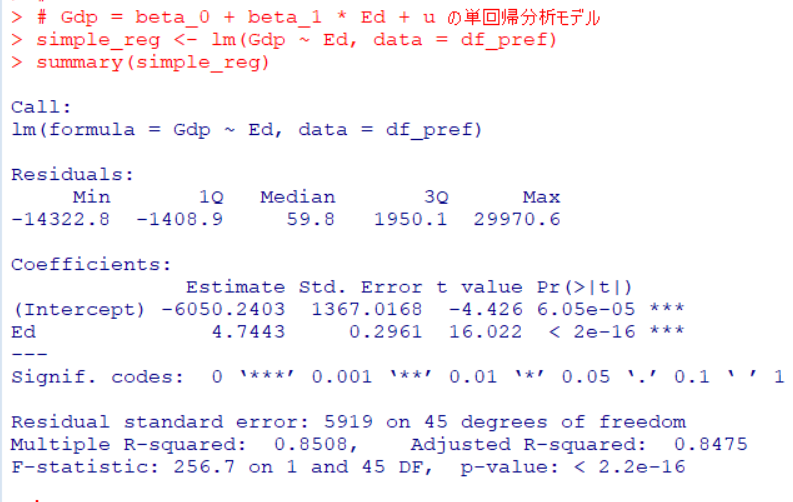
lm()関数で回帰分析モデルを作ったら、summary()関数でそのモデルを見ることができます。
Gdp = -6050 + 4.74 * Ed + u
という回帰式になりました。Edが1、単位は1億円ですから、Edが1億円増えると、Gdpは4.74億円増える、という意味になります。
単回帰分析の性質をいくつか確認していきます。
まずは、u, 誤差項の平均は0になる、という性質があります。
u は、resid()関数で求めることができます。
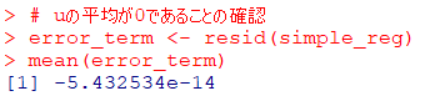
-5.4e-14ですからほぼ0です。
format()関数でe-14を使わないで表示してみましょう。

また、
Edとerror_temを掛け算したものの合計も0になります。

次は、
SST: total sum of squares
SSE: explained sum of squares
SSR: residual sum of squares
を計算します。これは説明をするより、実際に計算式を見るほうがわかりやすいと思います。
これらの計算には、Gdpの平均値と、回帰式から計算される推定Gdp, 誤差項が必要です。

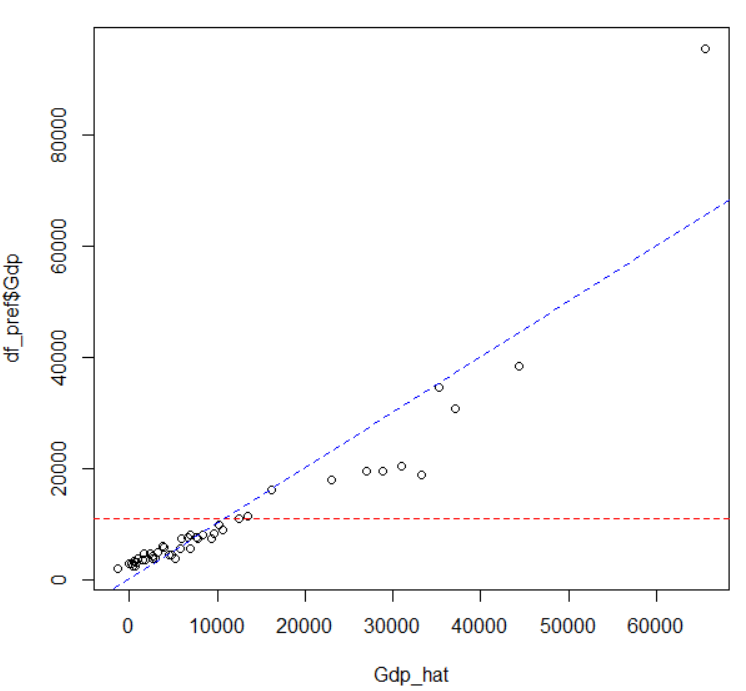
SSTから計算します。
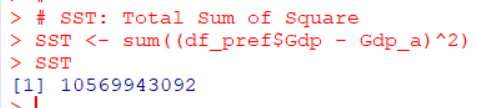
SSTは実際のGdpからGdpの平均値を引いて、2乗して、合計したものです。一口で言うと、Gdpの散らばり具合です。
SSRを計算します。
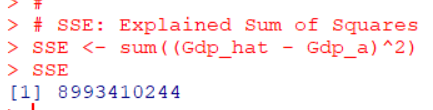
SSEは推計したGdpからGdpの平均値を引いて、2乗して、合計したものです。Gdpの平均値とGdpの推計値の平均値は同じなので、一口でいつと、推計したGdpの散らばり具合です。
SSRを計算します。

SSRは誤差項を2乗したものの合計です。一口で言うと、誤差項の散らばり具合です。
SST、SSE、SSRを計算しました。
SST = SSE + SSR という性質があります。確認してみます。

SSTもSSE + SSRも10569943092と同じ値ですね。
そして、R2, 回帰分析モデルがどれだけ実際のデータとフィットしているかを表す指標は、SSE/SST、または 1 - SSR/SSTで計算できます。
SSE/SST = Gdp推計値の散らばり具合/Gdp実際値の散らばり具合
1 - SSR/SST = 1 - 誤差項の散らばり具合/Gdp実際値の散らばり具合
です。誤差項の散らばり具合が小さいほど、R2は大きくなり、回帰分析モデルがより実際の値にフィットしていることになります。

どちらも0.8508476です。
そしてこれは、summary()関数で出力された、R-squaredの値と一致します。

今回は以上です。
次回は
です。
初めから読むには、
です。