
UnsplashのMaitheli Maitraが撮影した写真
の続きです。
前回は、回帰分析をしました。今回はその続きで、回帰分析したモデルの残差が均一分散かどうかをチェックします。
lmtestパッケージのbptest()関数で簡単にチェックできます。

bptest()関数は、Breush-Pagan Test を実行する関数です。

p値が0.3075と0.05よりも大きい値なので、均一分散だと言えます。
bptest()関数を使わない方法は、resid()関数で残差をだして、その2乗を説明変数で回帰分析します。
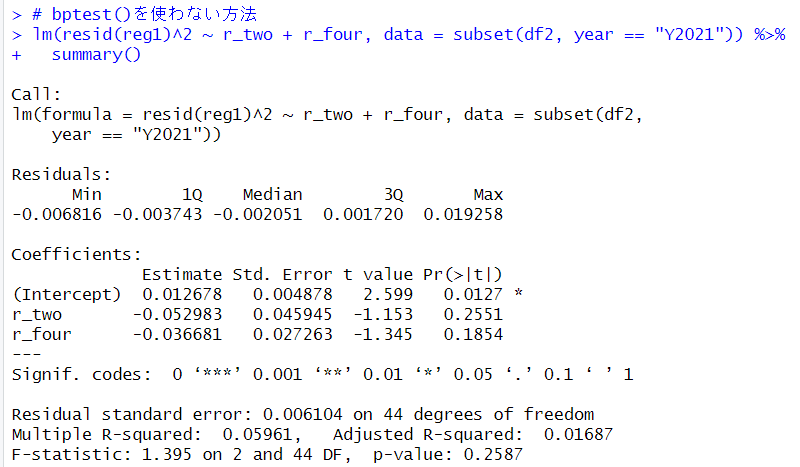
こちらの方法では、p値は0.2587です。こちらの方法でも、残差の2乗とr_two, r_fourは関連が無いことが確認できました。
reg3も調べてみます。

p値は0.3195と0.05よりも大きいので、reg3のモデルも均一分散と言えます。
bptest()関数を使わない方法でもやってみます。
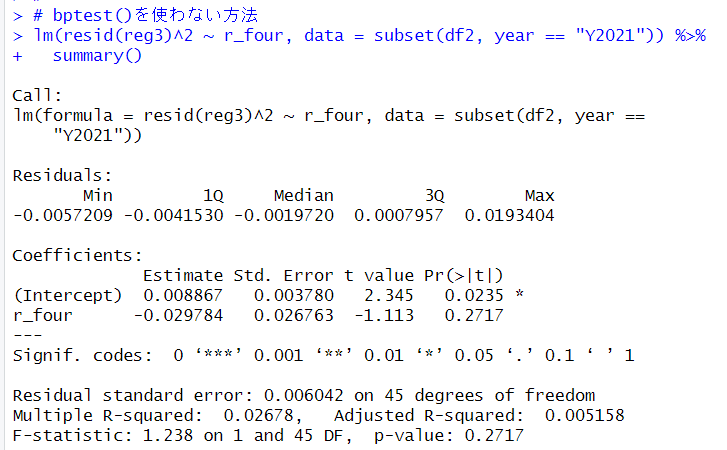
p値は0.2717なので、この方法でも均一分散であることが確認できました。
回帰分析の残差が均一分散か不均一分散かをテストする方法は、Breusch-Pagan Testの他に、White Testもあります。これは残差の2乗を回帰モデルから算出された予測値と予測値の2乗で回帰分析するものです。
これもbptest()関数で簡単にできます。

p値は0.2542なので、均一分散であると言えます。
bptest()関数を使わないでやってみます。

p値が0.2064なので均一分散であると言えます。
reg3のモデルでもWhiteの検定をやってみましょう。

p値が0.1557なので均一分散であると言えます。
bptestを使わないでWhiteの検定をやってみます。
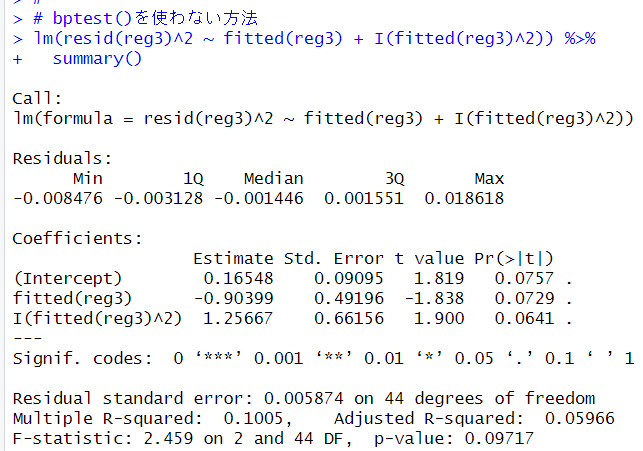
p値は0.09717と0.05よりも大きいので均一分散であると言えます。
次に残差の2乗とr_fourの散布図を描いて、本当に残差の2乗、つまり残差の分散がr_fourと関係していないかを視覚的に確認しましょう。
まず、moderndiveパッケージの読み込みをしておきます。

moderndiveパッケージのget_regression_points()という関数が便利です。
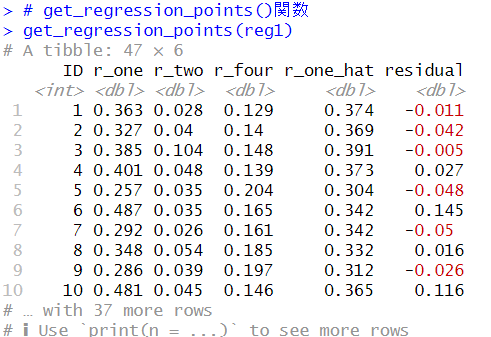
このように、回帰モデルのオブジェクトから、残差やy_hatも含めたデータフレームを作ってくれます。ここから散布図を作ります。

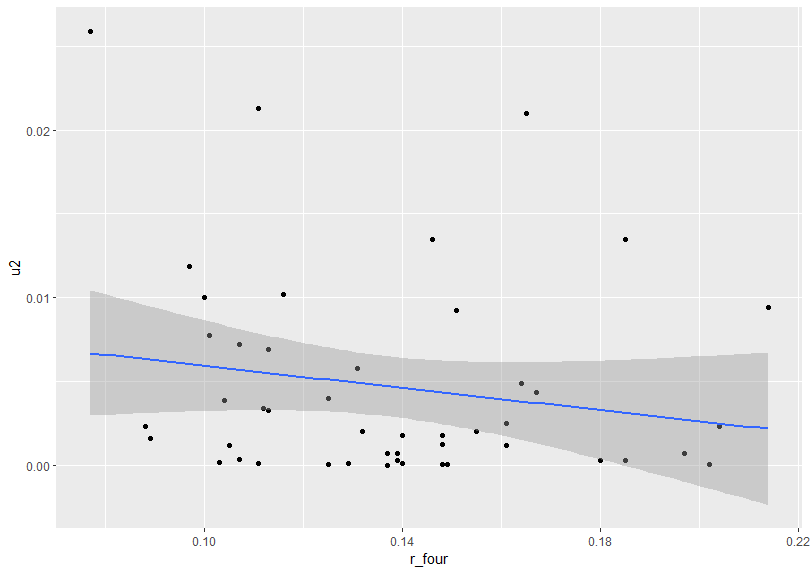
回帰直線の傾きは、右肩下がりでも右肩上がりでもとれるような感じです。
reg3でも散布図を描いてみます。

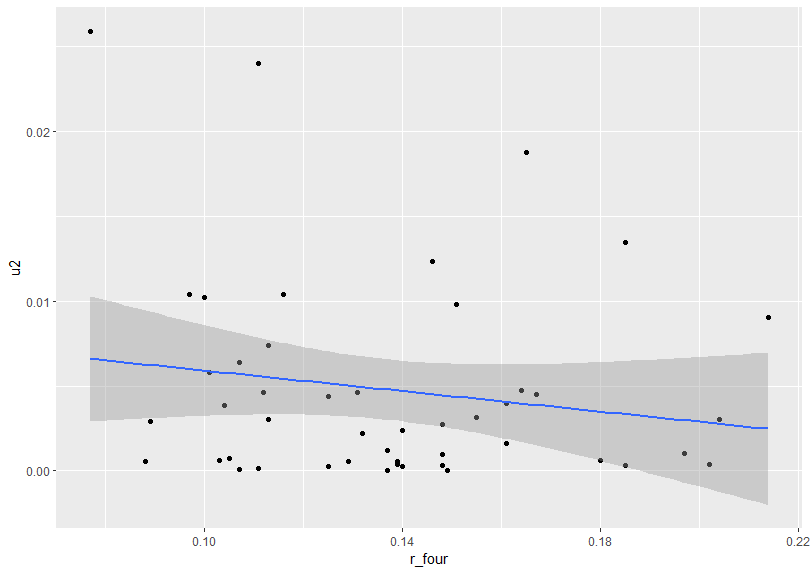
こちらも同じような散布図ですね。
moderndiveパッケージには、get_regression_table()という関数も用意されていて、
これで、回帰モデルの係数の信頼区間を見ることができます。
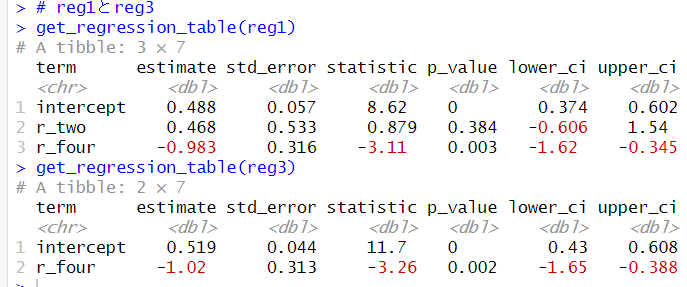
reg1のr_fourの係数の信頼区間は、-1.62 ~ -0.345で、reg3のほうは、-1.65 ~ -0.388です。
両者の信頼区間は、だいたい同じですね。
今回は以上です。
次回は、
です。
初めから読むには、
です。