
の続きです。
今回は、l_total: リフォーム・リニューアルの金額の対数変換値値をl_shotoku23: 平成23年基準の県民1人当たり所得の対数変換値で回帰分析してみます。1人当たり所得の所得が大きいほど、リフォーム・リニューアルの金額が大きいかどうかを調べてみます。
lm()関数で回帰分析してみます。

summary()関数でmodel1を表示してみます。

l_total = -23.283 + 3.8645(l_shotoku23) + u という結果です。
これは、shotokuが1%増えれば、totalが3.8645%増える、と解釈できます。
グラフで視覚化してみます。
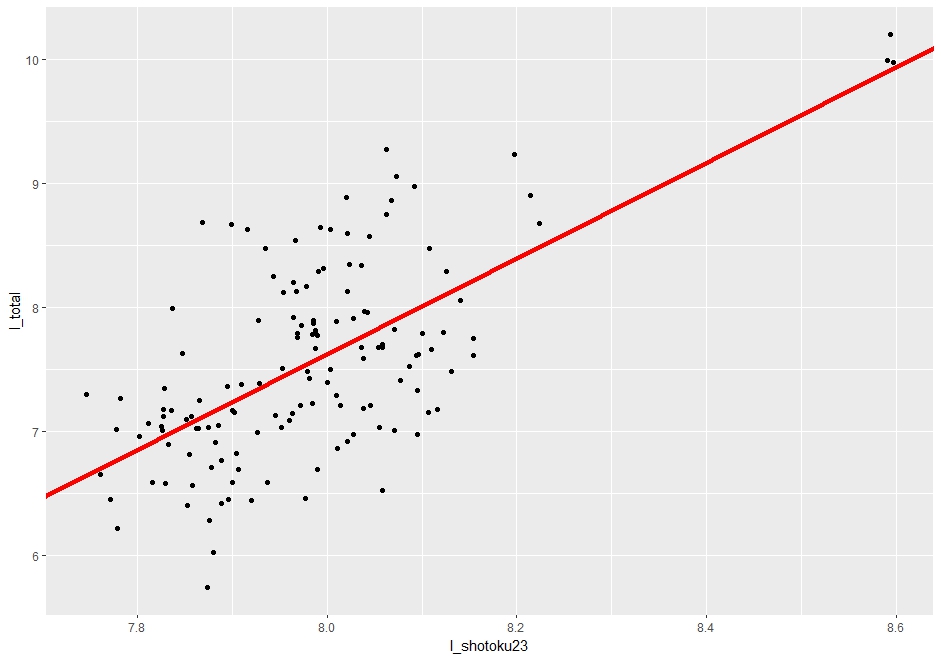
散布図を見ると、確かに右肩上がりになっています。
このモデルに、yearを加えるとどうなるでしょうか?

update()関数でmodel1にyearを加えてみました。
summary()関数で表示してみます。
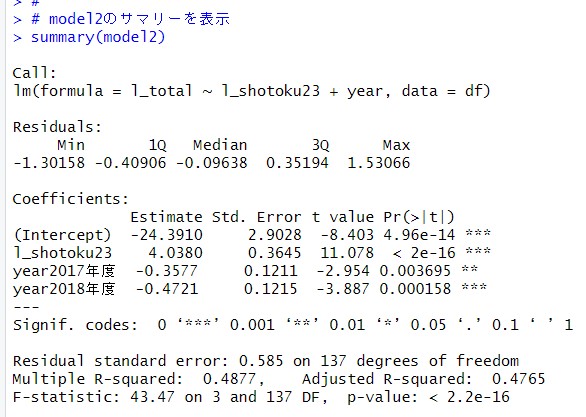
l_shotoku23の係数が4.0380になりました。
yearを入れたこのモデルは、l_shotokuの傾きは一緒で、2016年度、2017年度、2018年度と切片が違うモデルです。
これもグラフにしてみたいと思います。
これは、moderndiveパッケージのgeom_parallel_slopes()関数を使ってみます。

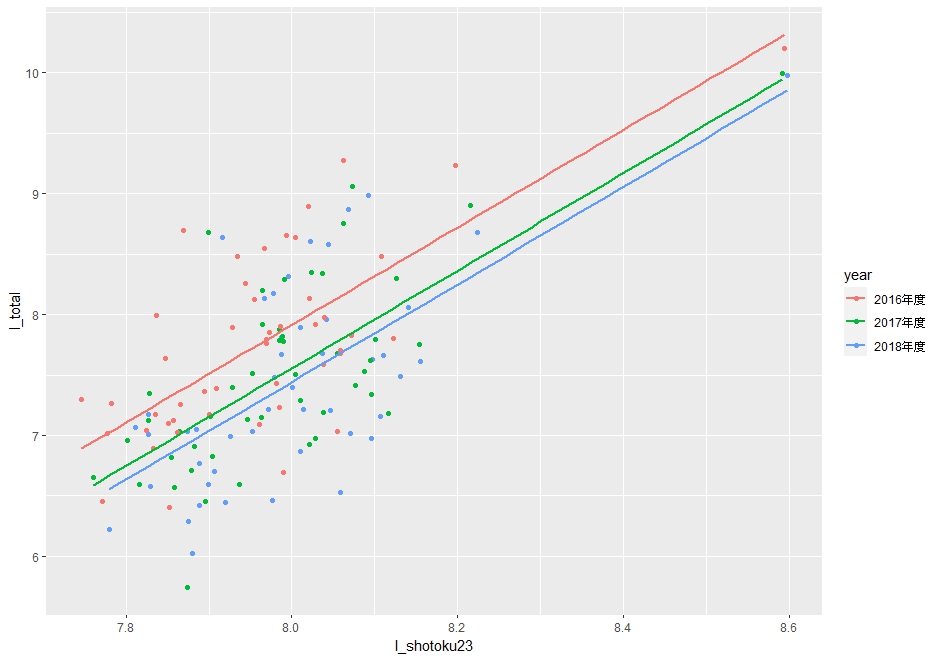
2016年度が一番上に回帰直線があります。
このmodel1とmodel2では統計的に有意な違いがあるのかどうか、anova()関数で確認します。
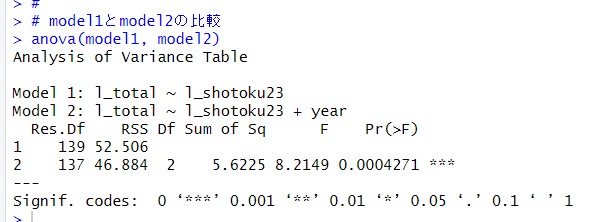
p値が0.0004271となっているので、model1とmodel2は統計的に有意な違いがあります。つまり、model1にyearを加えた意味は有った、ということです。
今度は、年度ごとに傾きが違うモデルを考えてみます。
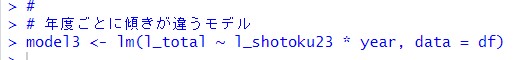
l_shotoku23 * year と + ではなくて、* を使うと切片だけでなくて、傾きも違うモデルになります。
サマリーを表示してみます。
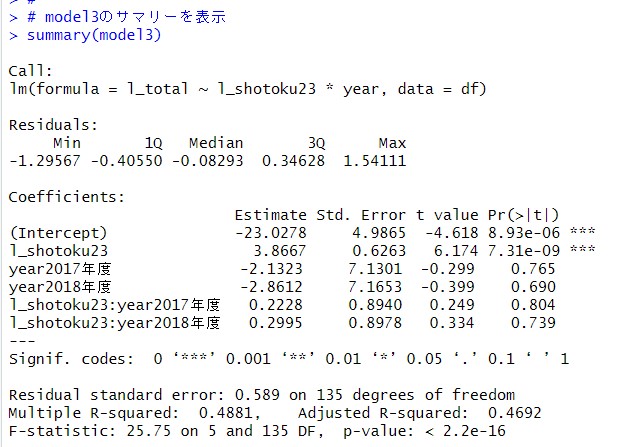
l_shotoku23の係数が、3.8667になっています。これは、2016年度の傾きです。
2017年度の傾きは、これにl_shotoku23:year2017年度の0.2228を足して、
3.8667+0.2228=4.0895になります。
2018年度の傾きは、3.8667+0.2995=4.1662となります。
傾きが年度が増えるごとに急になっています。
これもグラフにしてみます。geom_smotth()関数で視覚化できます。

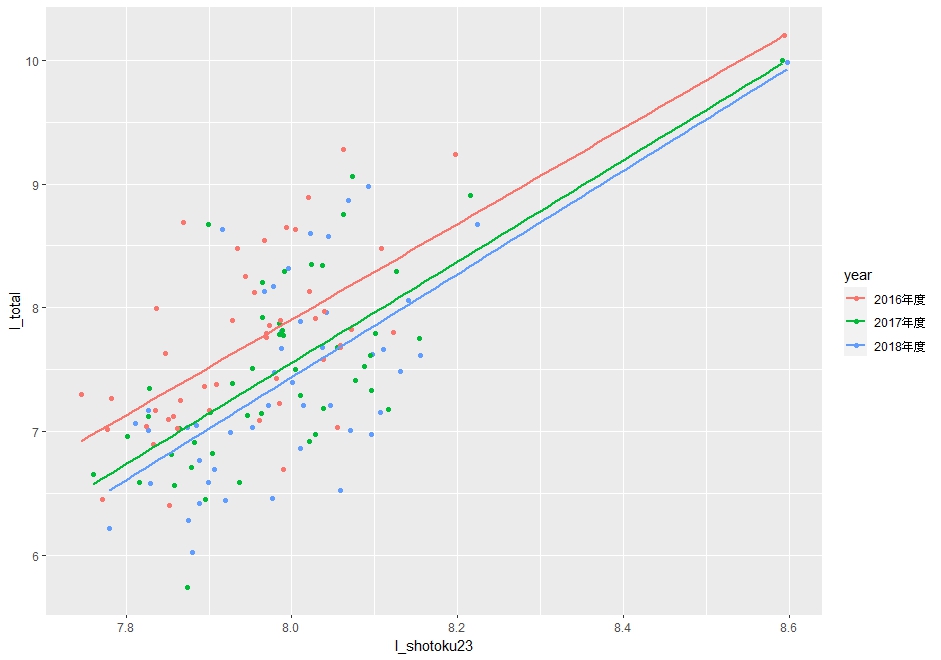
傾きの違いは、あまり感じられないですね。
anova()関数で、model2とmodel3を比較してみます。
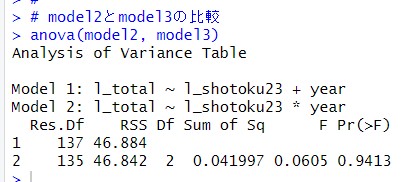
p値が0.9413ですから、model2とmodel3で統計的に有意な違いは無いということです。つまり、傾きを年度ごとに変える意味は無いですね。
こんどは、model2にprefを加えてみます。都道府県ごとにも切片を変えるということです。

summary()関数でmodel4をみてみます。
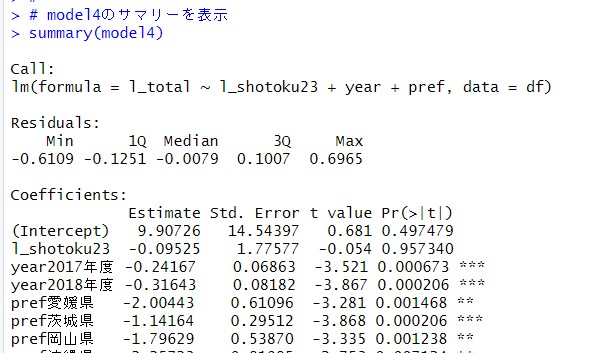
中略
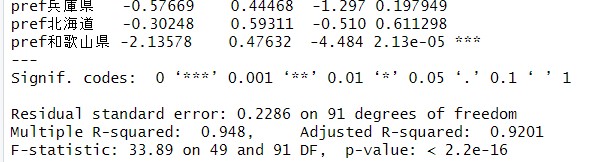
l_shotoku23の係数が-0.09525とほとんど0に近いマイナスになりました。p値も0.957340となっているので、prefを考慮すると、l_shotoku23はl_totalとは無関係ということですね。
anova()関数で、model2とmodel4を比較してみます。
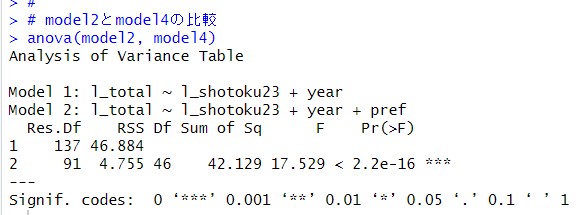
p値は2.2e-16とゼロといってよいぐらい小さい値です。moel2にprefを加えてmodel4を作成した意味はあった、ということですね。
今回の結論としては、都道府県の違いを考慮しないと、県民1人当たり所得が多いほどリフォーム・リニューアルの金額も多い。都道府県のごとに見ると、県民1人当たり所得とリフォーム・リニューアルの金額は無関係、ということでした。
今回は以上です。
次回は、
です。
初めから読むには、
です。