
の続きです。
前回は、各変数の上位と下位の都道府県を見てみました。
今回は2つの変数間の相関係数について見てみます。
まず。データフレームを世帯の種類が「総数」だけにします。世帯の種類には注目しないで、総数だけで考えようということです。
たくさん変数がありますが、必要な変数、shotokuとl_から始まる変数だけにします。
as.matrix()関数で、データフレーム型からマトリックス型に変換しました。
列名を都道府県名にします。
cor()関数で相関係数マトリックスを表示します。
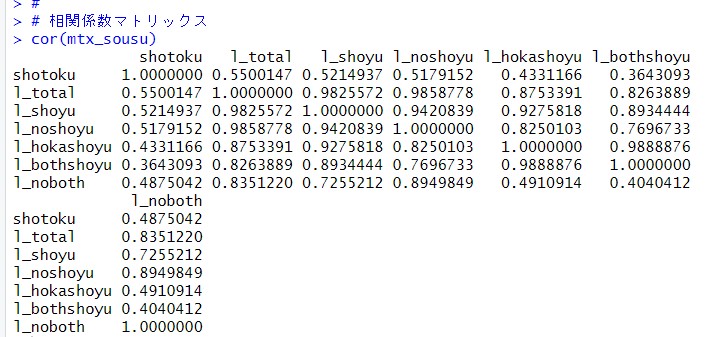
l_がつく変数どうしは、l_nobothとl_hokashoyu, l_nobothrとl_bothshoyuが0.5以下の他はどれも0.7以上で高相関です。
shotokuとl_のつく相関は、l_totalが一番相関があって、0.55ですが他はそれ以下です。
pairs()関数で散布図マトリックスを描けます。

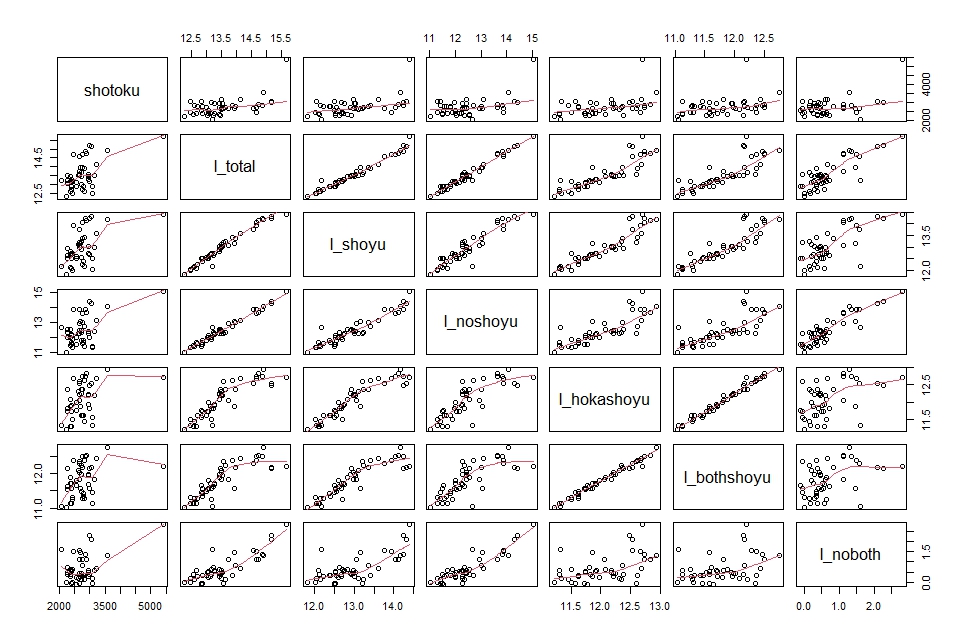
shotokuも東京都を除けば、他の変数と相関が強く出ているような気がします。
確かめてみます。
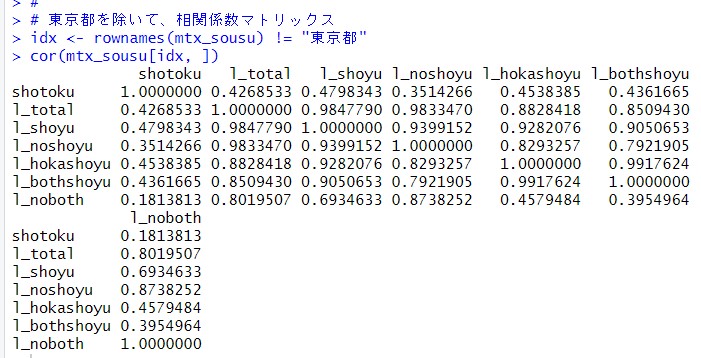
idx <- roenames(mtx_sousu) != "東京都" で東京都以外はTRUEになるロジカル型のベクトルを作り、それを利用しました。
直感に反して、東京都を除外したほうが、shotokuと他の変数の相関係数は低くなりました。
cor.test()関数で2つの変数が有意に相関しているかどうかを検定できます。
ここでは、一番相関の低い、shotokuとl_bothshoyuを調べてみましょう。
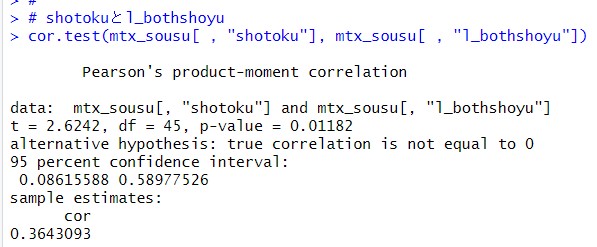
p-valueが0.01182と0.05以下なので、統計的に有意に相関関係があると言えます。
相関関係の95%信頼区間は、0.086 ~ 0.589となっています。
cor.test()関数は理論ベース、公式で信頼区間やp値を算出します。
こんどは、シミュレーションベースで信頼区間やp値を算出してみます。ブートストラップ法というですかね。
まずは、作業しやすいようにデータフレームを作ります。
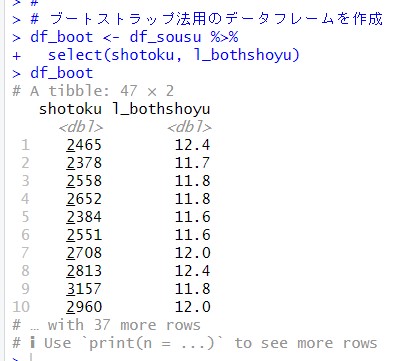
ブートストラップ法は、
「この47個の観測値からランダムに47個の観測値を抜き出し、相関係数を計算」
という作業を1000回とか1万回とか繰り返します。
そうすると、相関係数の値が1000個とか1万個とか得られますので、その中の95%の範囲や、0以上の比率を計算する、という方法です。
言葉よりもコードのほうがわかりやすいかもしれません。

soukanのヒストグラム描いてみます。

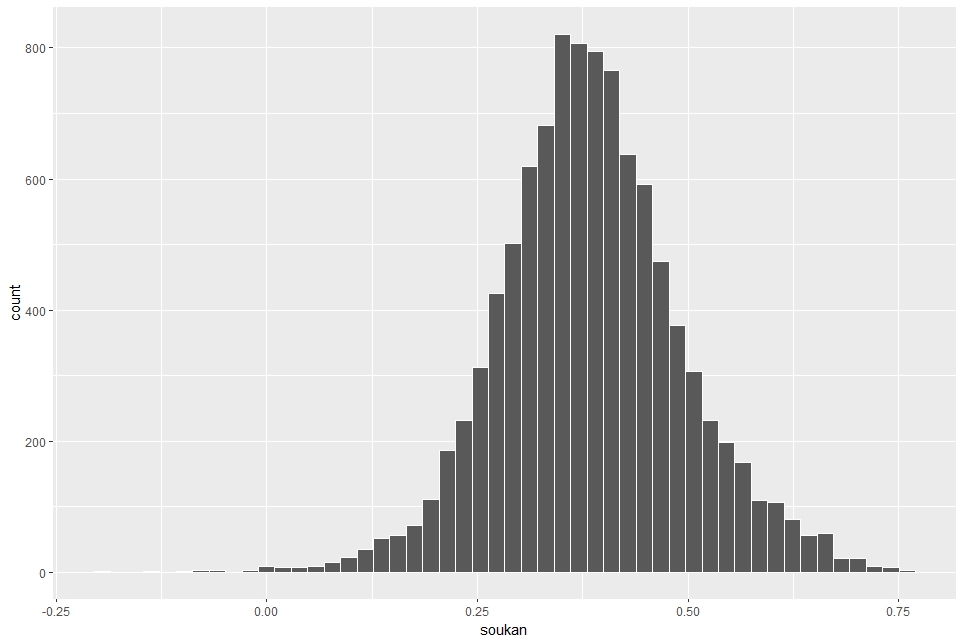
相関係数が0以下の場合もあったようですが、おおむね0.36という本来の相関係数を中心に分布しています。
2.5パーセンタイル値と97.5パーセンタイル値を算出すれば、95$信頼区間が求まります。
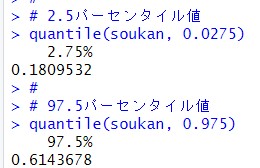
ブートストラップ法での95%信頼区間は、0.18~0.61です。
理論ベースの信頼区間とは少し違いますね。
上のヒストグラムに理論ベース、シミュレーションベースの信頼区間を重ねてみます。

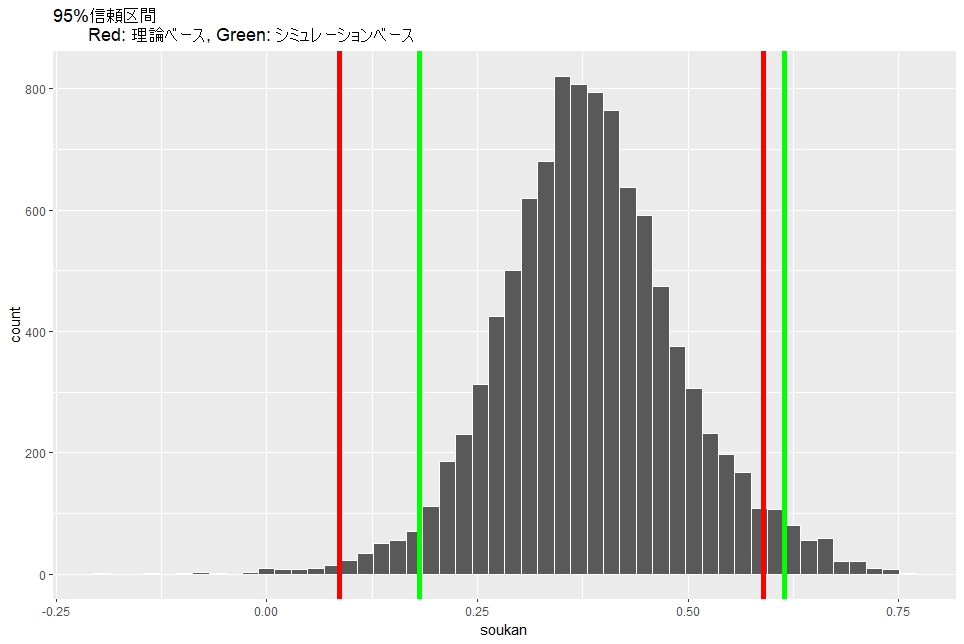
今回は以上です。
次回は、
です。
初めから読むには、
です。