
Photo by Ahsen Sunay on Unsplash
の続きです。
前回は2015年だけのデータを使って回帰分析しました。
今回は2010年のデータも使って回帰分析してみます。
まず、2010年と2015年だけのデータフレームを作成します。

d10というダミー変数を加えています。これは2010年ならば1、2015年ならば0という変数です。
このd10というダミー変数を入れて前回と同じような回帰分析をします。
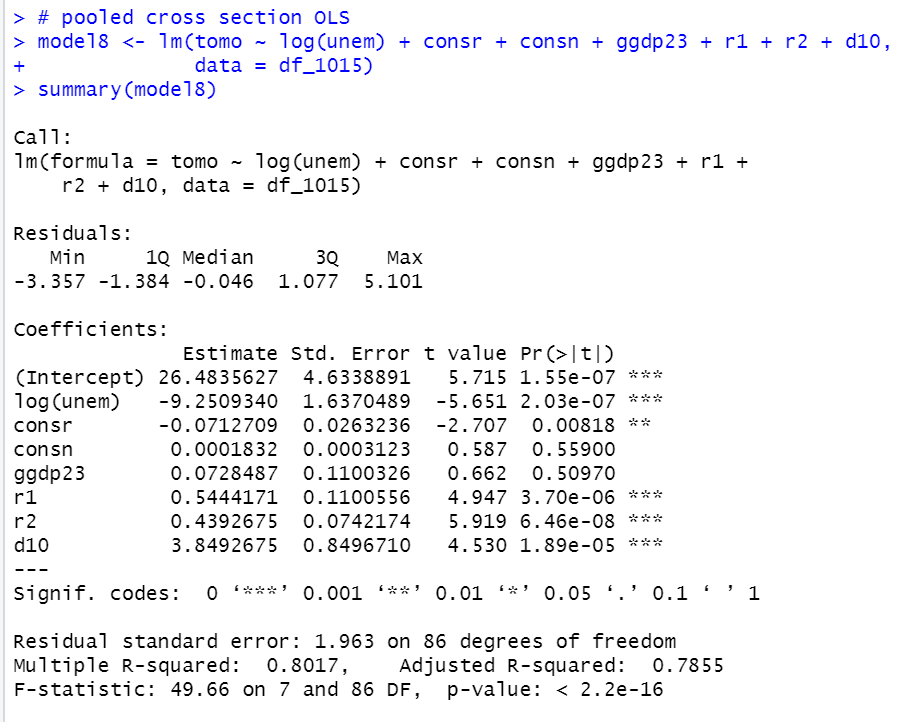
log(unem)の係数は-9.2で統計的に有意です。unem: 完全失業率が1%高いとtomo: 共働き世帯割合(%)は0.92ポイント低下するということです。d10の係数が3.85でこれも統計的に有意です。d10が1、つまり2010年のほうがtomo: 共働き世帯割合(%)が3.85高いということです。
この回帰分析モデル(model8)と前回の回帰分析モデル(model7)を比較してみましょう。
stargazerパッケージを読み込みして、stargazer()関数を使うと論文に出てくるような形式で出力できます。

係数が大きく変わった変数は、ggdp23ですね。2015年だけのデータのmodel7では0.330で10%水準で有意でしたが、2010年も加えたデータのmodel8では0.073とかなり小さくなって有意ではなくなりました。
consr: 人口集中地区面積比率(%)がmodel7では有意ではありませんでしたが、model8では1%水準で有意になりました。人口集中地区面積比率が高いほど、共働き世帯割合は低いという解釈です。
model8はpooled cross section data という単純に複数年のデータがあるクロスセクションデータの回帰分析でした。
こんどは、各年のクロスセクションデータが同じ観測対象を観察しているパネルデータとして回帰分析をしてみましょう。
まず、plmパッケージを読み込みして、pdata.frame()関数でパネルデータフレームを作成します。
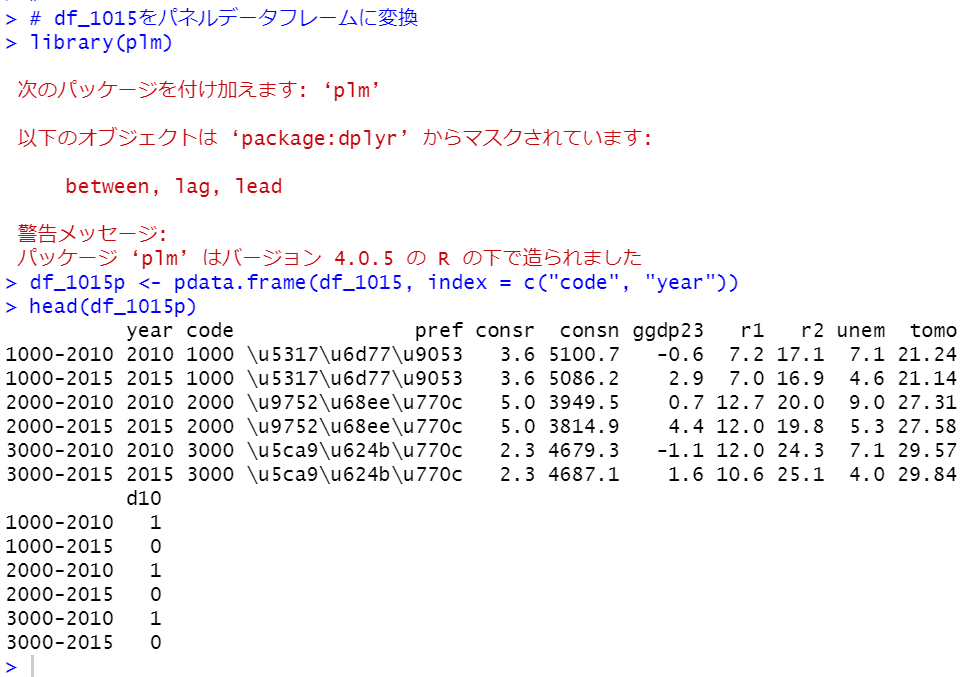
あれれ?prefが文字化けしてしまいましたね。。しょうがないので削除します。その後にpdim()関数でパネルデータフレームになっているかどうか確認します。
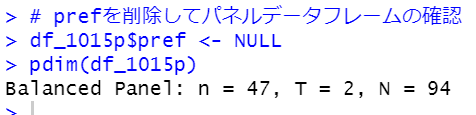
Balanced Panelと表示されています。これは、各年の各観測対象のデータがちゃんと揃っているということですね。n = 47なので観測対象は47(都道府県なので47ですね)、T=2なので、観測年は2年(2010年と2015年ですね)、N=94は47x2です。94行データがある、ということです。
今回は、パネルデータフレーム分析の手法の一つ、First Differenced Estimatorをやってみます。
これは、
y_it = beta_0 + beta_1 * log(unem)_it + beta_2 * consr_it + beta_3 * consn_it + beta_4 * ggdp23_it + beta_5 * r1_it + beta_6 * r2_it + a_t + u_it
iは観測対象(今回は1 ~ 47)、tは観測年(今回は1, 2)
というモデルを考えます。a_tというのが個々のi、今回は都道府県に特有で、このモデルではとらえることのできないt=1, 2で変わらない特性を表しています。u_itは誤差項です。
こういう推計式があるとき、t=2のときの式からt=1のときの式を引くと、
Δy_it = Δy_it - Δy_it-1
= beta_1 * Δlog(unem)_it + beta_2 * Δconsr_it + beta_3 * Δconsn_it + beta_4 * Δggdp23_it + beta_5 * Δr1_it + beta_6 * Δr2_it + Δu_it
となってa_tが消える、という理屈です。
plm()関数で、model = "fd"とすると実行できます。
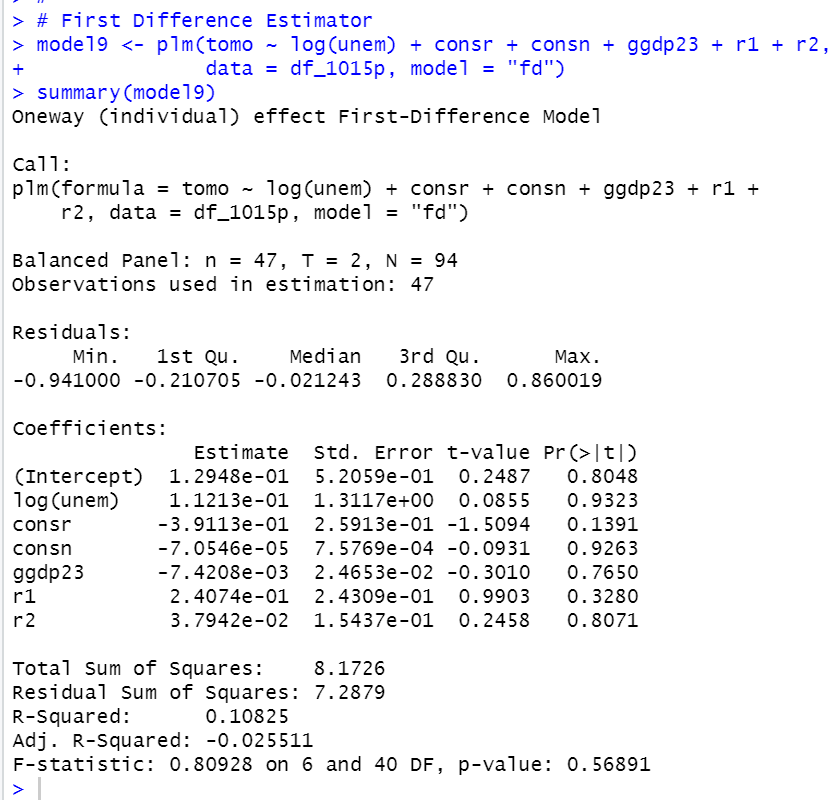
あらら。。全部の変数が統計的に有意ではなくなってしまいましたね。。
これは、モデルから消去されたa_iが共働き世帯割合に大きな影響を及ぼしている、ということでしょうかね?よくわからないですが。。
今回は以上です。
次回は
です。
初めから読むには、
です。