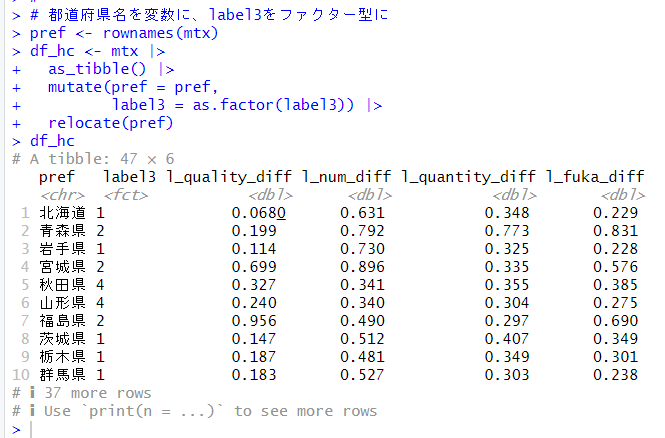
Bing Image Creator で生成: blue sky, green grass, white clouds, some flowers, cheerful image photo
の続きです。
今回は、R の rpart パッケージで決定木モデル (decision tree model) で予測をしてみます。
を参考にしてみました。
まずは、rpart パッケージと rpart.plot パッケージを読み込みます。

つぎは、rpart() 関数で剪定前の決定木 (decision tree) を生成します。

rpart.plot() 関数で生成された決定木 (decision tree) を描いてみます。


枝がいっぱいの複雑な木ですね。これだと、新しいデータでは上手く予測できないかもしれませんので、剪定をします。
cp というパラメータを使って剪定しますが、どのくらいの cp がいいかを見るために、plotcp() 関数を使います。

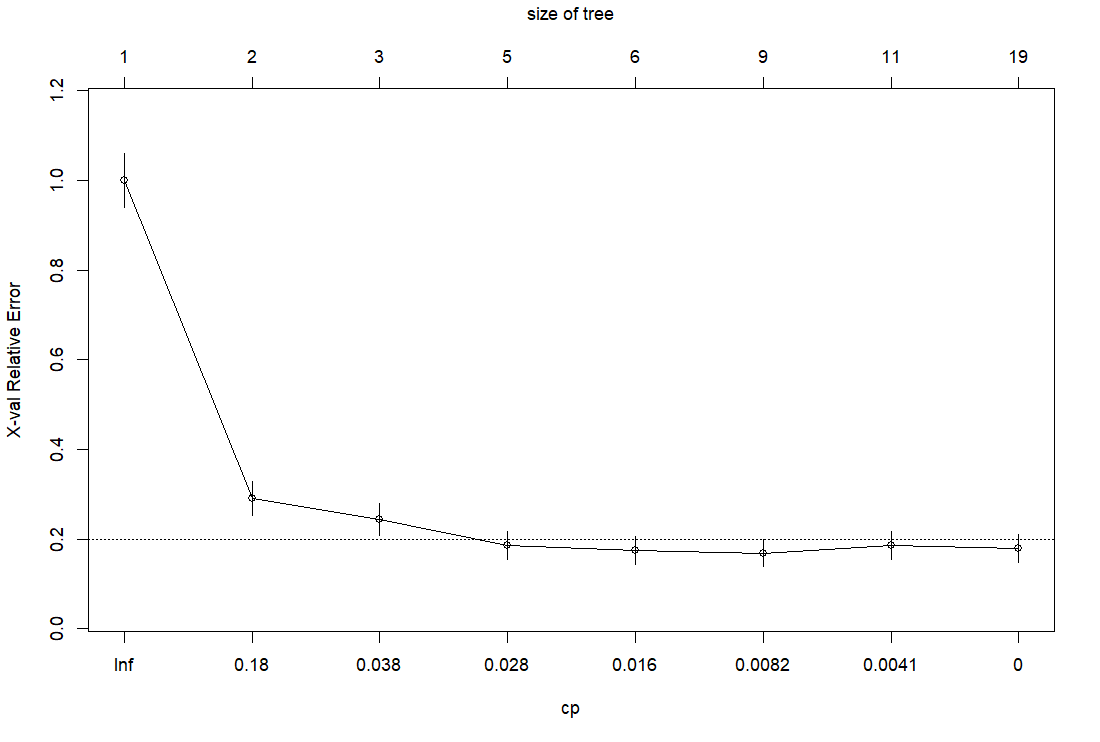
cp = 0.028 のところで、水平線を下回っていますので、cp = 0.028 で剪定します。
prune() 関数を使います。

こうして選定した決定木 (decision tree) を描いてみましょう。
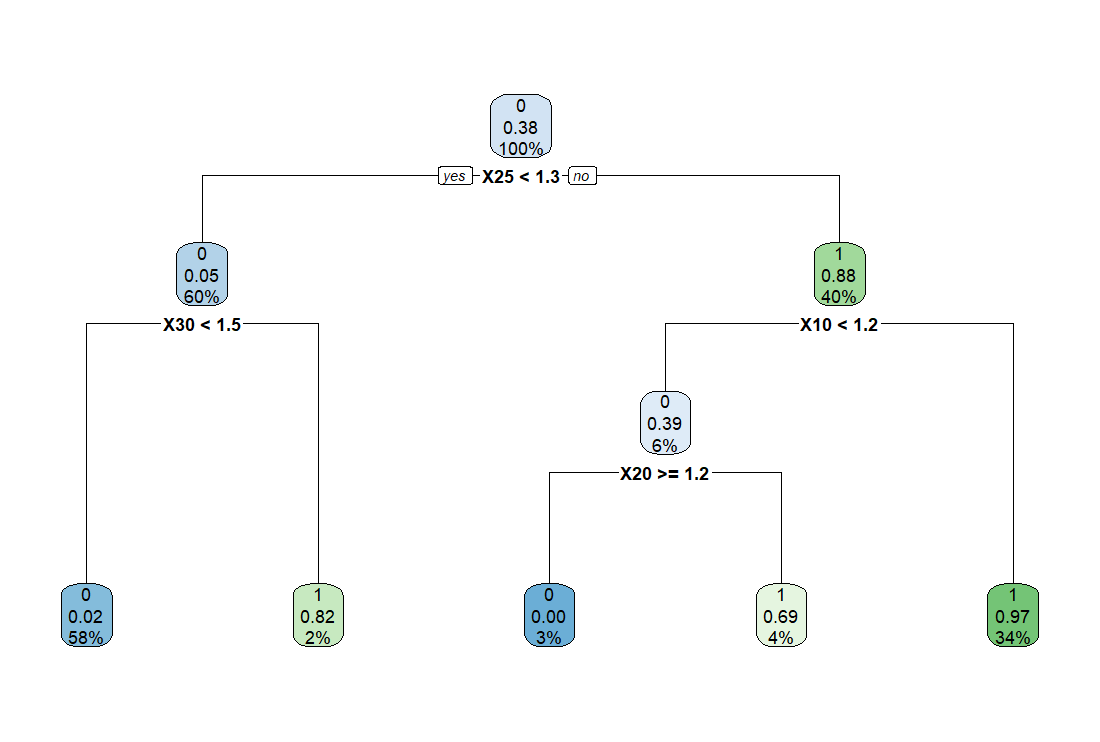
だいぶスッキリしました。X25 < 1.3 で X30 < 1.5 だと M = 0 となります。この決定木 (decision tree) の一番左です。
X25 > 1.3 で X10 > 1.2 だと M = 1 となります。この決定木 (decision tree) の一番右です。
このモデルで予測をしてみます。

正解率は、92.1% でした。
ロジスティクス回帰や LASSO 回帰よりは正解率が悪いですね。
今回は以上です。
初めから読むには、
です。