今回は、Kaggle の Titanic の Competition に参加してみたので、その報告です。

https://www.kaggle.com/c/titanic
とうもので、簡単に言うと、タイタニック号の乗客のデータを使って誰が生存して、誰が死亡したかを判別するというものですね。
マシンラーニングとか高度なテクニックは、私はまだ無いので、簡単なカイ二乗検定を応用して判別式を作ってみました。
それでは、具体的にどのようにしたかを報告します。
まずは、訓練用のデータファイルを読み込んで、R言語に読込ませます。summary関数でどんなデータがあるかを確認しました。
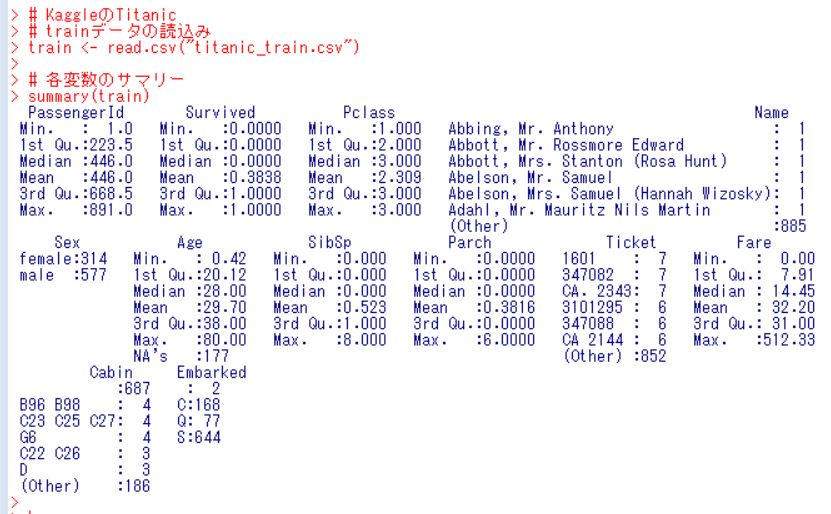
1番目の変数:PassengerId は乗客番号ですね。最大値が 891 ですから、891人のデータです。
2番目の変数:Survivedというのが、生存=1, 死亡=0 となっていて平均値が 0.3838 となっているので、生存率は 38% とわかります。
Survived をもう少し細かくみてみましょう。まず、str関数でデータ型を確認し、そのあとに、hist関数でヒストグラム、plot関数とdensity関数でカーネル密度グラフ、plot関数とsort関数で小さい順グラフ(この小さい順グラフって正式にはなんて言うのでしょうか?)を描いてみます。

データ型は、int(整数)ですね。
hist関数でヒストグラムを描きます。

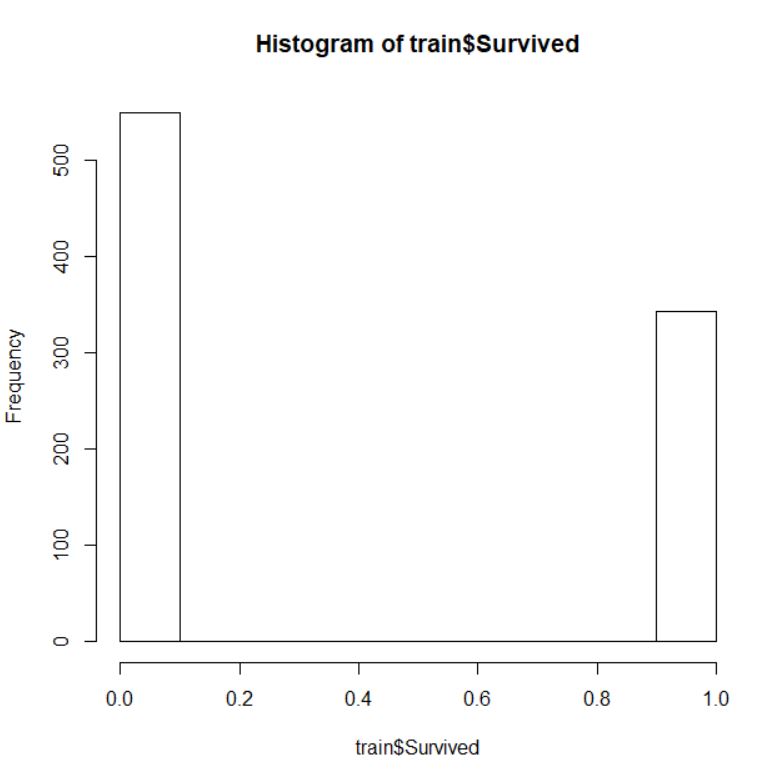
0 と 1 に分かれています。カーネル密度グラフはどうでしょうか?

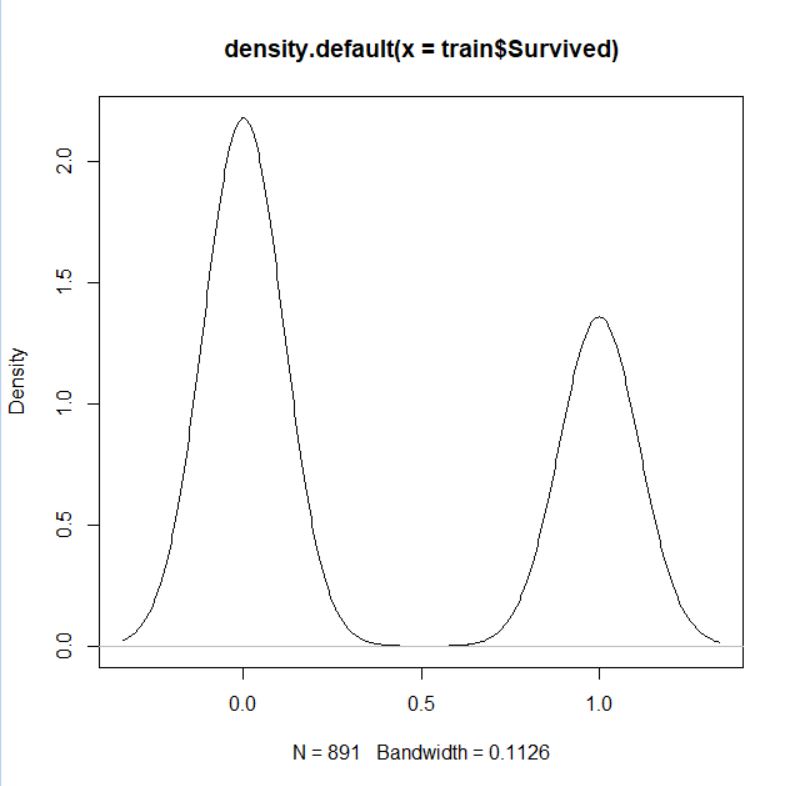
山が 0 と 1 のところに2つあります。小さい順グラフを描きます。

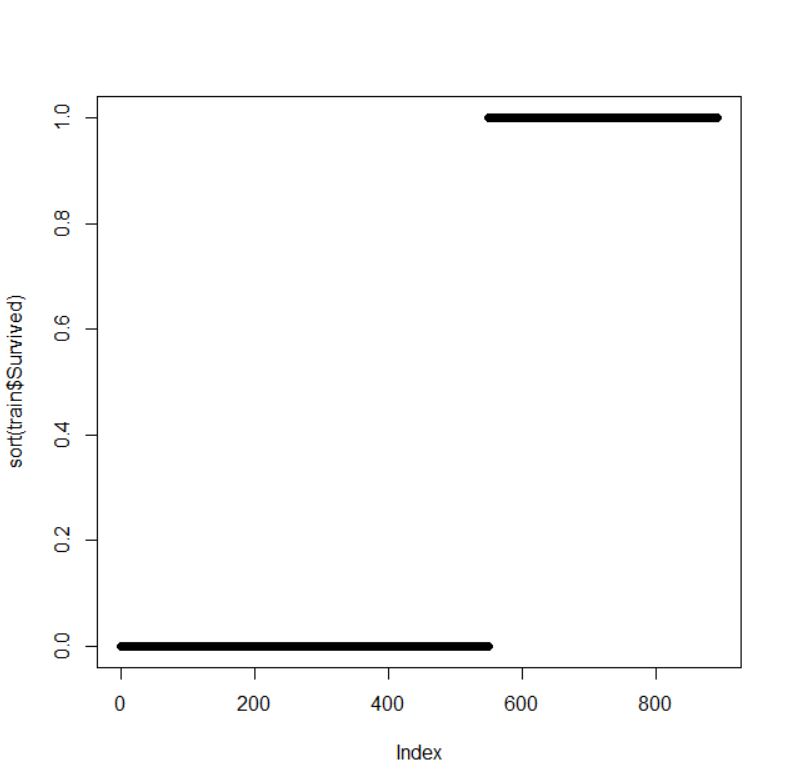
0 と 1 の値しかないことが確認できます。なので、データ型を factor型に変換して、0 を dead, 1 を arrive と名付けます。

次に、Pclass のデータ型を str関数を使って確認します。

整数ですね。三つのグラフで様子を視覚化しましょう。

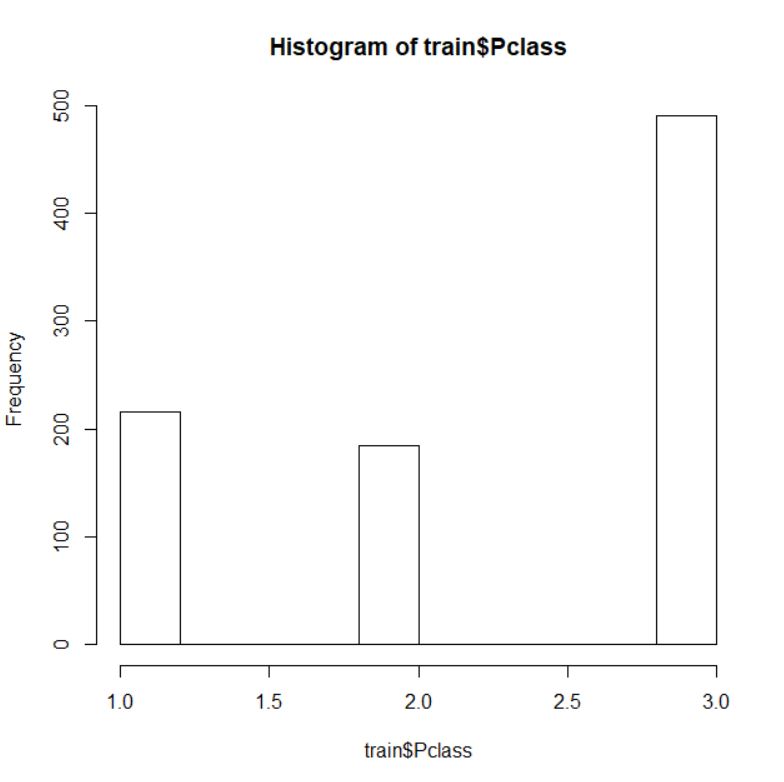

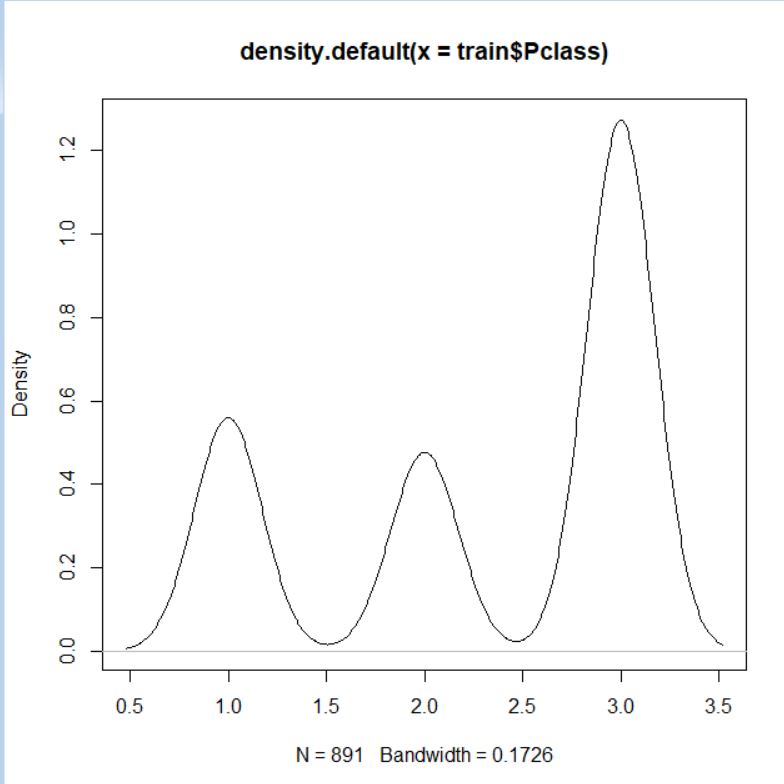

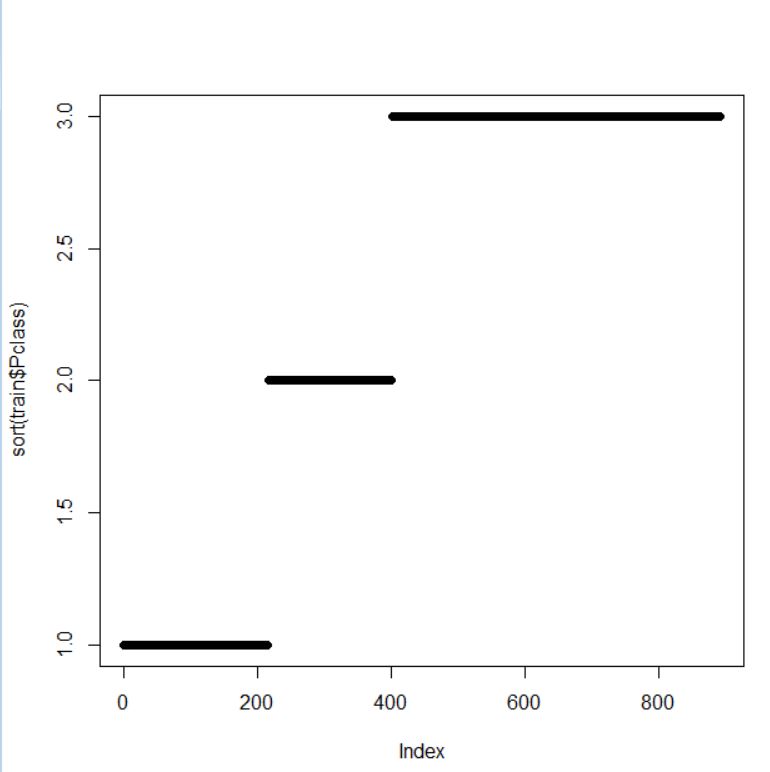
Pclass は 1, 2, 3 の3つの値しかとらず、3 が一番多いことがわかりました。そこで、Pclass を 3 と non-3 の2つのグループの factor に変換します。
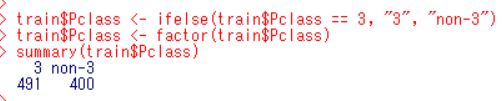
3 が 491人、non-3 が400人です。
Name のデータ型を確認します。
Name は乗客の名前ですよね。データ型は factor で level が 891 もあります。これは分析に使わないと判断しました。
Sex を調べましょう。

Sex は factor で、female が314人、male が577人です。
Age を調べます。

Age は number型ですね。年齢ですからね。int(整数)でないのが以外です。ヒストグラム、カーネル密度グラフ、小さい順グラフを描きます。

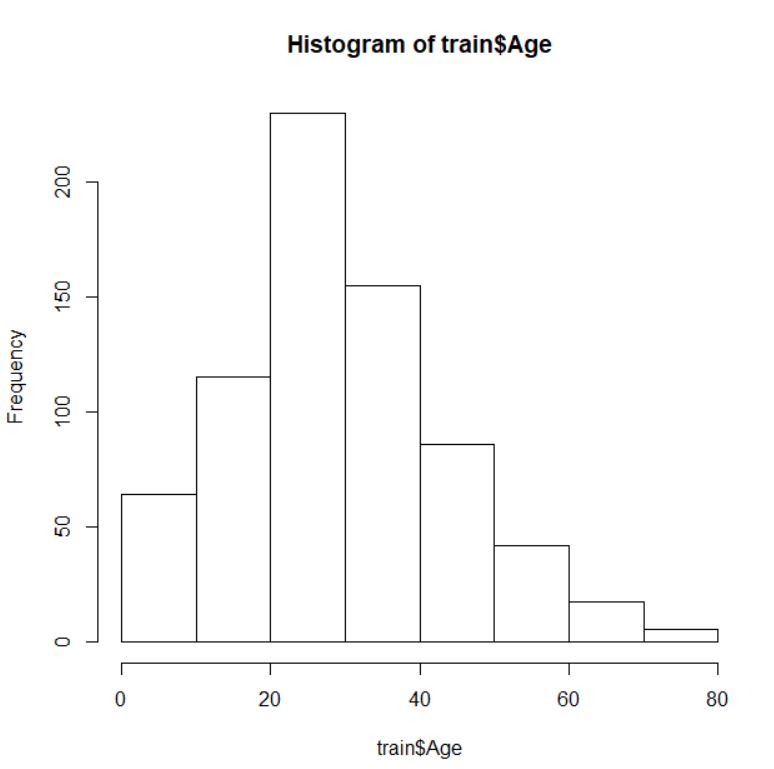

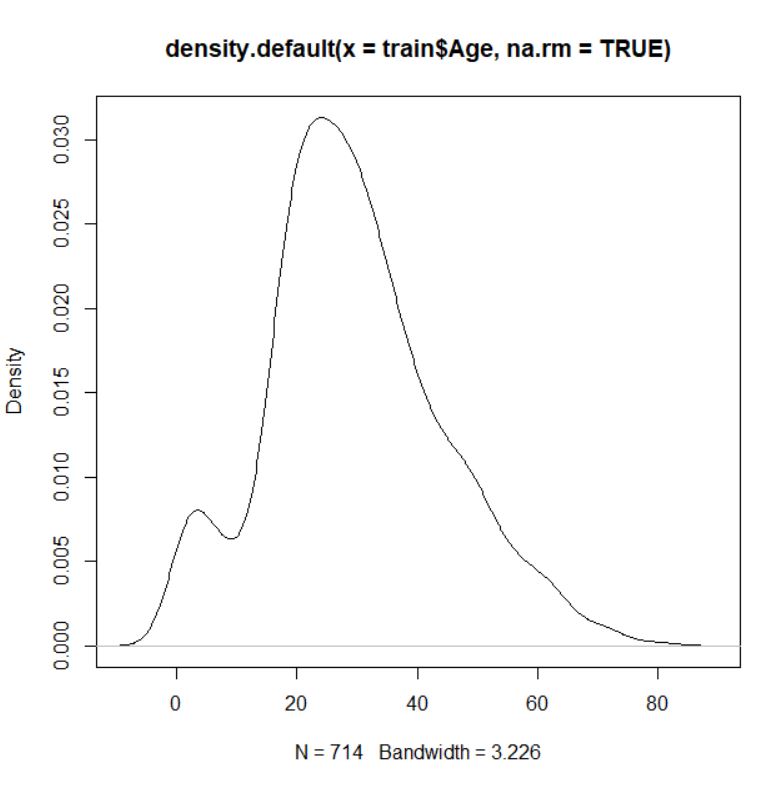

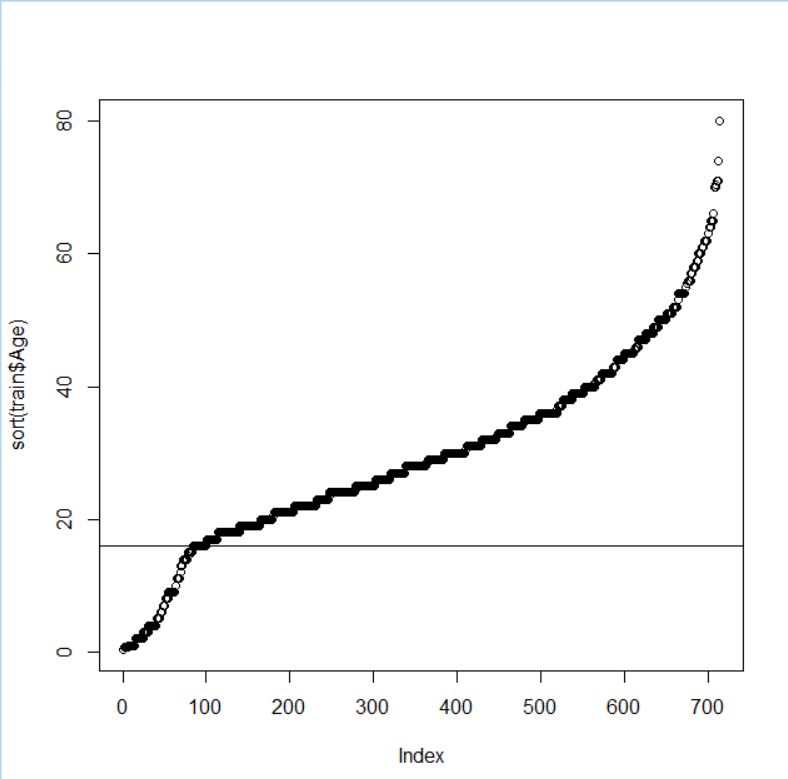
abline(h = 16) というコマンドを追加して、16歳 の水準に水平線を入れてみました。ちょうどこの年齢ぐらいから曲線の傾きが変わっています。そこで、年齢を16歳以下と16歳より上の2つのグループにわけました。数値データを factor にするには、cut関数を使います。
NA, 年齢が分からない乗客が 177人いたのですね。
SibSpを調べます。これは、兄弟姉妹、配偶者の人数です。

データ型は int(整数) です。ヒストグラム、カーネル密度グラフ、小さい順グラフの基本3グラフでデータの散らばり具合を見てみましょう。

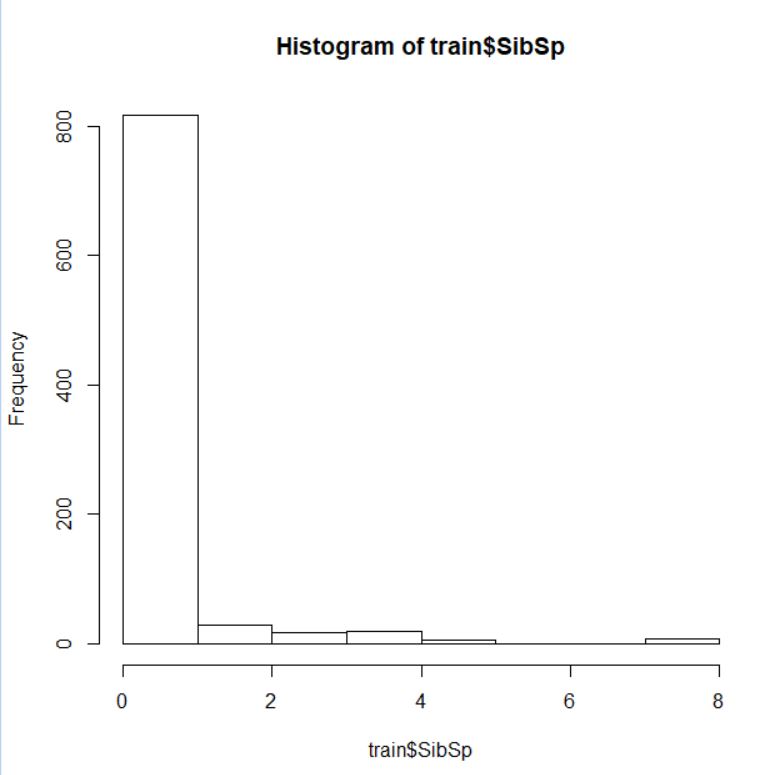
0 の人がほとんどのようです。

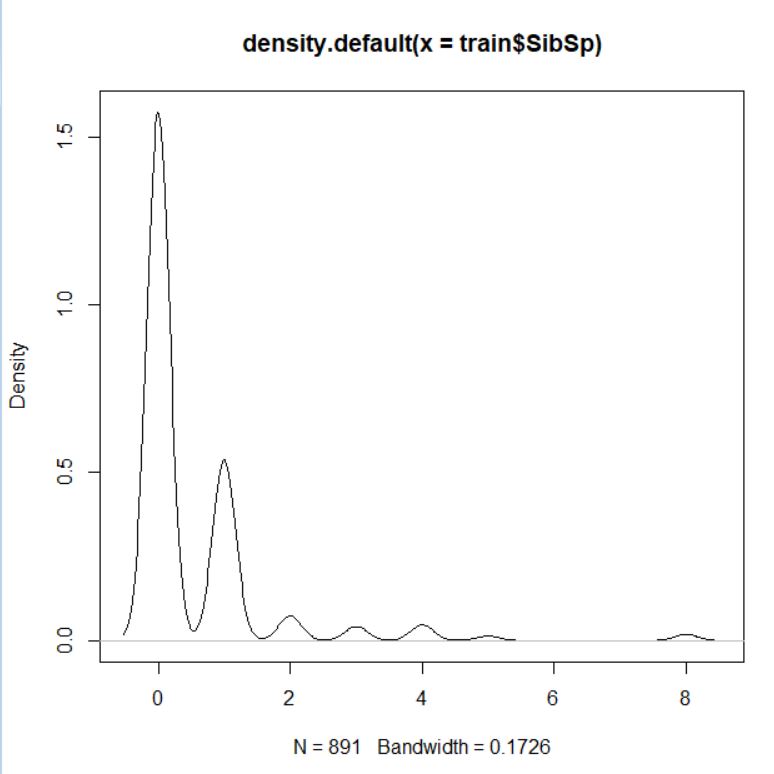

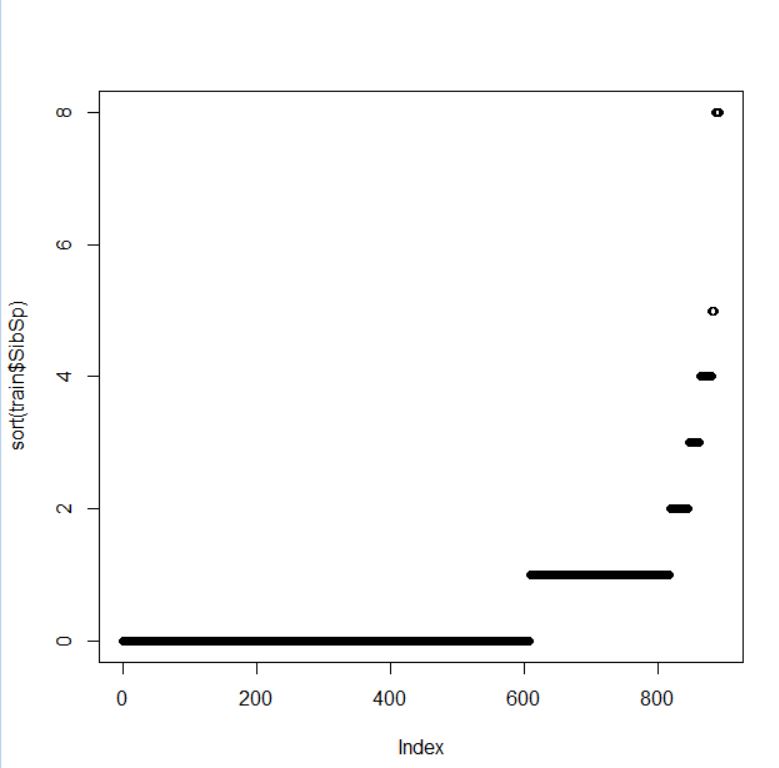
SibSp は大半が 0 だとわかりましたので、0 か 0 でないかの2つのファクターに変換します。
0 が 608人、0 でないのが 283人です。
Parchを調べましょう。これは子供、両親の人数です。

整数型ですね。基本3グラフでデータを視覚化します。

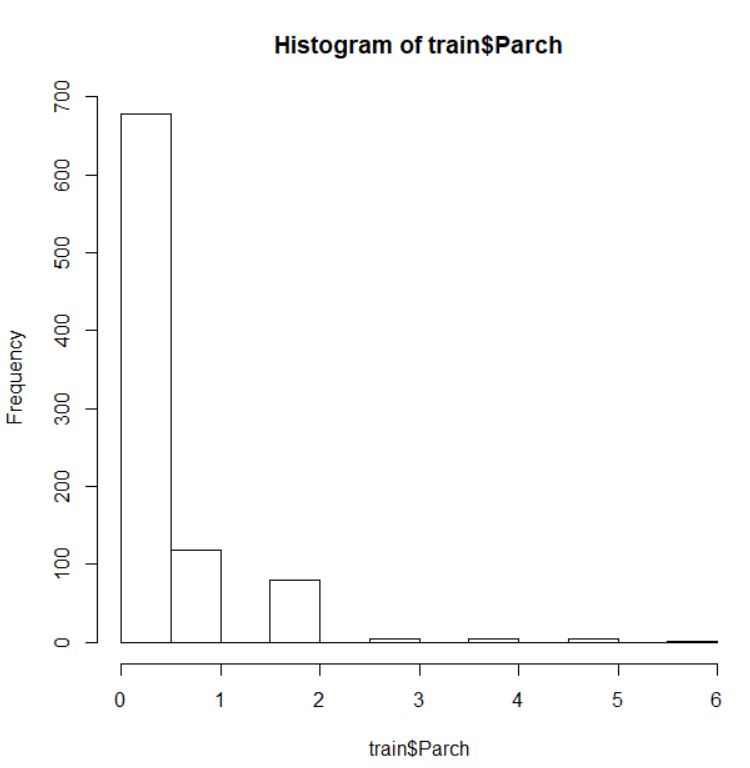

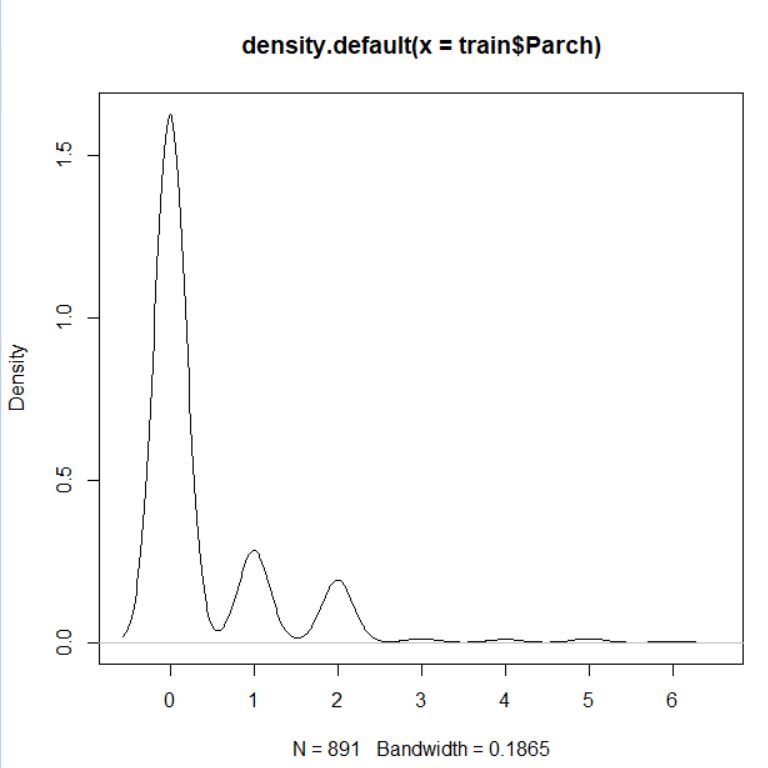

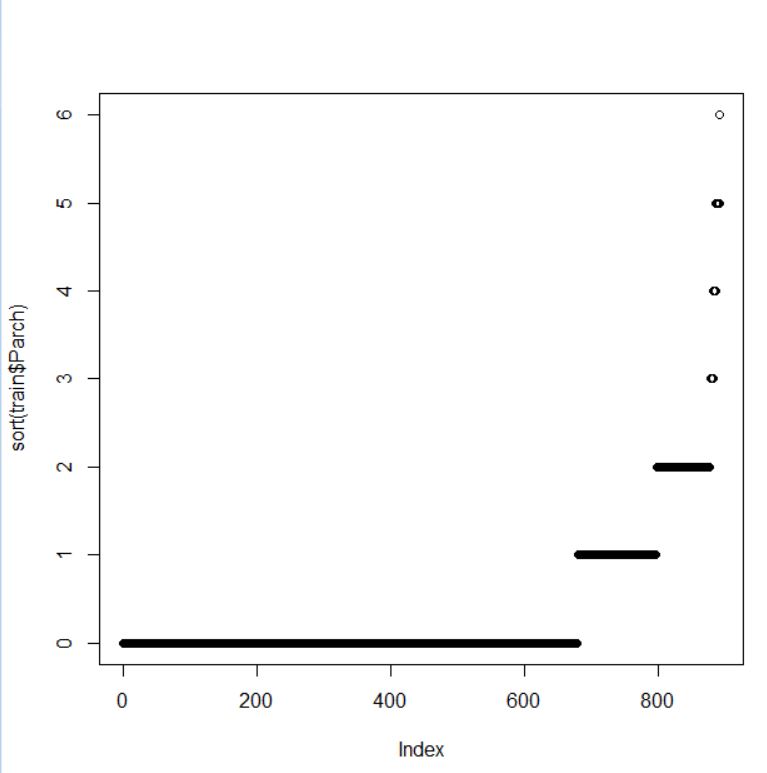
大半の人が 0 ですね。この Parch も 0 か 0 でないかの2つのファクターにします。
0 の人は 678人です。
Ticket を調べましょう。str関数でデータ型を確認します。
データ型は factor で、level が 681 もあります。これも分析には使わないことにします。
Fare, 料金はどうでしょうか?

データ型は number ですね。基本3グラフで視覚化します。

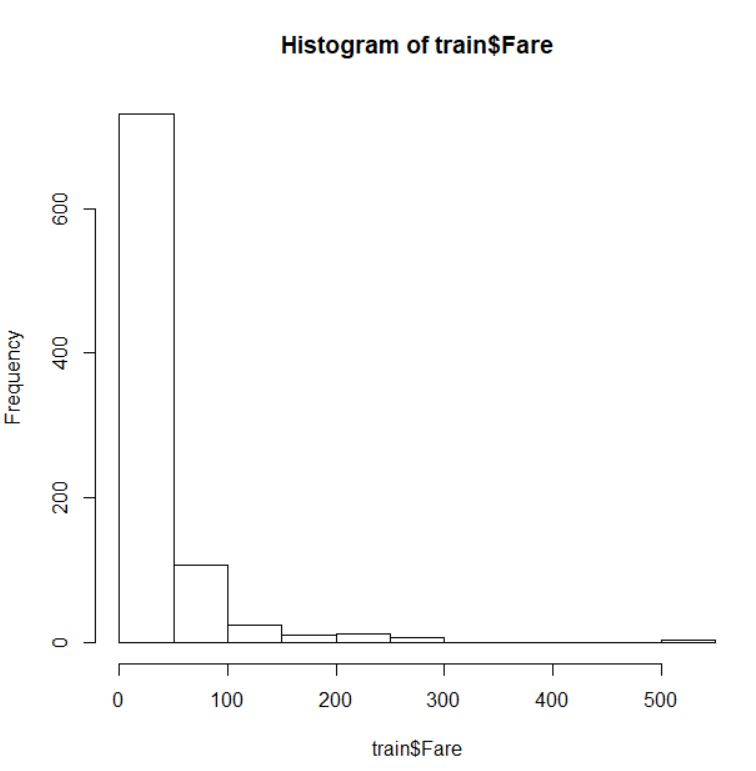

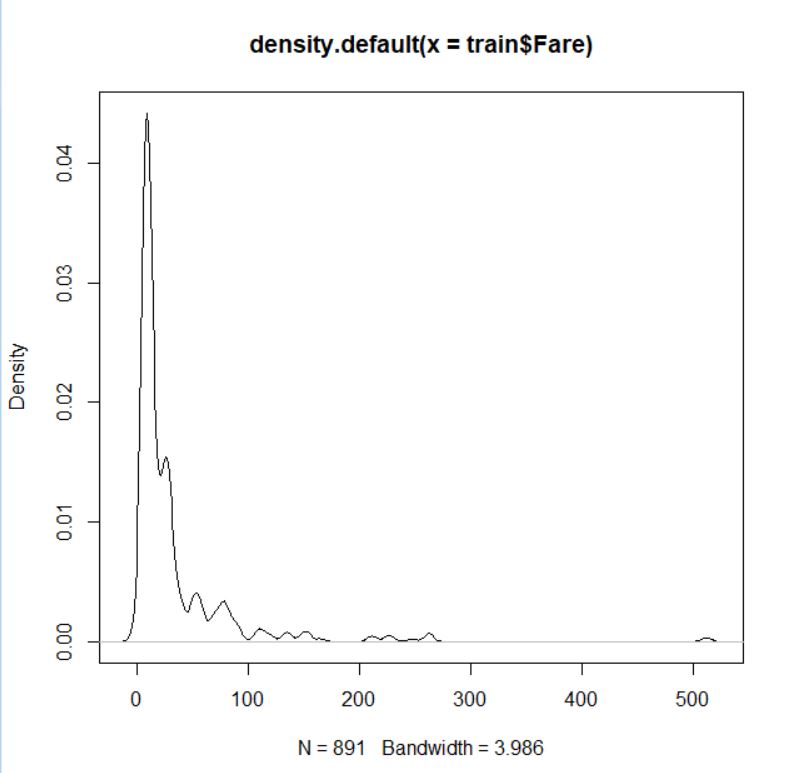

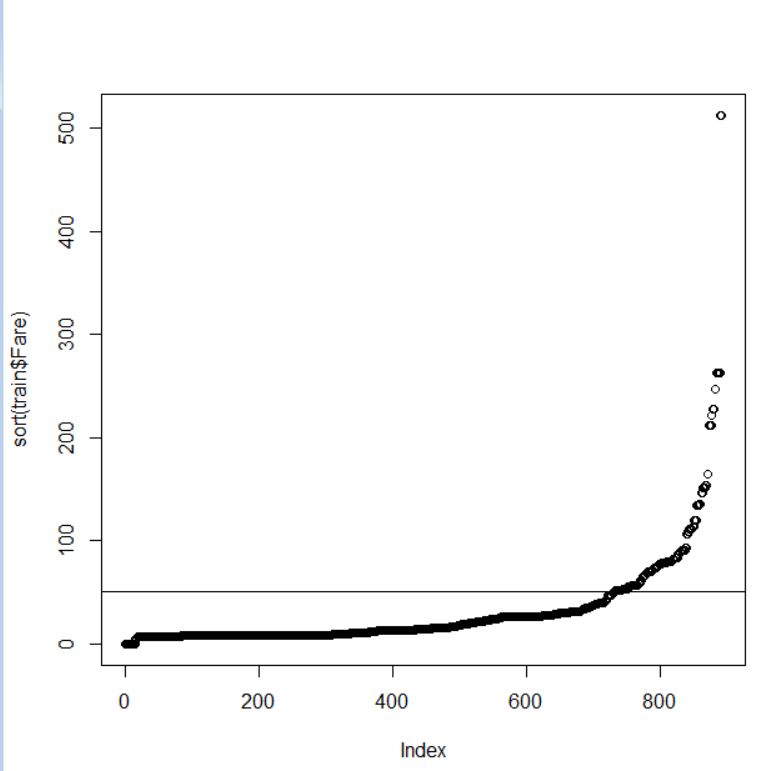
abline関数で 50 の水準に水平線を引きました。ほとんどが 50 以下の運賃だとわかります。なので、50以下、50より大きいの2つのファクターに変換します。
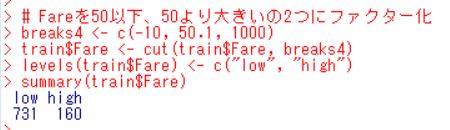
50より高い運賃の人は160人です。
Cabin はどんな感じでしょうか?
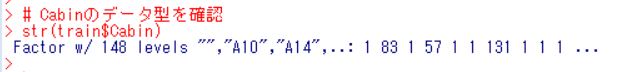
Cabin は factor で 148もレベルがあります。手に負えないので、分析には使わないことにします。
最後の変数は、Embarked です。寄港地という意味だと思います。

大半が S です。なので、S と S以外の2つのグループに二分します。

以上で各変数の様子がわかり、分析に使う変数は2つのファクターに変換しました。
次のステップは Survived と各変数のクロス表をカイ自乗検定し、関連性があれば、標準化残差を計算しましょう。
まずは、Pclass です。

p-value < 2.2e-16 < 0.05 なので、Pclass は Survived に関連しています。具体的には non-3 だと生存に有利です。3 は3等客ですから、1等客と2等客が生存確率が高いということです。。現実を感じます。3等客でない場合は、9.62点を付与しましょう。
次は、Sex です。

p-value < 2.2e-16 < 0.05 ですから、Sex は Survived と関連があります。femail, つまり女性のほうが生存しやすいです。女性には、16.2点を付与しましょう。
次は、Age です。

p-value < 0.0023 ですから、年齢も生死に関連あります。子供だと生存する確率が高いですね。子供、16歳以下には 3.16点を付与しましょう。
次は、SibSp, 兄弟姉妹・配偶者です。

p-value < 0.0007128 なので SibSp もSurvived と関連あります。0 でないほうが有利です。SibSp が 0 でない乗客に 3.46点を付与しましょう。
次は、Parch です。

p-value < 1.565e-05 ですから 0.05 より小さく、Parch は Survived と関連があります。non-zero のほうが生存に有利です。non-zero の乗客に 4.40点を付与しましょう。
SibSp, Parch ともに 0 でないと生存に有利でした。家族と一緒に乗ってた乗客のほうが生存に有利だったということですね。家族で助け合って避難したのでしょうね。
次は、Fare です。

p-value < 2.2e-16 ですので Fare と Survived は関連があり、運賃が高いほうが生存率が高くなります。運賃が高い乗客は、1等、2等の乗客でしょうからね。50ドル以上の運賃の乗客に 8.54点を付与することにします。
最後は Embarked です。

p-value = 4.89e-06 ですから Embarked と Survived は関連がありました。S でないと生存に有利でした。S でない乗客に 4.65点を付与することにしましょう。
まとめると、
Pclass は non-3 が 9.62点
Sex は female が 16.2点
Age は child(16歳以下)が 3.16点
SibSp は non-zero が 3.46点
Parch は non-zero が 4.40点
Fare は high が 8.54点
Embarked は non-S が 4.65点
という加点方法です。この加点方法に基づいて各乗客に点数を付与して、総合得点、Score を計算してみます。
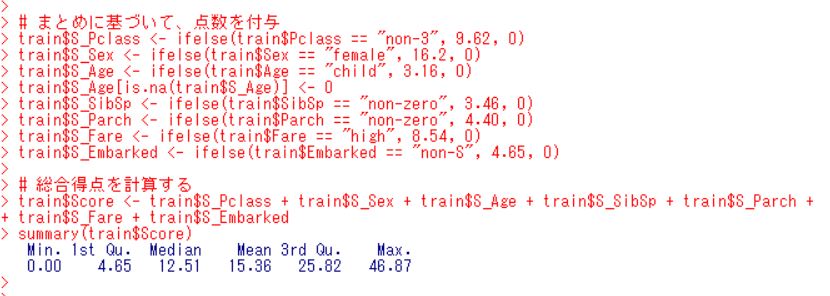
総合得点、 Score は最小が 0.00, 最大が 46.87, 中央値が 12.51, 平均値が 15.36 です。基本3グラフで Score のバラツキ具合を視覚化しましょう。

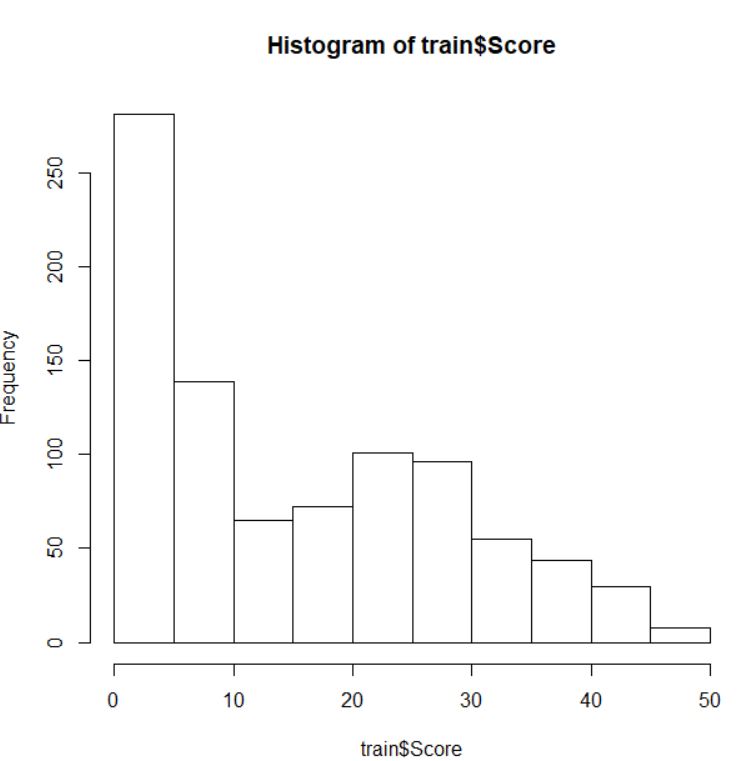

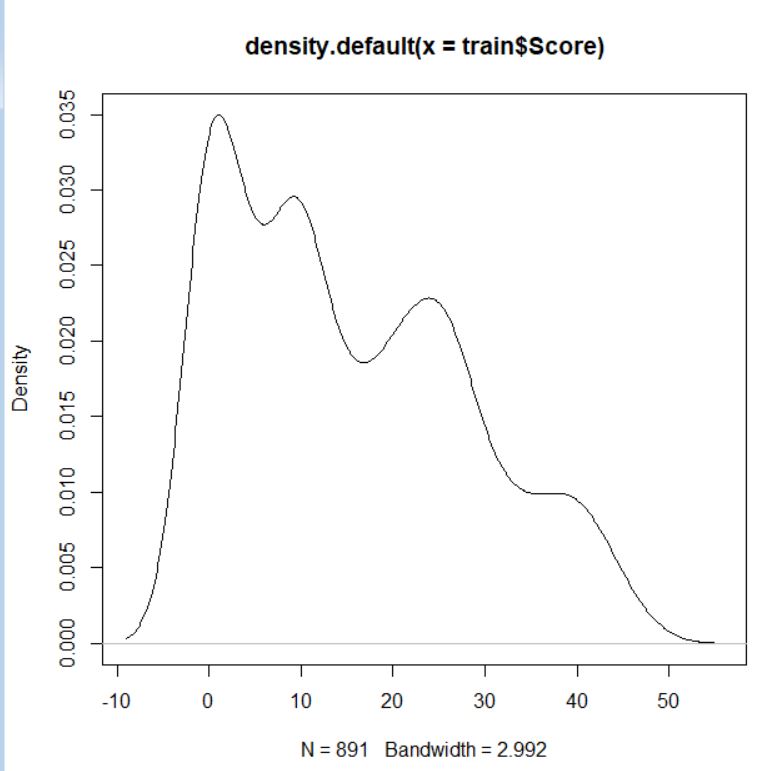

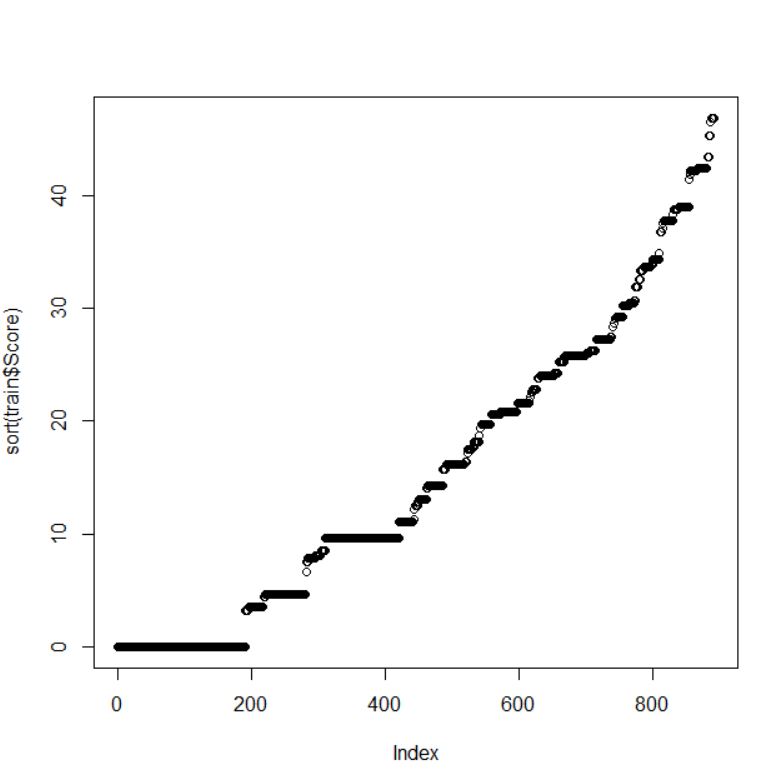
Survived と Score の関係を plot関数で視覚化しましょう。

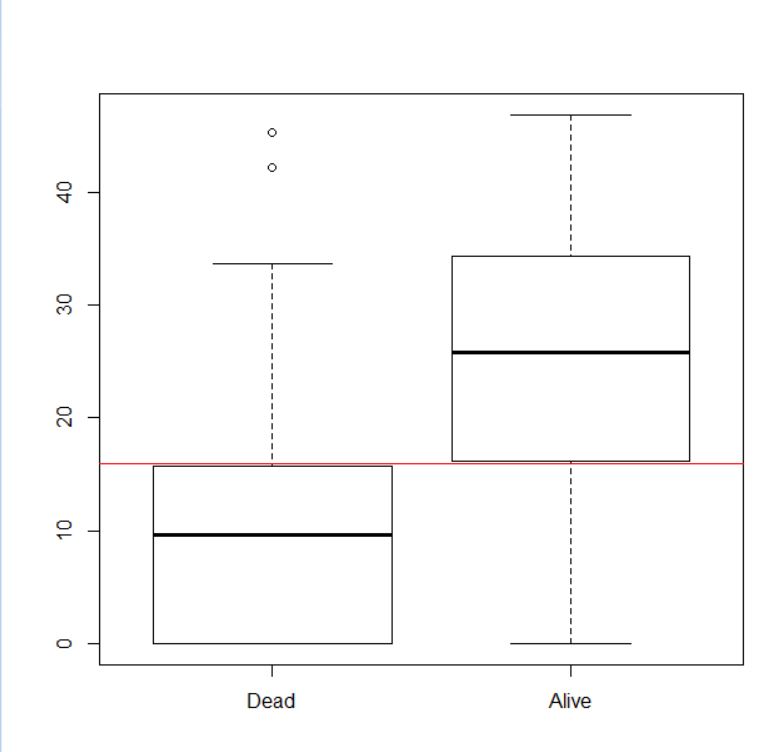
Dead と Alive で箱ひげ図が描かれます。15.9点ぐらいで Dead の第3分位、Alive の第1分位が分かれるようなので、15.9以下なら死亡、それより高い点数ならば生存を判断しました。
こうして Score を test.csv ファイルのデータを使って計算して Kaggle に submit します。結果は、、
Score が 0.71770 ということで、正解率が 71.77% だったということです。
これは、

10100 / 10858 ということですので、全然ダメですね。。。
Age や Fare などの連続数値を強引に2つのグループにしたり、SibSp, Parch, Embarked など 2つ以上の値をとるものも2つのグループにしたり、変数どうしの相互作用を考慮していなかったりなどと改善の余地はまだまだ多くあります。
ランダムフォレストやその他の手法をマスターしたら、再度チャレンジしたいと思います。
今回の分析を通じて、女性や子ども、1等客、2等客、家族がいる者などの生存率が高いことがわかりました。そして、映画、タイタニックをまたみようかな、と思いました。
次回は
です。
![タイタニック(2枚組) [AmazonDVDコレクション] タイタニック(2枚組) [AmazonDVDコレクション]](https://images-fe.ssl-images-amazon.com/images/I/51zZPJ6MbfL._SL160_.jpg)