今回は、OECDのデータを分析してみようと思います。
ここからいろいろデータを取得できるようです。
今回は2017年と2018年のIndustrial Production, 鉱工業生産の伸び率を分析してみます。
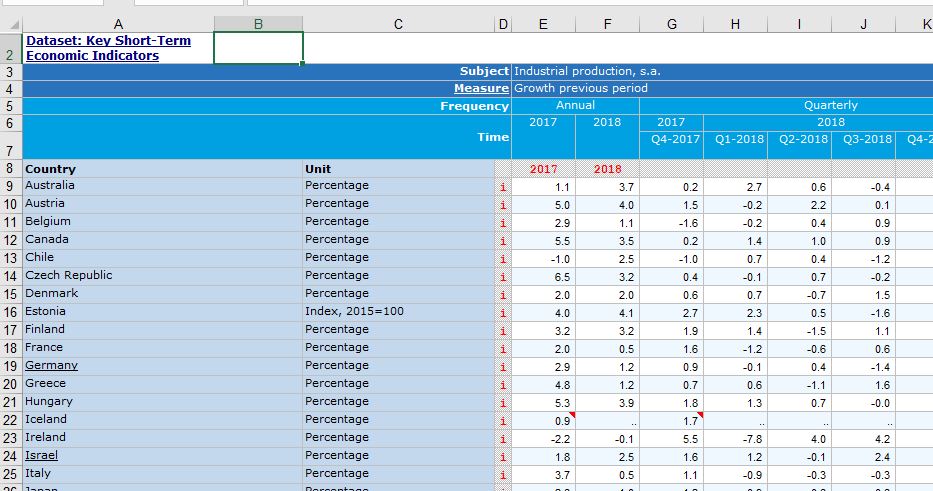
Excelにデータをダウンロードしたらこんな感じでした。E8に2017, F8のセルに2018と入力しました。このファイルをR言語のread.csv関数で読み込んで分析しようと思います。

str関数でどんな風に読み込まれたか確認してみます。
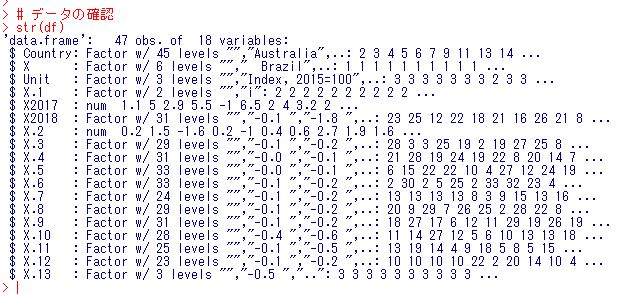
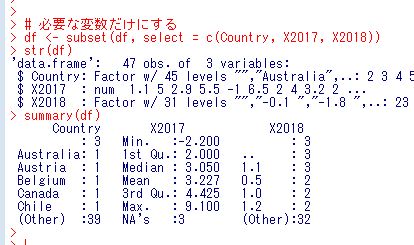
うまく読み込んだようです。必要な変数は、Country, X2017, X2018の三つです。subset関数でこの変数だけにしてしまいましょう。
X2017にNAがあるのでNAの行をna.omit関数で削除してしまいます。
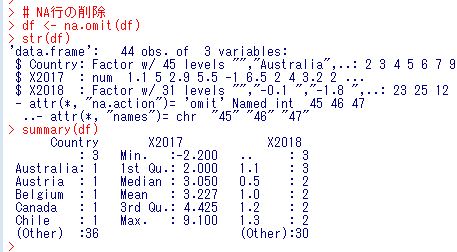
X2018が数値データではなくて、ファクタデータになっています。
どんなデータがあるか確認してみます。

空白のものと、.. というものがあるために数値データでなくファクタになってしまっていますね。空白のデータの行を削除します。subset関数です。

空白、.. のデータが0になりました。これを数値データにするには、まず文字列に変換します。as.character関数です。そしてas.numeric関数で数値にします。

X2018が数値データになりました。よく見るとCountryに空白のファクタ水準があります。これを削除します。as.character関数で文字列にしてから、as.factor関数でファクタに戻します。

これでやっとデータが整いました。
2017年のIP(Industrial Production, 鉱工業生産)の平均値は3.332%成長で、2018年は2.105%成長です。この違いは有意な違いなのでしょうか?
まずは、2017年の分散と2018年の分散を比較します。
var.test関数を使います。

p-value = 0.05845 で0.05よりも大きいので分散に違いがあるとは言えないです。
それでは平均値に違いがあるかどうか、t.test関数でみてみましょう。X2017とX2018は同じ国の2017年、2018年のデータがあるので、対になっているデータですね。

p-value = 0.002391 と0.05よりも小さいので、2017年の平均値3.332%と2018年の平均値2.105%は有意な違いがあるということです。
paired = Fとして対のデータとしないで検定してみましょう。

この場合でもp-value = 0.01045と0.05よりも小さいので二つの平均値は明らかに違いがあるとわかります。
視覚的にも違いを見てみましょう。hist関数でヒストグラムを書いてみます。

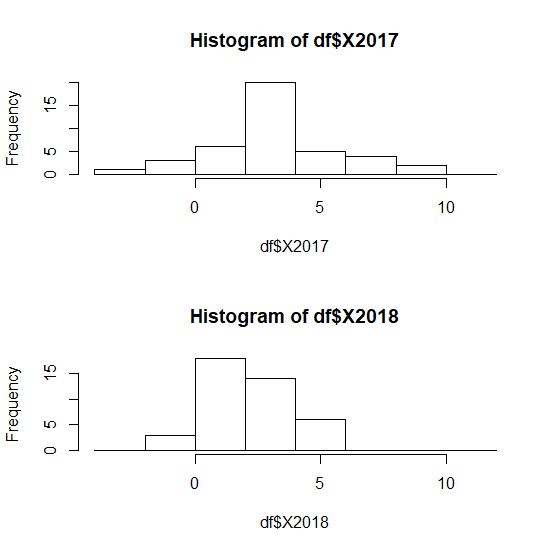
あきらかに下のヒストグラム、2018年のほうが分布が左によっています。
2017年と2018年の散布図をplot関数で描いてみます。

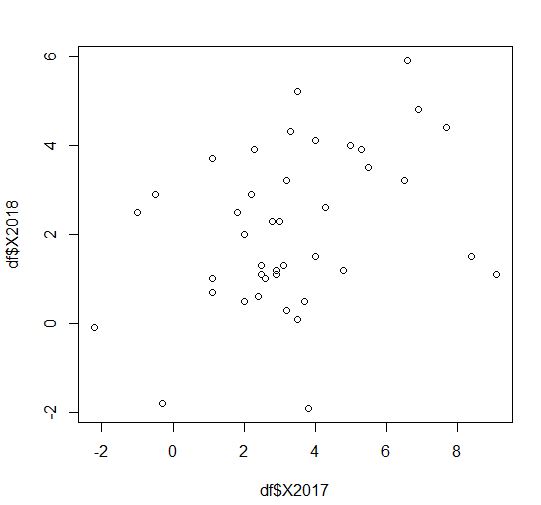
正の相関があるような気がします。cor.test関数で確認します。

相関係数は0.359でp-valueは0.02111です。p値が0.05より小さいですから、正の相関があるとわかります。
2017年の伸び率の上位の国、下位の国を見てみましょう。order関数を使います。
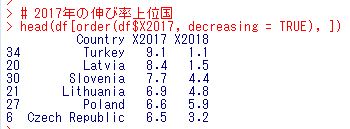
トルコが9.1%成長で一番です。下位の国はどこでしょうか?
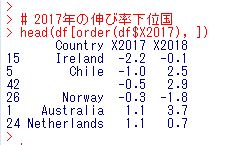
アイルランドが-.2.2%成長で一番低かったです。
2018年の伸び率上位の国はどこでしょうか?
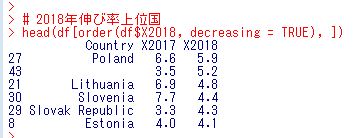
ポーランドが5.9%成長で一番です。あれ?名前が空白の行が残っていましたね。おかしいな。。
最後に2018年の伸び率下位の国はどこでしょうか?
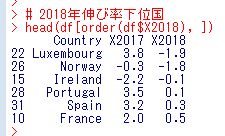
ルクセンブルグが-1.9%成長で一番低いです。
今回は以上です。
R言語のコードは以下のとおりです。
# CSVファイルの読み込み
df <- read.csv("oecd_ip.csv", skip = 7)
# データの確認
str(df)
# 必要な変数だけにする
df <- subset(df, select = c(Country, X2017, X2018))
str(df)
summary(df)
# NA行の削除
df <- na.omit(df)
str(df)
summary(df)
# X2018のデータの確認
table(df$X2018)
# X2018の空白行を削除
df <- subset(df, subset = (X2018 != "") )
df <- subset(df, subset = (X2018 != ".."))
table(df$X2018)
# X2018を文字列に変換
df$X2018 <- as.character(df$X2018)
# X2018を数値に変換
df$X2018 <- as.numeric(df$X2018)
# 確認
str(df)
summary(df)
# Countryの空白のファクタ水準を削除
df$Country <- as.character(df$Country)
df$Country <- as.factor(df$Country)
str(df)
summary(df)
# 分散に違いがあるかどうか
var.test(df$X2017, df$X2018)
# 平均値に違いがあるかどうか
t.test(df$X2017, df$X2018, paired = T)
# 対のデータとみなさいで検証
t.test(df$X2017, df$X2018, paired = F)
# ヒストグラムの作成
par(mfrow = c(2, 1))
hist(df$X2017, breaks = seq(-4,12, 2))
hist(df$X2018, breaks = seq(-4,12, 2))
par(mfrow = c(1, 1))
# 散布図
plot(df$X2017, df$X2018)
# 相関の検定
cor.test(df$X2017, df$X2018)
# 2017年の伸び率上位国
head(df[order(df$X2017, decreasing = TRUE), ])
# 2017年の伸び率下位国
head(df[order(df$X2017), ])
# 2018年伸び率上位国
head(df[order(df$X2018, decreasing = TRUE), ])
# 2018年伸び率下位国
head(df[order(df$X2018), ])