の続きです。
今回は、普通にlm関数を使って回帰分析をしてみます。
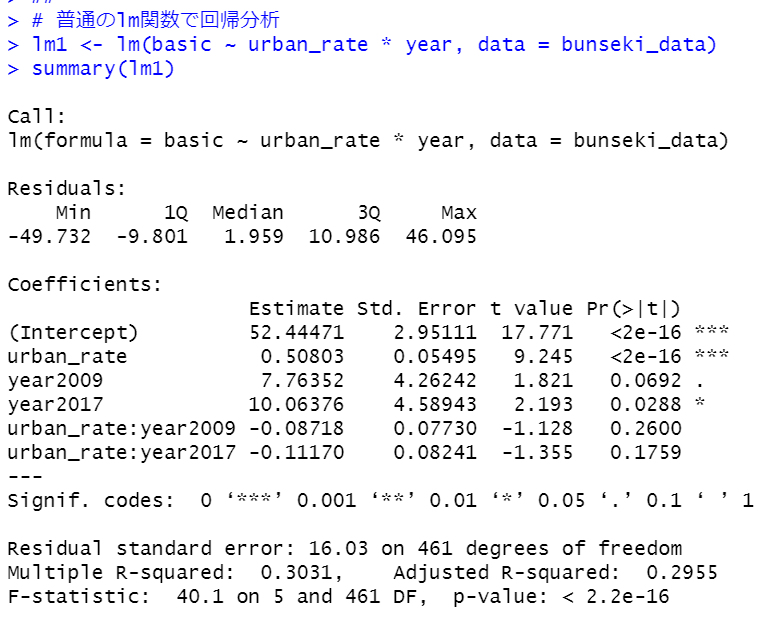
p-value < 2.23-16と0.05よりも小さいので有意なモデルです。urban_rate:year2009とurban_rate:year2017は必要ないようです。update関数で削除します。

update関数で、urban_rate:yearの交互作用の項を削除して、anova関数でlm1とlm2を比較しています。Pr(>F)が0.3437と0.05よりも大きいので、lm1とlm2では有意な違いはありません。なので、より単純なモデルのlm2を採用します。
summary関数でlm2を見てみます。
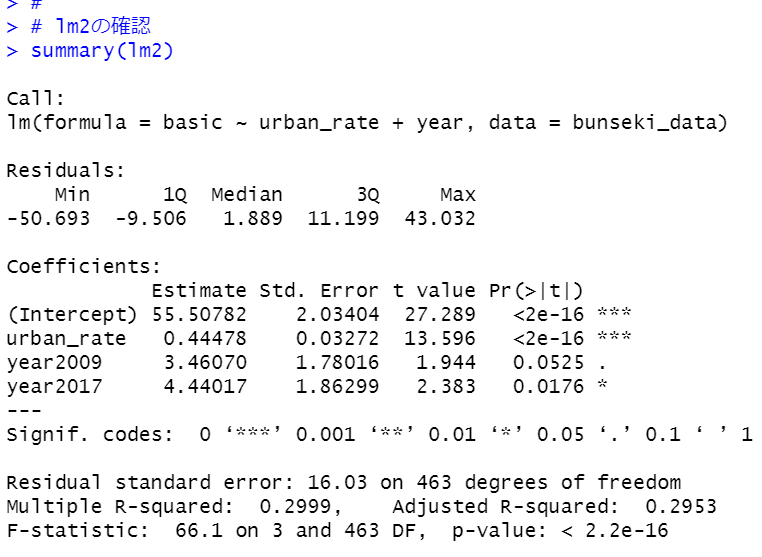
year2009の係数は3.46070で、標準誤差が1.78016ですのでyear2009の信頼区間は、3.46070-1.78016=1.68054 から3.46070+1.78016=5.24086の間です。これはyear2017の係数の4.44017とかぶります。つまり、year2009とyear2017は有意な差が無いということですね。
なので、yearを2000と2000以外の2つのファクターに分けて回帰分析モデルを作ります。

こうしてyear2という変数を作りました。これは2000と2009+17という2つのファクターを持つ変数です。
このyear2を説明変数にして回帰分析モデルを作ります。
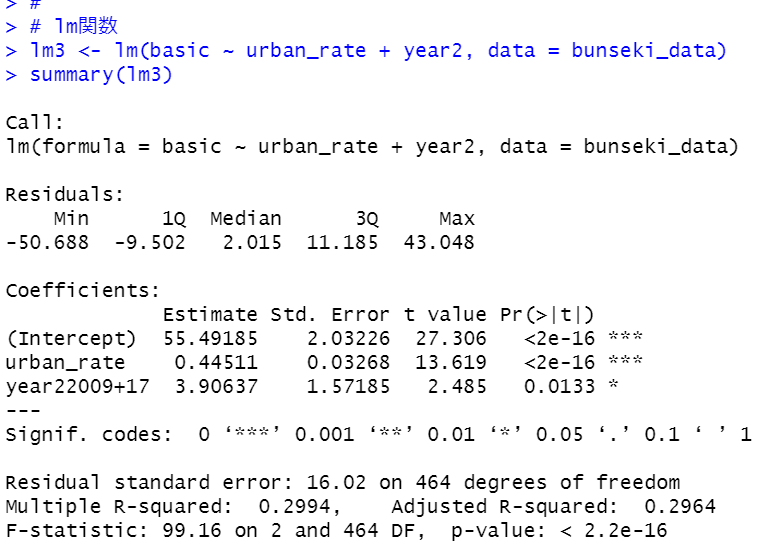
p-value < 2.23-16と0.05なので有意なモデルです。year2の2009+17のp値も0.0133と0.05よりも小さいので有意です。
anova関数でlm2とlm3を比較してみましょう。

p値は0.593なので、lm2とlm3では有意な違いはありません。なので、単純なlm3のほうを採用します。
lm3の残差プロットなどを描いてみます。

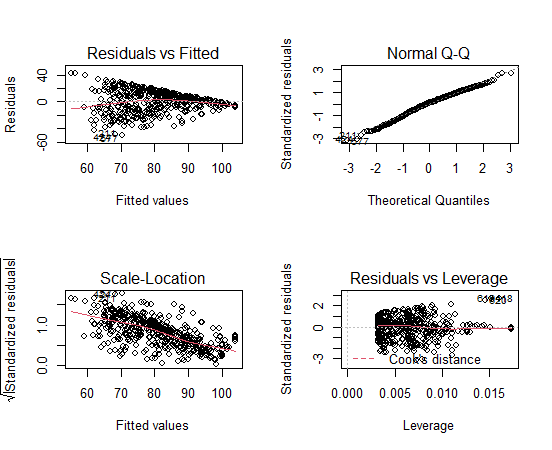
左上の散布図が残差プロットです。Fitted valuesが大きくなるほど、Residualsがちいさくなるという明確なパターンが発生しています。
つまり、線形回帰分析モデルでは問題がある、ということですね。
今回は以上です。