に引き続き、就業構造基本調査のデータ分析をしていきます。
前回までで「仕事者率」「家事者率」「通学者率」という変数を計算し、男性のほうが女性よりも「仕事者率」が高いことがわかりました。
今回は、「仕事者率」を被説明変数にして、「男女」「続柄など」「年齢」の3つを説明変数にするモデルを作成してみたいと思います。できるかな?
いまいちど、data2の確認をします。

「男女」については、「性別」というダミー変数(男=1, 女=0)を設定します。
「続柄など」についてはそれぞれの属性のダミー変数を設定します。例えば、単身(うち単身者=1, その他は0)などです。
「年齢」についても同様にダミー変数を設定します。
まずは「性別」というダミー変数をifelse関数を使って作成します。

このようにできました。まずはこの「性別」だけで仕事者率を表すモデルを作成してみましょう。
モデル式は、仕事者率 = a + b x 性別 + 誤差項
となるのかな?ちょっと自信ないですが。lm関数でモデル式を推測できます。

うまくできました。推測されたモデル式は、仕事者率 = 0.4177 + 0.1635 x 性別 + 誤差項
ですね。0.4177 が女性の仕事者率の平均で、それに0.1635上乗せすると男性の仕事者率の平均になります。
anova関数でANOVA表を表示しています。
「続柄など」のダミー変数を作りましょう。全部の属性についてダミー変数を作るのは面倒なので、世帯主なら1、そうでないなら0というダミー変数を作りましょう。

このようにifelse関数で作成しました。それではこの「世帯主」というダミー変数も加えたモデル式を推測してみましょう。
仕事者率 = a + b1 x 性別 + b2 x 世帯主 + 誤差項
という式です。lm関数で実行します。

推測されたモデル式は、
仕事者率 = 0.41131 + 0.16346 x 性別 + 0.05067 x 世帯主 + 誤差項
です。世帯主だと仕事者率が0.05067だけアップします。
「年齢」もダミー変数を作りましょう。普通に働く年齢の20歳から64歳までを「働年代」としてみましょう。

ifelse関数で複数条件をorでつなぐときは、| を使います。
それではこの「働年代」も加えたモデル式を推測してみましょう。
仕事者率 = a + b1 x 性別 + b2 x 世帯主 + b3 x 働年代 + 誤差項
という式です。lm関数です。
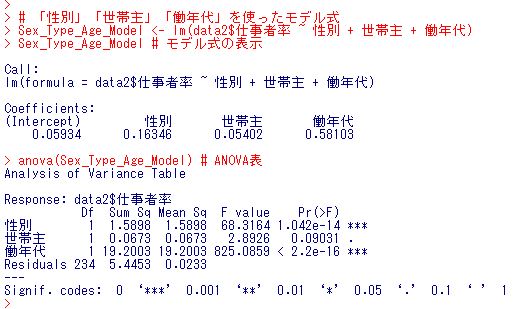
推測されたモデル式は、
仕事者率 = 0.05934 + 0.16346 x 性別 + 0.05402 x 世帯主 + 0.581103 x 働年代 + 誤差項
です。
働く年代かどうかが一番影響していることがわかりました。
それぞれのモデルをsummary関数で処理して決定係数やF統計量をみてみましょう。

一番下の行、F-statisticのp-value が0.0001272 < 0.05なのでこのモデルは有効です。調整決定係数(Adjusted R-squared)は0.05646でした。

p-value = 0.0004779 < 0.05 なので、このモデルは有効です。調整済み決定係数は0.05503でした。

p-value < 2.2e-16 < 0.05ですから、このモデルも有効です。調整済み決定係数が0.7903と3つのモデルの中では一番高いです。
今回は以上です。