の続きです。今回もANOVAをします。今度は、Sector(製造業、非製造業、全産業)を説明変数にして、Value、短観の値を反応変数にします。
またグラフでSectorによって短観の値に違いがあるか見てみましょう。

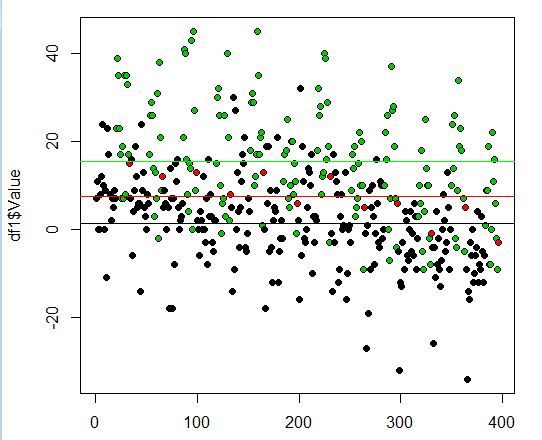
黒い点が製造業で黒い水平線が製造業の短観の平均値です。
赤い点が全産業で赤い水平線が全産業の短観の平均値です。
緑の点が非製造業で緑の水平線が非製造業の平均値です。業種による違いは大きそうですね。
tapply関数でそれぞれの業種の平均値を調べましょう。

製造業の平均が1.39, 全産業の平均が7.57, 非製造業の平均が15.4です。業種による違いはありそうですね。
SSY, sum of the squares of the differences between y values and the overall meanを計算します。
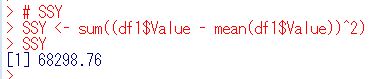
SSYは68298です。
SSE, the error sum of squaresを計算します。

SSEは50073です。
SSAはSSY - SSEです。

ここまでの結果をもとに、ANOVA表を作成します。
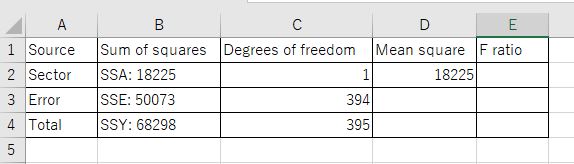
D3のセル、ErrorのMean squareを計算します。


E2のセル、F ratioを計算します。

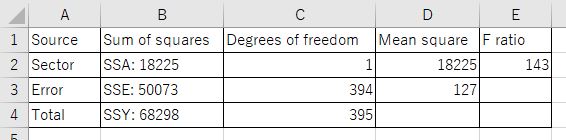
このF ratioの143が意味のある大きさかどうかが問題です。qf関数で調べます。

143は3.865よりも大きいので、Sectorによって短観の結果に違いがある、ということですね。
aov関数とsummary関数で確認します。

あ!Sectorは製造業、全産業、非製造業でしたから、Degrees of freedomは1ではなくて2ですね。さっきのANOVA表を訂正します。
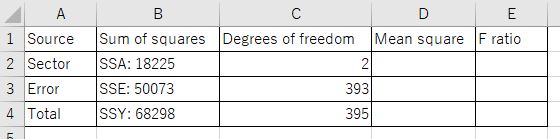
Mean square, F ratioを計算しなおします。

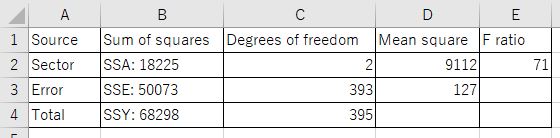
あらためて、aov関数とsummary関数の結果を提示します。

p値が2e-16よりも小さいので、Sectorによって短観の値に違いはあります。
製造業よりも非製造業のほうが景況感はいいようですね。
今回は以上です。