の続きです。
前回は2006年度よりも2014年度のほうが死亡者が多かったことがわかりました。
今回は2015年度のデータで、総人口1万人当りの死亡者数と人口密度、県内総生産の関係を見てみます。
まずは、2015年度だけのデータフレームを作成します。d15という名前のデータフレームにしました。
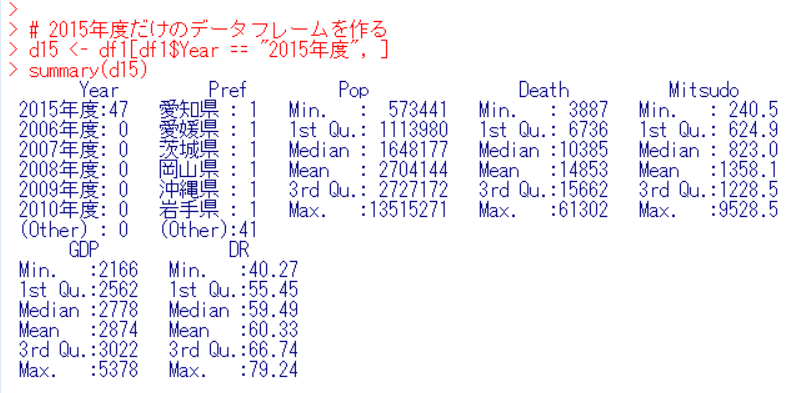
Yearは必要ないので、削除します。

Mitsudo(人口密度), GDP(一人当り県内総生産), DR(1万人当たり死亡者数)の分布の形態をヒストグラムで見てみます。hist関数です。


人口密度や一人当り県内総生産は右に裾野が広がっていますね。1万人当りの死亡者数は、左右対称っぽいです。
散布図を見てみましょう


青枠で囲った2つの散布図が縦軸がDR(死亡者数)です。左の散布図が横軸が人口密度、右の散布図が横軸がGDPですね。
人口密度も一人当り県内総生産も右の裾野が長い分布ですので、対数をとって散布図を描いてみます。


どちらも右肩下がりの散布図ですね。
cor関数で相関関係を調べてみます。

死亡者数と人口密度の相関係数は、-0.569。
死亡者数と人口密度の対数の相関係数は、-0.761。
死亡者数と県内総生産の相関係数は、-0.438。
死亡者数と県内総生産の対数の相関係数は、-0.438。
人口密度と県内総生産の相関係数は、0.645。
人口密度の対数と県内総生産の対数の相関係数は、0.525。
対数をとった値のほうが死亡者数との相関が高く、かつお互いの相関係数は低いです。
なので、対数をとった値を説明変数にして、重回帰分析をしてみます。

log(GDP)の係数のp値が0.64164と0.05よちも大きいです。log(GDP)はいらないのですね。削除しましょう。

p値は0.6416と0.05よりも大きいので、model1とmodel2で有意な違いはありません。
単純なほうのmodel2を採用します。

model2のp値は5.478e-10と0.05よりも小さいので有意なモデルです。
人口1万人当りの生活習慣病による死者数 = 120.615 - 8.819 x 人口密度の対数値
というモデル式です。1人当りの県内総生産額は、人口密度を考慮すると必要ない変数だとわかりました。
散布図(横軸が人口密度の対数値、縦軸が死亡者数)にモデルの回帰直線を重ねてみます。


直線よりも曲線のほうがうまく回帰できそうですね。2乗項を加えてみます。

anova関数でmodel2とmodel3を比較すると、p値は0.03159と0.05よりも小さくなりました。model2とmodel3では有意な違いがあるのですね。AIC関数でどちらのモデルがいいか見てみましょう。

model3のほうがAICの値が小さいので、良いモデルですね。みてみましょう。

model3のp値は5.327e-10で0.05よりも小さいので、有意なモデルです。
切片、log(Mitsudo)の係数, log(Mitsudo)^2の係数それぞれのp値も0.05以下ですね。
model3は
人口1万人当りの生活習慣病の死亡者数 = 233.6892 - 40.3289 x Mitsudoの対数値 + 2.1635 x Mitsudoの対数値の2乗
です。
先ほどと同じように散布図に回帰曲線を重ねてみましょう。
まず、log(Mitsudo)の範囲に合わせてxの値を作成します。

seq関数でスタートがmin(log(d15$Mitsudo)), 終了がmax(log(d15$Mitsudo))で個数が100個の数値ベクトルを作りました。

次に上のようにmodel3の式を当てはめてyの値を作成しました。
さあ、散布図にmodel2の回帰直線、model3の回帰曲線をかさねます。


青い曲線(model3)のほうが緑の散布図にフィットしているように見えます。
今回は以上です。