の続きです。
今回はR言語のlm関数で重回帰分析をしてみたいと思います。
まず、対数変換後のavgPr(15-64歳人口割合の9年間の平均)、avgSh(1人当り県民所得の9年間の平均)、avgEn(1人当り最終エネルギー消費量)のヒストグラムをhist関数で描いてみます。

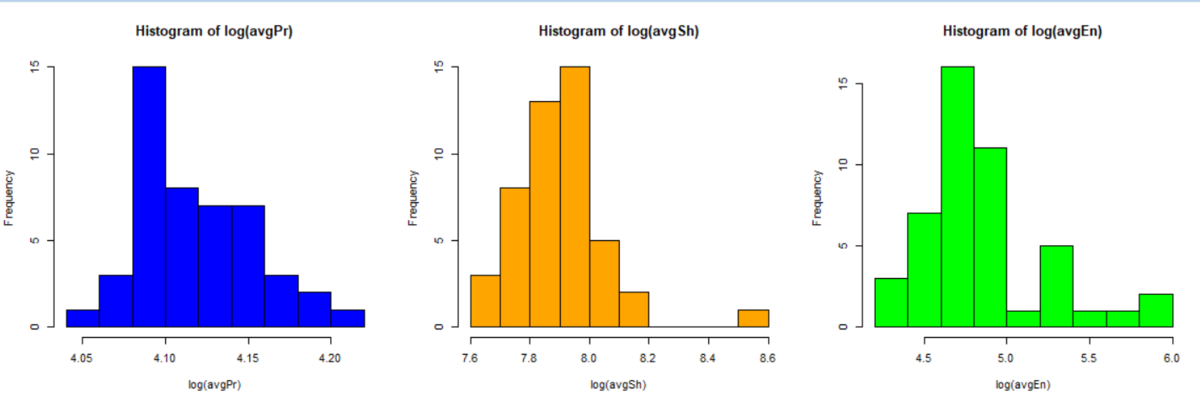
log(avgEn)がresponse variable(反応変数)で、log(avgPr)とlog(avgSh)explanatory variables(説明変数)です。
それぞれログをとった変数をlogdfという名前のデータフレームに格納してしまいます。

データフレームは、data.frame関数で作成できます。
それでは、lm関数で重回帰分析をしてみます。

一番下の行にあるp-valueは0.04276と0.05よりも小さいですから有意なモデルです。でも、各説明変数の係数のp値は0.05以上ですね。
とりあえず、p値が一番大きいPrを外したモデルを考えてみます。

p値は0.7082と0.05よりも大きいので、model1とmodel2に有意な違いは無いことがわかりました。model2を見てみましょう。

p値は0.02001とmodel1よりも小さいですね。すべての説明変数の係数のp値も0.05以下なので有意です。でも、R-squaredが0.2024なので、説明力は低いですね。
I(Pr^2)とShの交互作用を加えてみます。

p値は0.7273なので0.05よりも大きいので、加えても意味なかったですね。それでは、I(Pr^2):I(Sh^2)を加えてみます。

これも意味なかったですね。
それでは、Sh:I(Sh^2), つまりI(Sh^3)を加えてみます。

これも意味なかったですね。model2がいいということですね。
せっかくなので、3次元散布図を描いてみます。
stats.biopapyrus.jpのサイトを参考にしました。ありがとうございます。
まず、scatterplot3dというパッケージをインストールする必要があるそうです。

library関数でこのパッケージを読込みます。

あとは、scatterplot3d関数で3次元散布図が出来上がります。
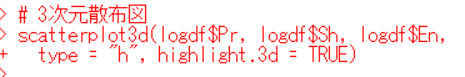
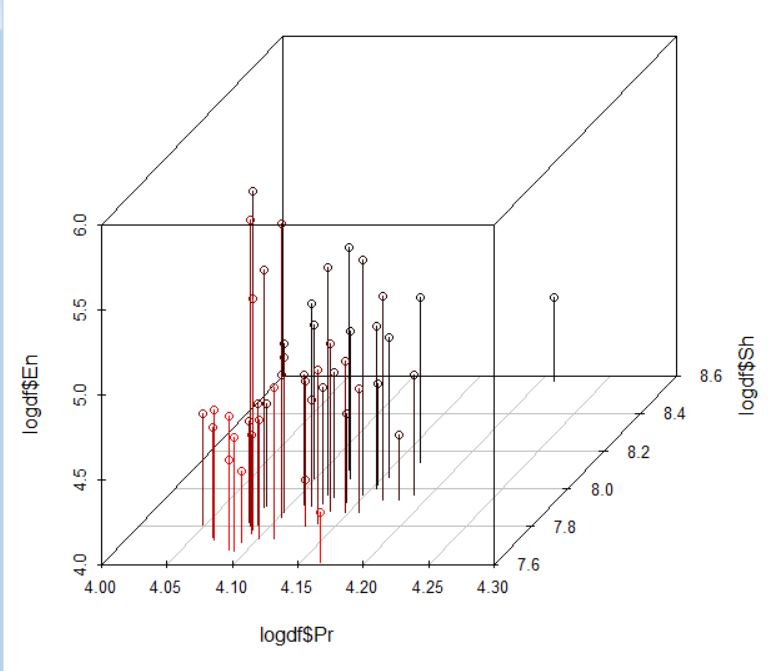
Z軸をEnではなくて、モデルで予測した値にしましょう。model2$fitted.valuesにすればいいです。
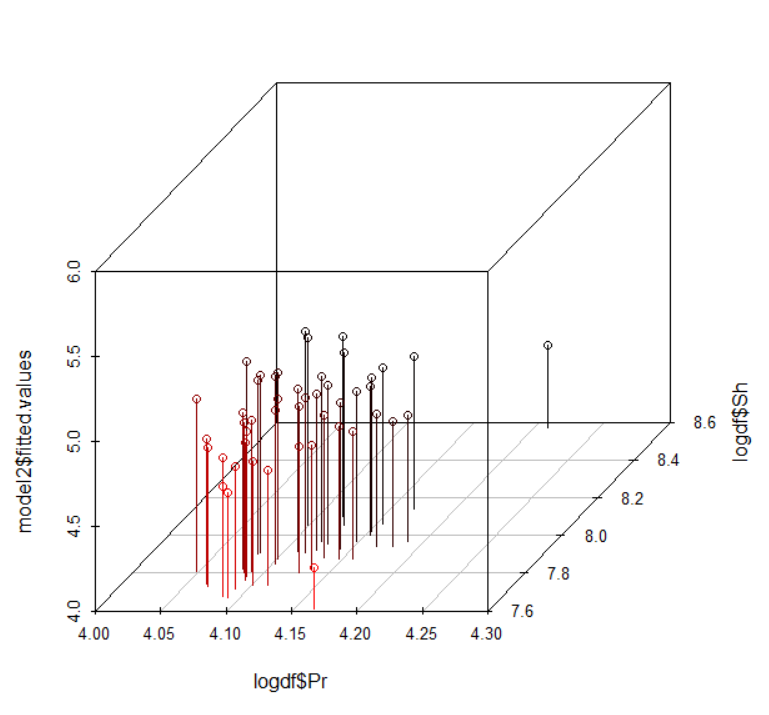
どうでしょうか?モデルの予測値のほうが実際の値よりもバラツキが小さいようですね。
最後にmodel2の残差プロットを見てみます。
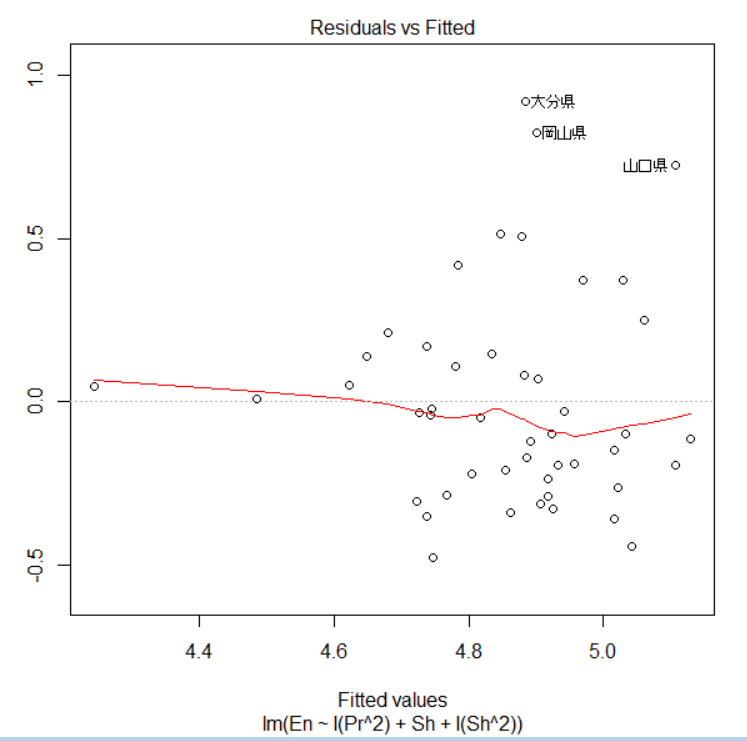
大分県、岡山県、山口県は前回の分析でもそうでしたがこの残差プロットでも外れていますね。
今回は以上です。