の続きです。
今回はR言語で回帰分析をします。老人福祉費または児童福祉を人口、面積、県内総生産の3つの変数で回帰分析します。事前の予想は、人口と県内総生産は関係あるけど、面積は関係ないんでは?と思います。
早速やってみます。lm関数を使います。

まずは、各変数の交差項と2乗した項目を加えたmaximum modelからスタートします。
p-value は2.2e-16より小さいので有意なモデルです。Adjusted R-squaredは0.9858ですのであてはまりもいいですね。avgPop:avgArea:avgGDPの3変数の交差項はp値が0.05よりも大きいので削除します。
update関数を使います。

anova関数でmodel1とmodel2を比較すると、p値が0.07087と0.05よりも大きいので、model1とmodel2では有意な違いはありません。従って、より単純なmodel2を採用します。model2をsummary関数で見てみます。

I(avgArea^2)はp値が0.334315なので削除しましょう。

p値が0.3343なので、model2とmodel3では有意な違いは無いとわかります。
model3を見てみます。

avgAreaやavgGDPはp値が0.05ですが、avgAre:avgGDPなどの交差項のp値が0.05なので外せないです。残差プロットを見てみましょう。
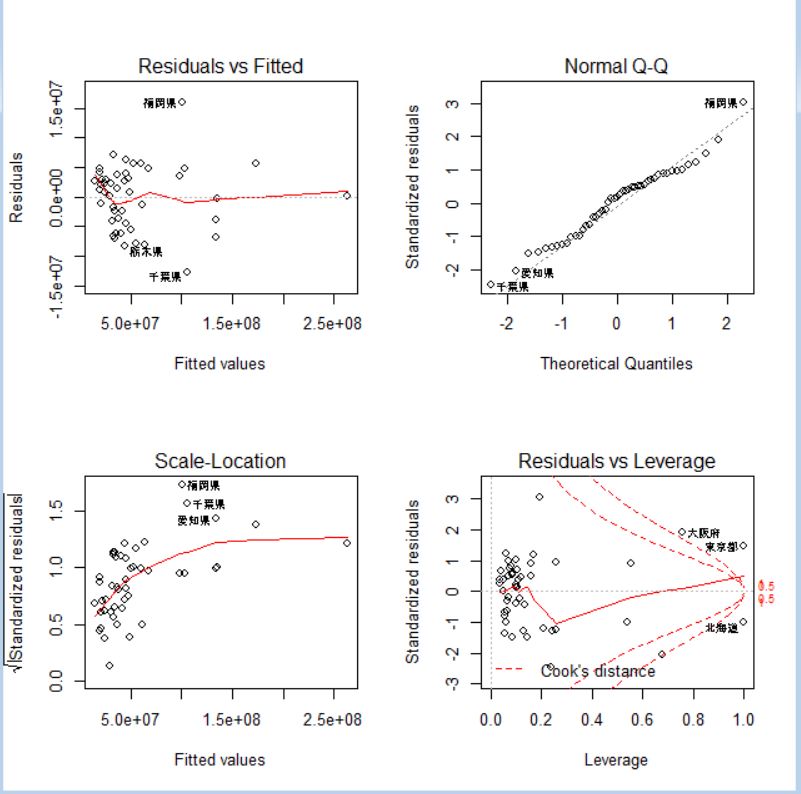
今度は、対数をとったデータ回帰分析してみましょう。

さきほどと同じような手順で不要な変数を削除していきます。まずは、logPop:logArea:logGDPですね。

anova関数でlmodel1とlmodel2を比較します。p値が0.5586ですから、二つのモデルに有意な違いはありません。なので、より単純なlmodel2をさらに詳しく調べます。

I(logArea^2)を削除しましょう。

p値は0.5492と0.05より大きいですから、lmodel2とlmodel3では有意な違いは無いです。lmodel3を見てみます。

除外できる変数はなくなりましたね。残差プロットを見てみましょう。

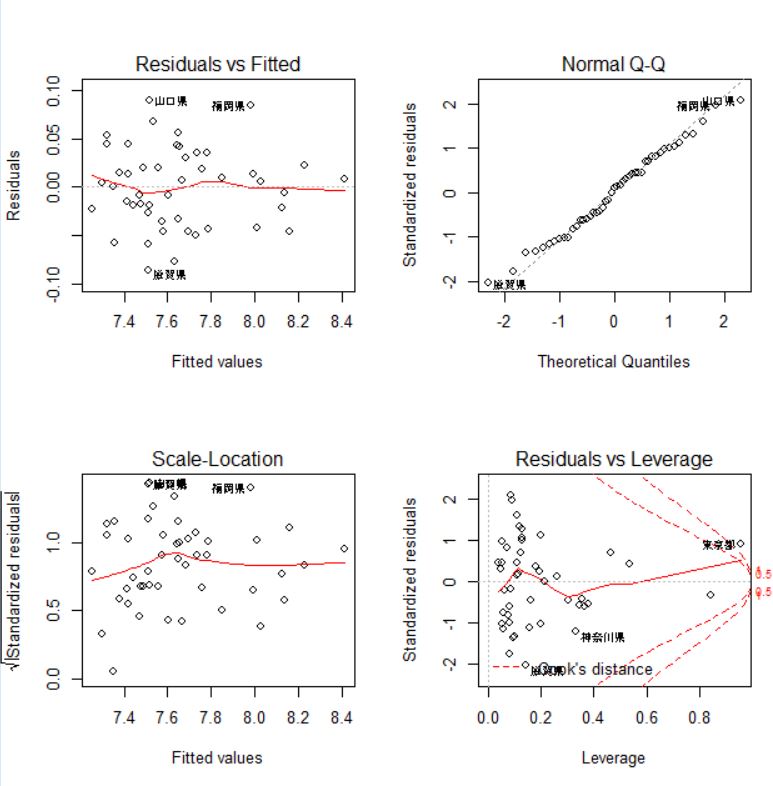
老人福祉費は重回帰分析でしたので、児童福祉費は単回帰分析をしてみます。
まずは、人口で回帰してみましょう。

avgPopのp値が0.202なので削除します。

p値が0.202なので、avgPopは無くても大丈夫ですね。ChildPop2を見てみます。

散布図の上に回帰線を描いてみましょう。
まずは、回帰線のxvを作成します。


今回は以上です。