www.crosshyou.infoの続きです。
今回は、人口1人当りの県内総生産額(perGDP), 人口10万人当りの第1次産業事業所数(per1st), 人口10万人当りの第2次産業事業少数、人口10万人当りの第3次産業事業所数の相関関係を見てみようと思います。

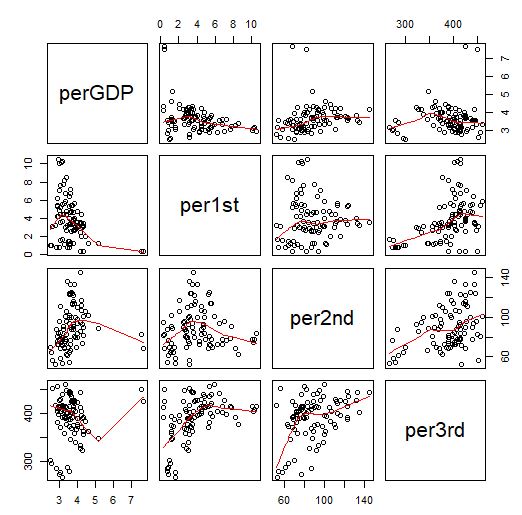
いちいち、df[ , c("perGDP", "per1st", "per2nd", "per3rd")]と指定するのは面倒なので、あらかじめ、idxcolという名前でこれら4つの変数名のインデックスを作り、df[ , idxcol]としてpairs関数で散布図マトリックスを描きました。
perGDPは他の変数とは関係あるのか、ないのかよくわからないですね。
cor関数で相関係数マトリックスを見てみます。
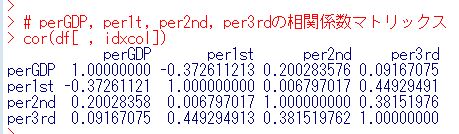
perGDPとper1stの相関係数は、-0.373です。負の相関です。per2ndとの相関係数は0.200です。正の相関です。per3rdとの相関係数は、0.092です。ほとんど無相関です。
perGDPとper1stとの回帰分析をlm関数でやってみましょう。前回の分析で2009年度と2014年度ではperGDPの値は違うようですから、Yearもexplanatory変数に入れます。
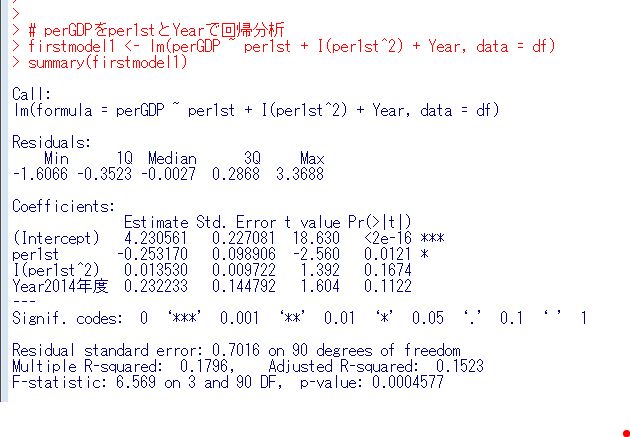
p-value = 0.0004577と0.05よりも小さいですから、有意なモデルです。I(per1st^2)を削除して単純にできそうです。

anova関数で、firstmodel1とfirstmodel2を比較しました。Pr(>F)が0.1674と0.05以上なのでfirstmodel2でもよさそうです。
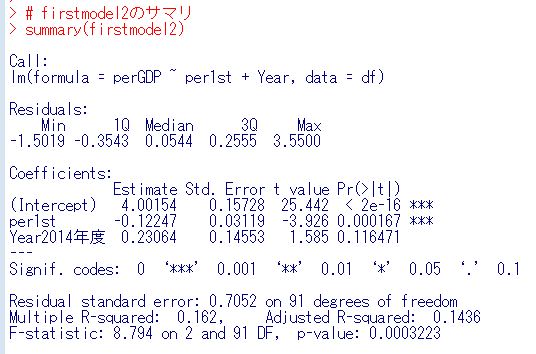
Yearも削除してよさそうです。
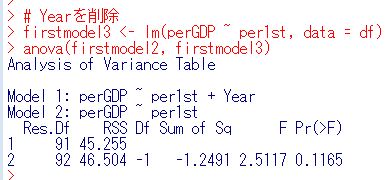
firstmodel3を見てみましょう。

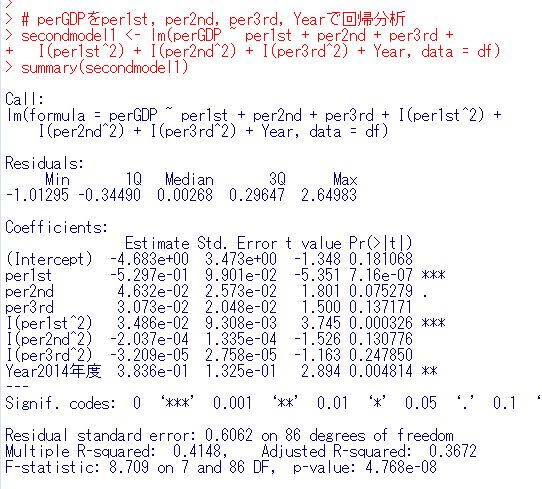
p-valueは0.000217と0.05よりも小さいので有意なモデルです。per1stの係数がマイナスですから、per1stが大きい都道府県ほど、perGDPは少ないとうことですね。
いままではper1stとYearが説明変数でしたが、per2ndとper3rdも説明変数に入れて回帰分析してみましょう。
step関数で単純化します。
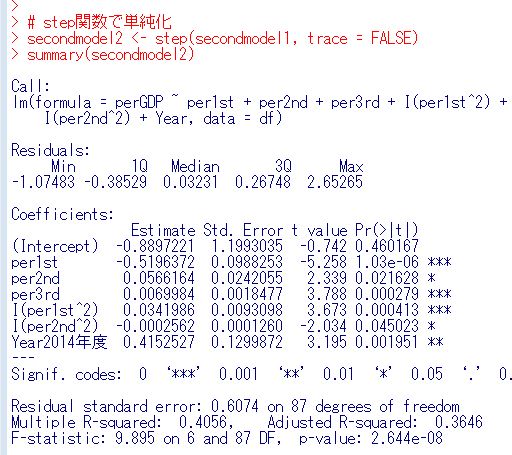
p-valueは2.644e-08なので0.05よりも小さいですから有意なモデルです。Multiple R squaredが0.4056となりました。per1stだけのモデルではMultiple r-squaredは0.1388なので大幅に上昇しました。
firstmodel3とsecondmodel2の残差プロットを見てみます。

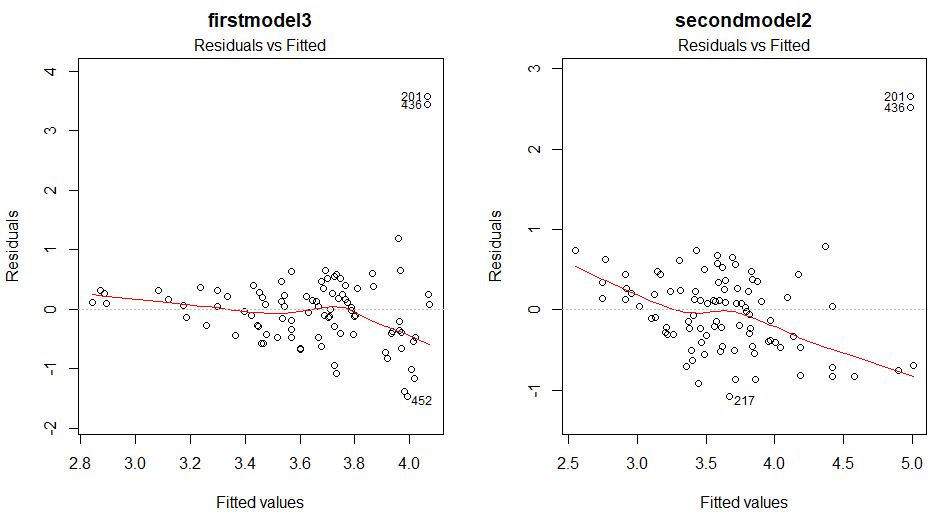
firstmodel3は値が大きくなるにつれて、残差も大きくなる傾向があります。これは良くない傾向です。secondmodelのほうが残差が小さいことがわかります。
箱ひげ図を並べて比較してみます。

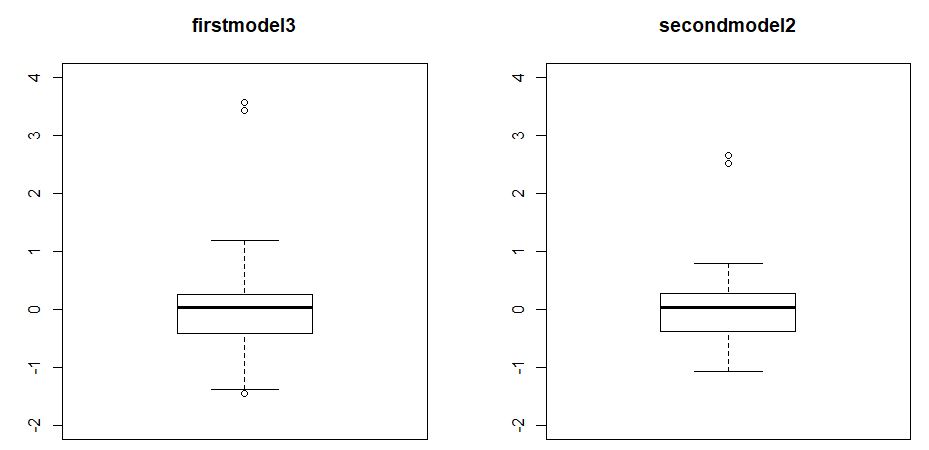
secondmodel2の箱ひげ図のほうがコンパクトですね。
今回は以上です。