今回は、男性の1日当りの所定内給与額と女性の1日当りの所定内給与額の回帰分析をしてみたいと思います。
こちらの本でbroomパッケージを使う方法を学んだので、その練習です。
まずは、全部のデータで、散布図を描いてみましょう。

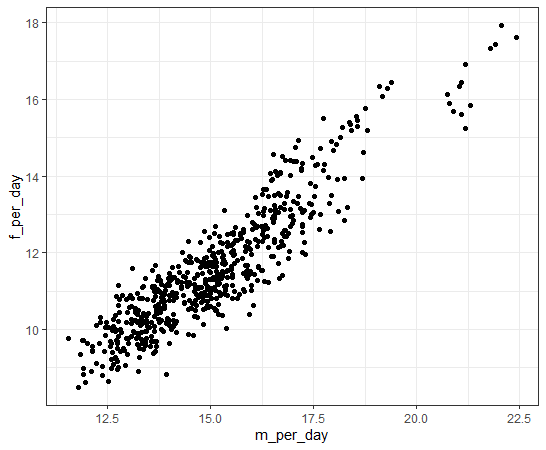
library(dslabs)とds_theme_set()でグラフの書式を設定しました。
その後にggplot関数とgeom_point関数で散布図を描きました。
年度ごとに分割して散布図を描いてみます。

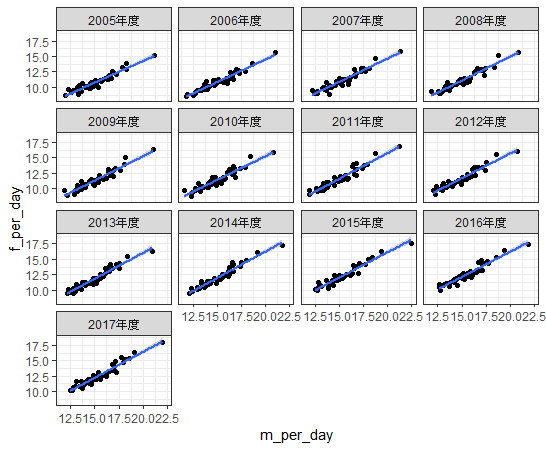
facet_wap関数で年度別にして、さらにgeom_smooth関数で回帰直線を付け足しました。年度による違いはあまりないようですね。
早速回帰分析をしてみます。
まずは、年度を関係なくしたモデルです。

p-valueは2.2e-16よりも小さく有意なモデルです。R-squaredは0.8314です。
m_per_dayのEstimate(係数)は0.80803です。m_per_dayが1000円上昇すると、f_per_dayは808円上昇します。
broomパッケージを読み込んで、glance関数でこのlm1を見てみましょう。
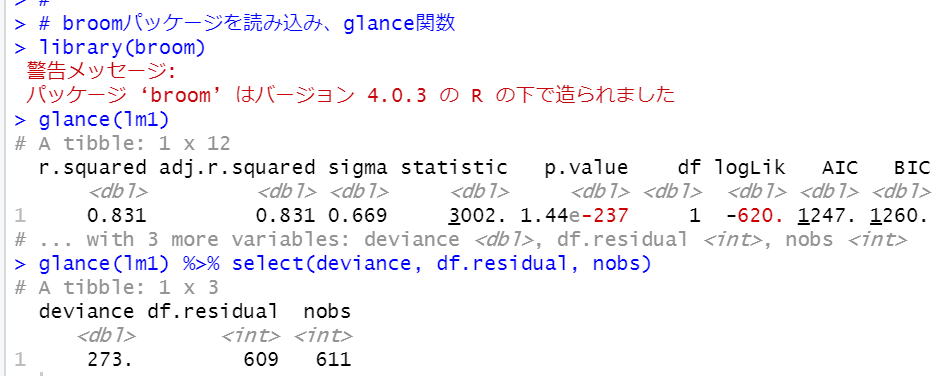
glance関数で回帰分析モデルを見ると、このようにtibbleとして結果が出力されます。
次は年度ごとにグループ化して回帰分析をしてみましょう。
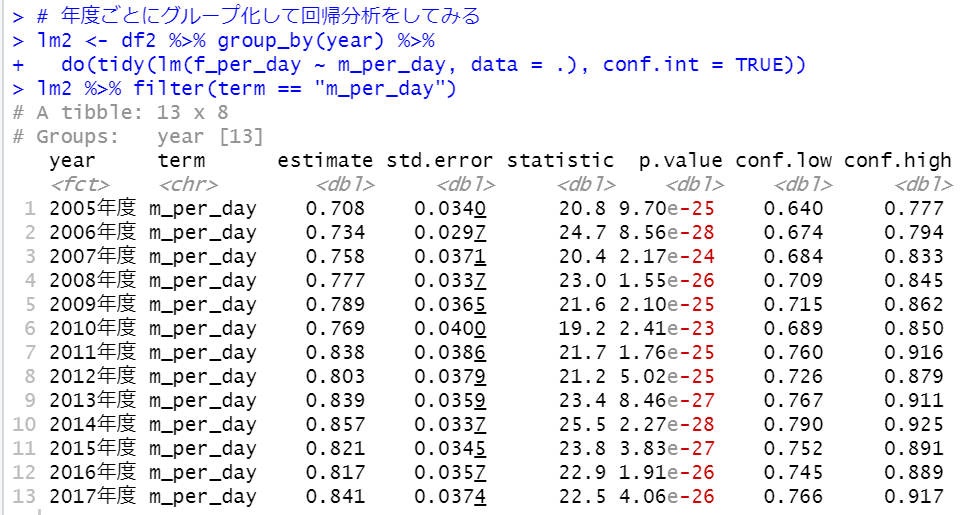
データフレーム、df2をgroup_by関数でyearでグループ化してから、do関数とtidy関数でlm関数を処理してtibbleとして結果を返しました。
estimateの列を見るとわかりますが、2005年度は0.708だったのが2017年度は0.841と男女の格差が知事待っていることがわかります。
interceptのほうもみてみましょう。
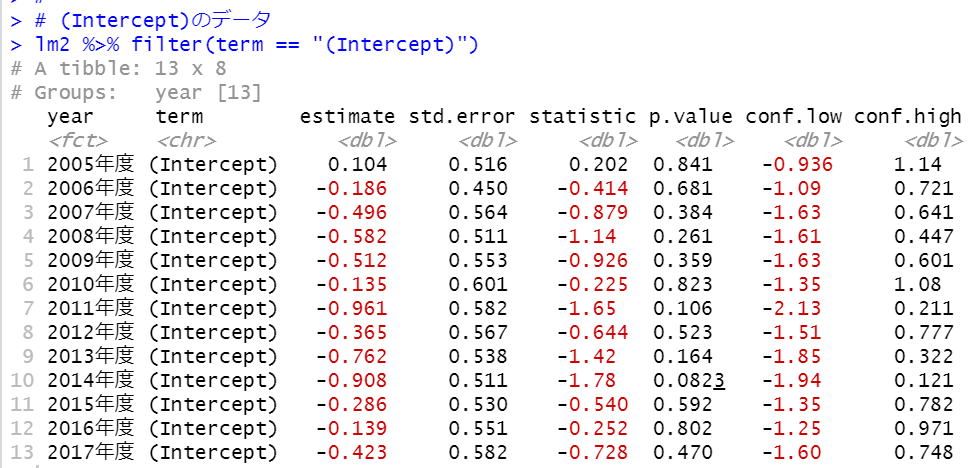
Interceptのほうはp.valueが全て0.05以上ですし、信頼区間も全て0を含んでいます。
それでは、m_per_dayのEstimate(係数)をグラフにしてみます。

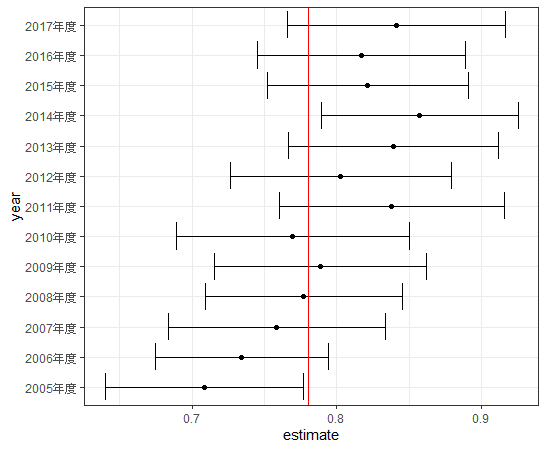
geom_errorbar関数で信頼区間のグラフになります。geom_point関数でEstimate(係数)を点で示し、geom_hline関数で0.78の水準に線を引いて信頼区間がかぶっているかどうかをわかりやすくしました。最後にcoord_flip関数で縦横は反転しています。
2005年度と2014年度の信頼区間はかぶっていないことがわかります。
全体のデータにyearも加えて回帰分析してみます。
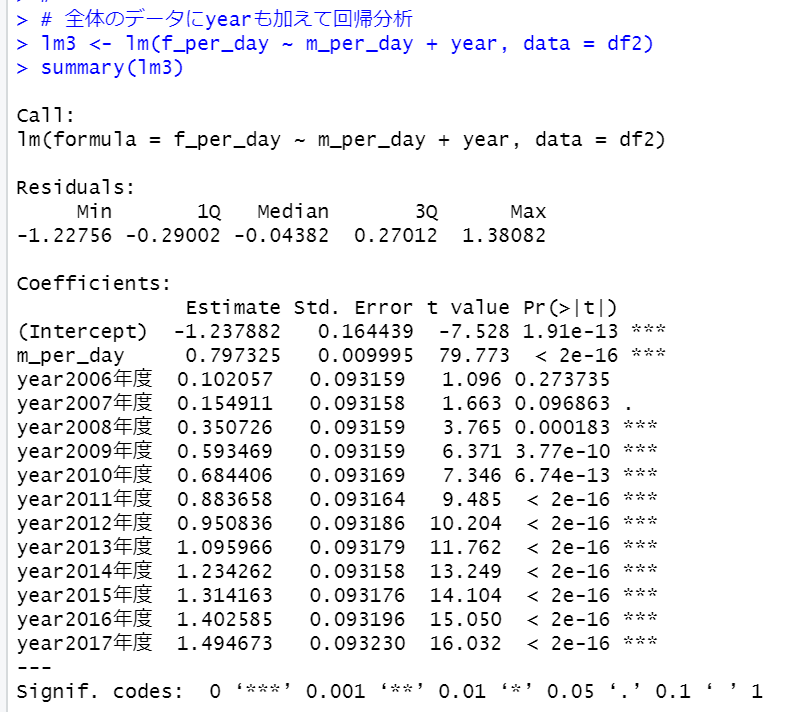

2005年度が基準です例えば、2005年度の回帰直線は u を誤差項とすると、
f_per_day = -1.237882 + 0.797325 * m_per_day + u です。
2017年度の回帰直線は
f_per_day = -1.237882 + 1.494673 * 0.797325 * m_per_day + u
男性の1日当りの所定内給与額が同じだとすると、女性の1日当りの所定内給与額は、2017年度のほうが平均して1500円ぐらい高い、ということですね。
今回は以上です。
次回は
です。
はじめから読むには、
です。
