
Photo by Kazden Cattapan on Unsplash
の続きです。前回はあんま・マッサージ師の変化幅をはり・きゅう師の変化幅で説明する単回帰モデルを分析しました。

R-squaredが0.4513ですので、あんま・マッサージ師の変化幅をはり・きゅう師の変化幅で45%ぐらい説明できるということです。
今回は他の説明変数を追加していって、R-squareがどのくらい変化するかみてみます。

あんま・マッサージ師の変化幅との相関を見ると、harikyu_pop_chgの次に相関関係が強い(絶対値ベース)のはanmassage_pop75です。1975年時点の人口100万人当たりのあんま・マッサージ師の人数です。これを説明変数に加えてみます。
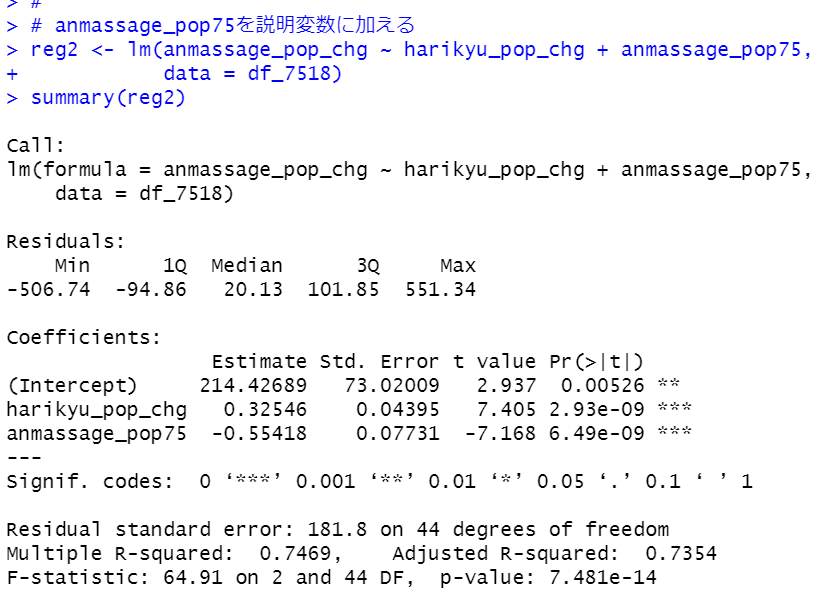
あんま・マッサージ師の変化幅 = 214 + 0.325 * はり・きゅう師の変化幅 - 0.554 * 1975年時点のあんま・マッサージ師の人数 + 誤差項
という推計結果になりました。
1975年のあんま・マッサージ師の人口100万人当たりの人数が100人のところは55人ぐらいあんま・マッサージ師が減る、ということです。半減してしまうということですからかなり大きな影響ですね。R-squaredは0.7649と上昇しました。
誤差項が均一分散になっているかどうか、bptest()関数で確認します。

p-valueが3.809e-05と0.05よりも小さいです。ということは、H0: 誤差項は均一分散である という帰無仮説が棄却されて誤差項は不均一分散している、ということです。
誤差項をプロットしてみます。
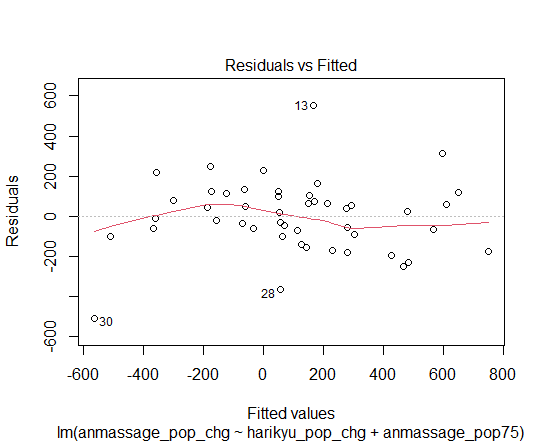
グラフは均一分散しているように見えますけどね。。。
stargazerパッケージのstargazer()関数で単回帰モデルと重回帰モデルを比較してみます。

harikyu_pop_chgの係数は、単回帰モデルだと0.383ですが、重回帰モデルだと0.325と少し小さくなっています。
さらに説明変数を加えてみます。harikyu_pop75を加えてみましょう。

あんま・マッサージ師の変化幅 = 142 + 0.35 * はり・きゅう師の変化幅 - 0.73 * 1975年時点のあんま・マッサージ師の人数 + 0.22 * 1975年のはり・きゅう師の人数 + 誤差項
という推計式になります。1975年のはり・きゅう師の係数のp値は0.08なので5%水準では有意ではないですが、10%水準では有意な値です。
bptest()関数で誤差項の不均一分散を検定しましょう。

p値が0.05よりも小さい値ですので、誤差項は均一分散しているとは言えないようです。
reg2のモデルとreg3のモデルを比較してみます。
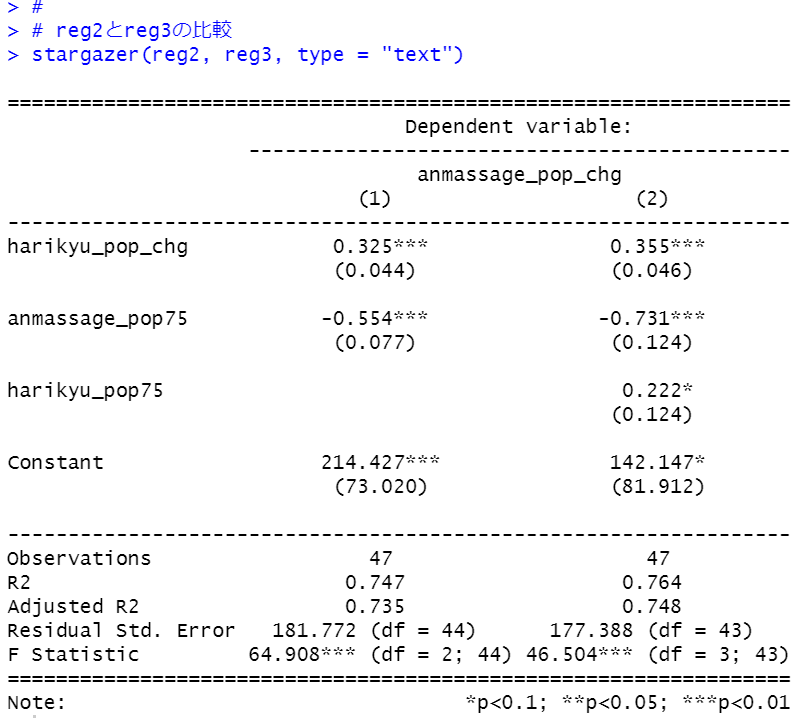
harikyu_pop_chgの係数が0.325から0.355に上昇して、anmassage_pop75の係数は-0.554から-0.731に下落しました。R2は0.747から0.764に、Adjusted R2は0.735から0.748になっています。
pop75: 1975年時点の人口を加えてみます。update()関数で追加します。
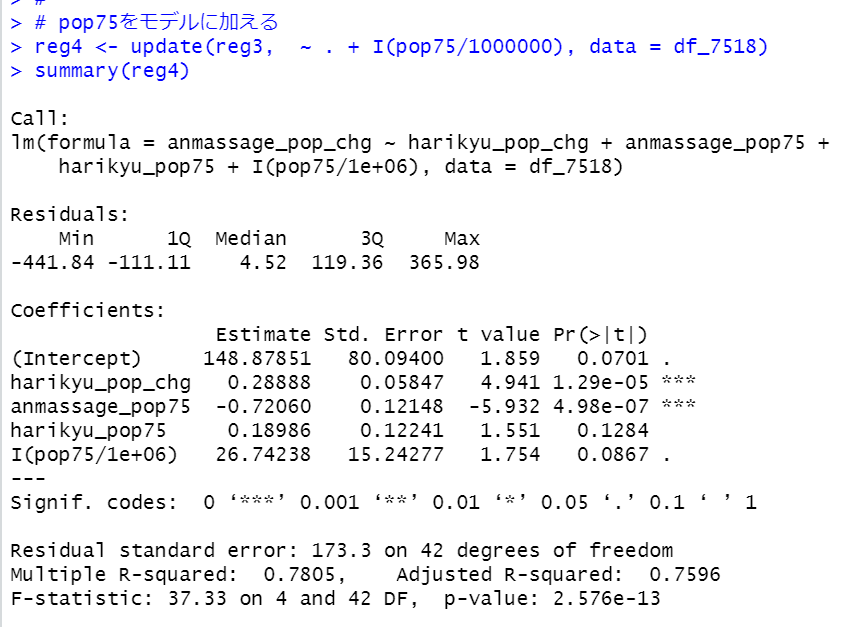
人口は100万人単位にしました。
あんま・マッサージ師の変化幅 = 149 + 0.29 * はり・きゅう師の変化幅 - 0.72 * あんま・マッサージ師の人数(1975年) + 0.19 * はり・きゅう師の人数(1975年) + 24.7 * 人口(1975年) + 誤差項
という推計結果です。1975年時点のあんま・マッサージ師の人数、はり・きゅう師の人数、人口が同じならば、100人はり・きゅう師が増えるとき29人あんま・マッサージ師が増えるということですね。
bptest()関数で誤差項の不均一分散を調べます。

このモデルも不均一分散のようですね。
reg3とreg4を比較してみます。
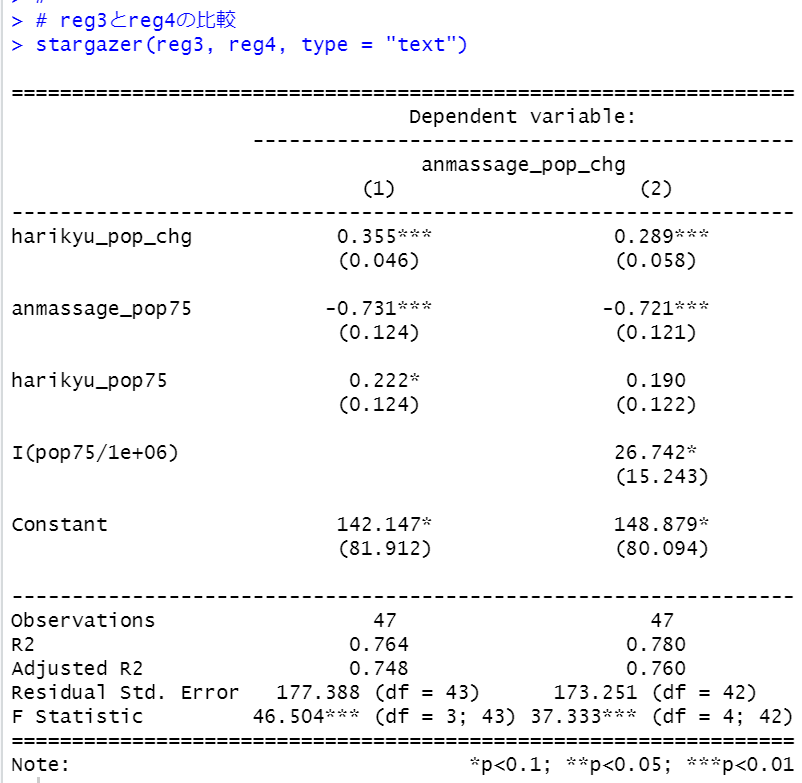
harikyu_pop_chgの係数は0.355から0.289になりました。
R2は0.764から0.780に、Adjusted R2は0.748から0.780になりました。
judo_pop_chgを加えてみます。
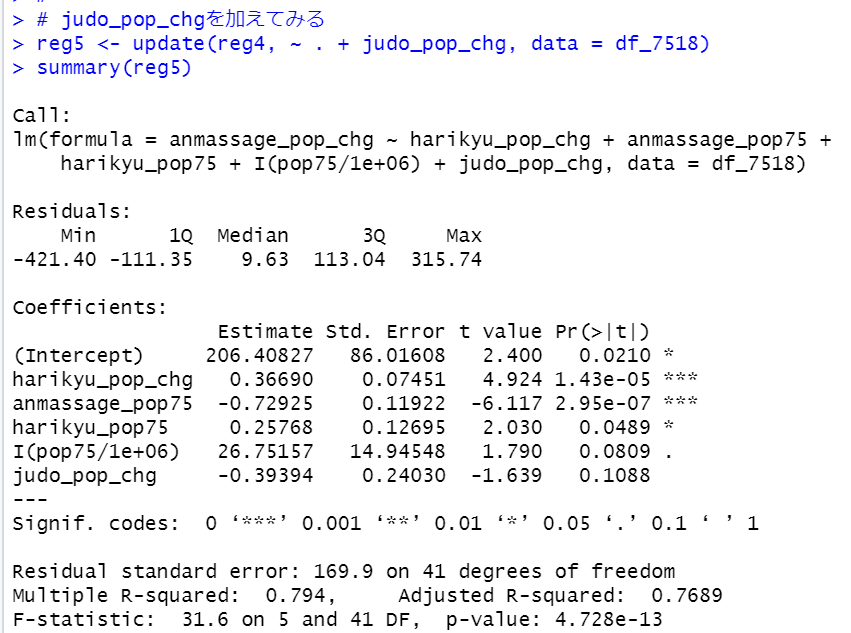
あんま・マッサージ師の変化幅 = 206 + 0.37 * はり・きゅう師の変化幅 - あんま・マッサージ師の人口(1975年) + 0.26 * はり・きゅう師の人口(1975年) + 26.7 * 人口(1975年) - 0.39 * 柔道整復師の変化幅 + 誤差項
というモデルです。他の条件が同じならば、はり・きゅう師の変化幅が100人だとあんま・マッサージ師の変化幅は37人ということですね。
bptest()関数で誤差項の不均一分散を調べます。

誤差項は不均一分散しているようです。
reg4とreg5を比較します。
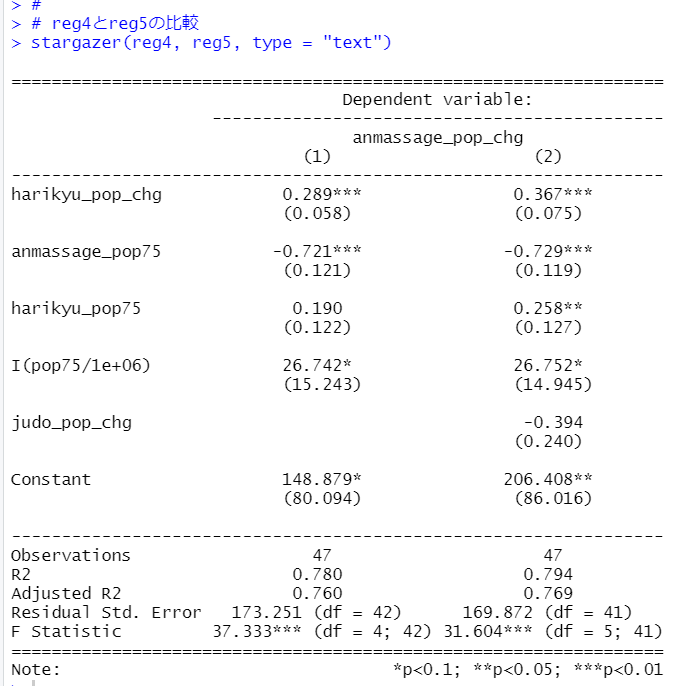
harikyu_pop_chgの係数が0.289から0.367に増えました。R2は0.780から0.794に、Adjusted R2は0.760から0.769になりました。
judo_pop75を加えます。

あんま・マッサージ師の変化幅 = 152 + 0.41 * はり・きゅう師の変化幅 - 0.84 * あんま・マッサージ師の人数(1975年) + 0.34 * はり・きゅう師の人数(1975年) + 20.8 * 人口(1975年) - 0.48 * 柔道整復師の変化幅 + 0.98 * 柔道整復師の人数(1975年) + 誤差項
という推計式になりました。他の条件が同じならば、100人はり・きゅう師の人数が増えると、41人あんま・マッサージ師の人数が増える計算になります。
bptest()関数で誤差項の不均一分散を調べます。

p-valueが0.05よりも大きいので、5%の有意水準で、帰無仮説:誤差項は均一分散である、を棄却できません。よかったです。
stargazer()関数でreg1の単回帰モデルとreg6の重回帰モデルを比べましょう。どちらも誤差項は不均一分散していないです。
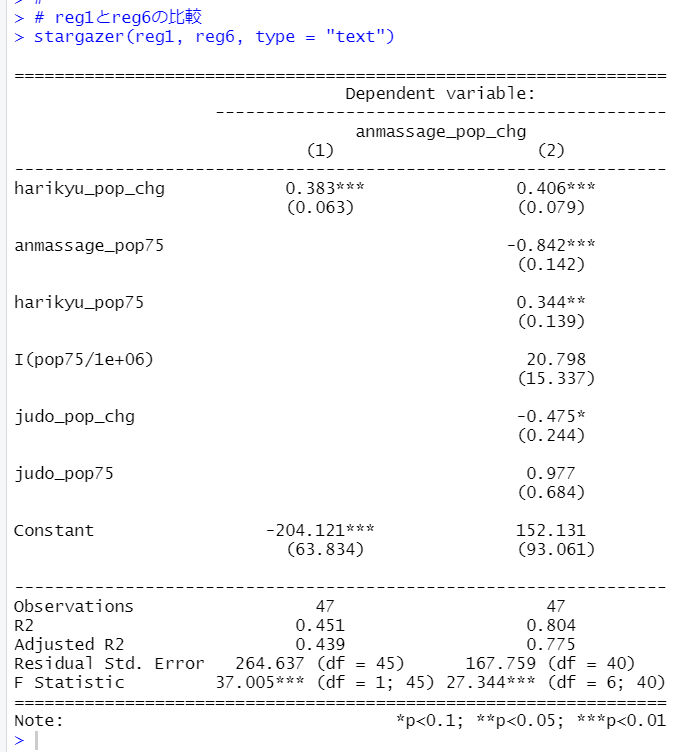
reg6、reg1のモデルの推計値と実際の値を散布図にしてみます。

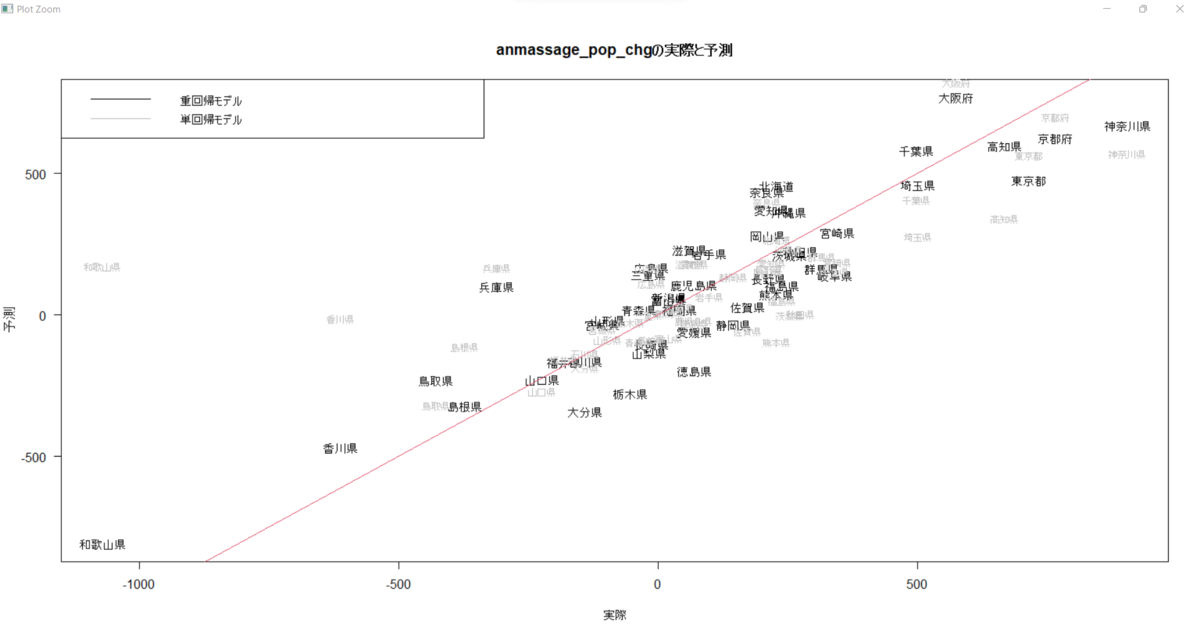
reg6, 重回帰モデルのほうが実際の値に近いことがわかります。和歌山県や香川県で顕著です。
今回は以上です。
次回は
です。
初めから読むには、
です。