
Photo by Marina Kraus on Unsplash
RのHIstDataパッケージのCavendishのデータは、イギリスの科学者のヘンリー・キャベンディッシュの1798年に行った地球の密度の測定に関する実験のデータです。
Wikipediaによると、
「1797から1798年にかけて、いわゆる「キャヴェンディッシュの実験」を行い、地球の比重を測定し、その結果を1798年に発表した。後年の科学者は、この実験の結果と万有引力の法則から万有引力定数が算出できることに気付いた。キャヴェンディッシュ自身は万有引力定数を算出したわけではないが、今日ではこの実験は「地球の密度を測定した」というよりは「万有引力定数を測定した」と捉えられていることが多い。」
とのことです。
それではヘルプに出ているコードを実践していきます。
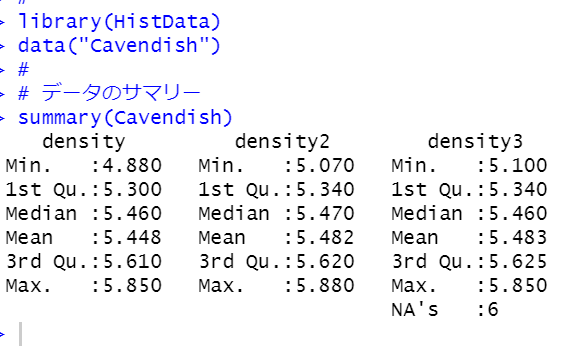
density, density2, density3という3つの変数があって、それぞれ同じような値の変数ですね。
次のコードは、

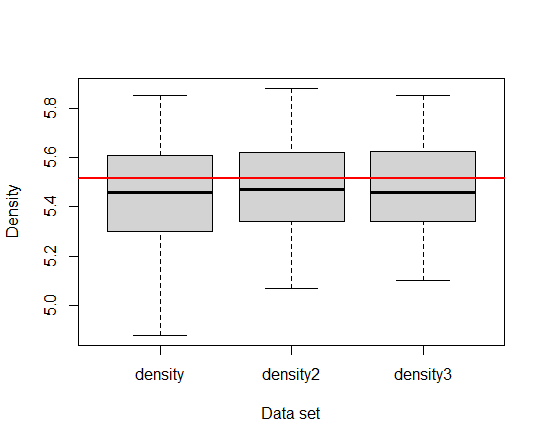
boxplot()関数で箱ひげ図を描き、abline()関数で水平線を描きました。
5.517というのは意味のある値だと思いますが、よくわからないです。後日調べて更新します。
次のコードはtrimmed meanを求めています。

sapply関数で3つの変数のtrimmed meanをいっぺんに計算しています。
一つ一つ計算するなら、

こんな感じでしょうか。
そして次のコードは、

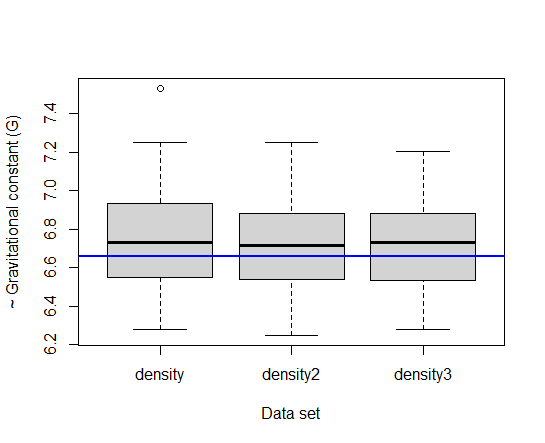
です。重力定数Gを計算するファンクションを作成して、Dという引数にCavendishのデータを代入して箱ひげ図を描いています。
以下がヘルプにあるコードです。
library(HistData)
data(Cavendish)
summary(Cavendish)
boxplot(Cavendish, ylab='Density', xlab='Data set')
abline(h=5.517, col="red", lwd=2)
# trimmed means
sapply(Cavendish, mean, trim=.1, na.rm=TRUE)
# express in terms of G
G <- function(D, g=9.806, R=6371) 3*g / (4 * pi * R * D)
boxplot(10^5 * G(Cavendish), ylab='~ Gravitational constant (G)', xlab='Data set')
abline(h=10^5 * G(5.517), col="red", lwd=2)