
Photo by Annie Spratt on Unsplash
の続きです。
前回は、log(GdpPop) = beta_0 + beta_1 * log(EdPop) + beta_2 * log(Area) + u という重回帰分析のモデルを考えました。
回帰分析で重要な仮定の一つが「誤差項の分散が独立変数とは関係なく一定の値である」というものです。
これがこの回帰モデルで成り立っているかどうかをチェックします。
まず。回帰モデルの推計式から求められる残差を変数として保存します。

残差はresid()関数で取り出すことができます。
残差の平均値は0であることを確認しましょう。

残差の平均値が0なので、残差の分散は、sum(残差の2乗)/(n - 1)です。なので、残差の2乗が独立変数と関係なければ、誤差項の分散は一定の値とみなすことができます。
lm()関数で回帰分析をします。
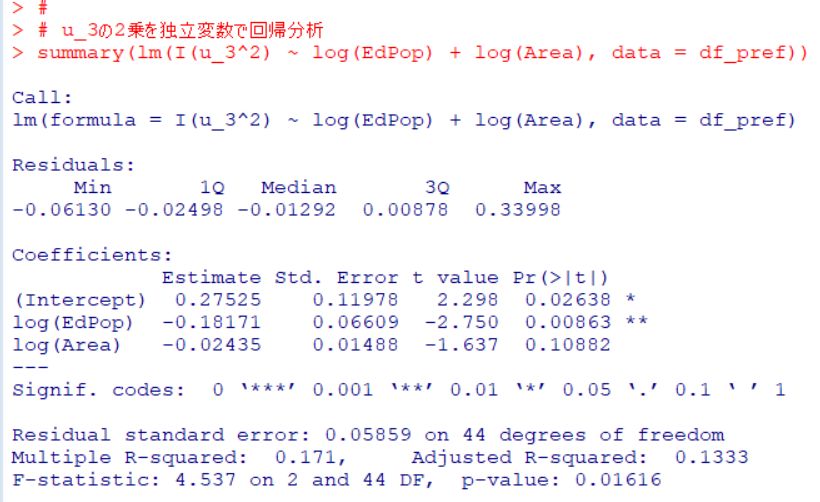
log(EdPop)の係数が有意に0ではないので、誤差項が均一分散していないです。
lmtestパッケージの中にある bptest()関数でも誤差項の均一分散のチェックができます。
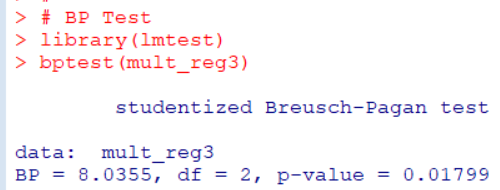
p-valueが0.01799と0.05よりも小さいので、H0: 誤差項は均一分散である。 という帰無仮説を棄却して、誤差項は均一分散ではない、という結論になります。
誤差項が均一分散でないときは、係数の有意性の判断は通常のsummary()関数の結果では得られないので、carパッケージのhccmとlmtestパッケージのcoeftest()関数を使います。
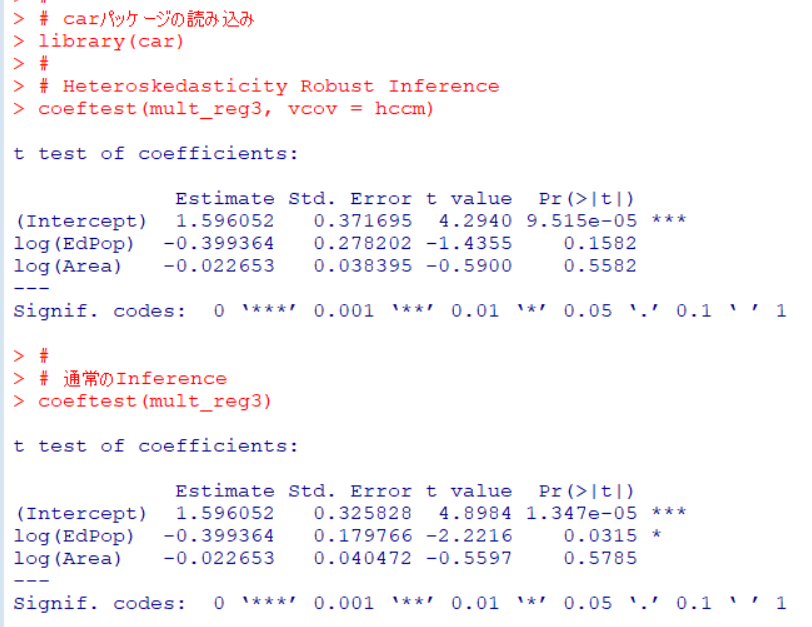
誤差項の不均一分散を考慮して係数の有意性をチェックすると、前回の通常の有意性のチェックでは有意になっていたlog(EdPop)が有意でなくなりました。
前回の結果では、一人当たりの教育費が増えると一人当たりの県内総生産額が減るという、少し納得のいかない結果でしたが、そうではないということですね。
今回は以上です。
次回は
です。
初めから読むには、
です。