東証一部の規模別・業種別PERとPBRのデータの分析１０ - PERを利益、資産、時間軸で重回帰分析する

www.crosshyou.infoの続きです。

今回はPERを利益、資産、時間軸で重回帰分析したいと思います。

参考書籍は

Statistics: An Introduction Using R

 です。

全体のデータだけで調べようと思います。

まずは、str関数、head関数、summary関数でもともとのデータフレームはどんなデータか確認します。

 3000の観測と12の変数があります。

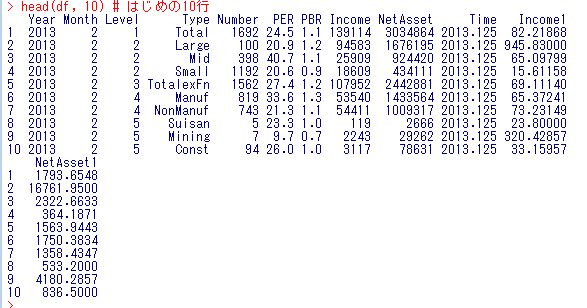
Levelは1から5まであります。

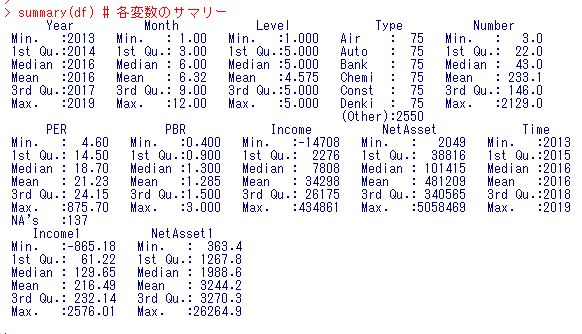
2013年から2019年ですね。

今回は、Level1, Totalだけで考えたいと思います。

まずは、作業用のデータフレームを作成します。

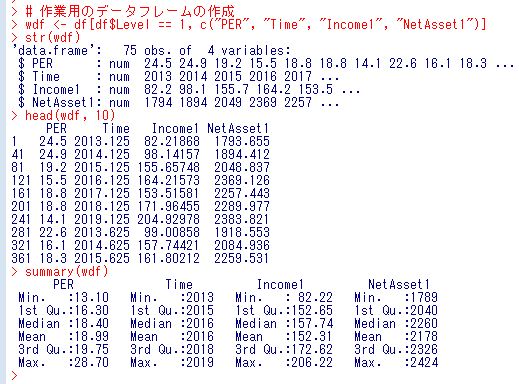
はじめに、pairs関数でそれぞれの変数どうしの散布図を描きます。

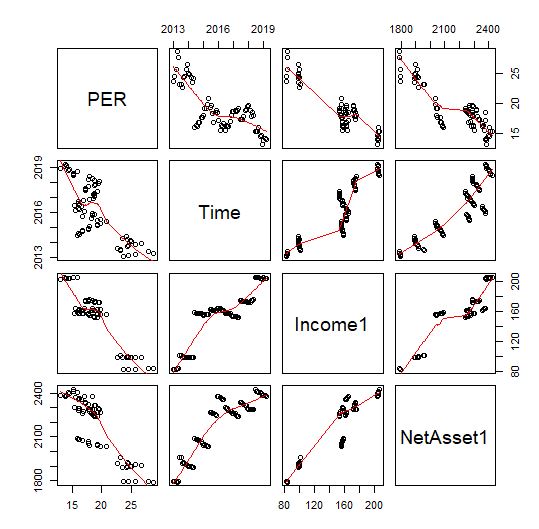
cor関数で相関マトリックスを作成します。

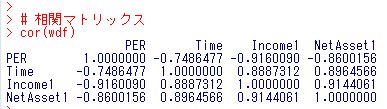
それぞれの変数どうしは相関があることがわかります。

まずは、Time, Income1, NetAsset1とそれぞれの交差項と二乗項を考慮したfull modelから分析しましょう。lm関数を使います。

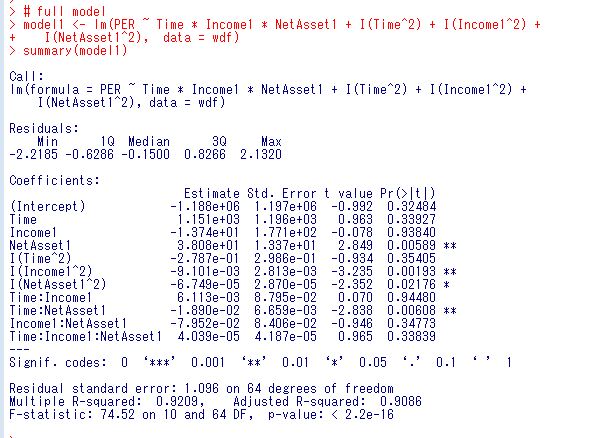
Time:Income1:NetAsset1は有意ではないようなので、削除したモデルを考えましょう。

update関数を使います。

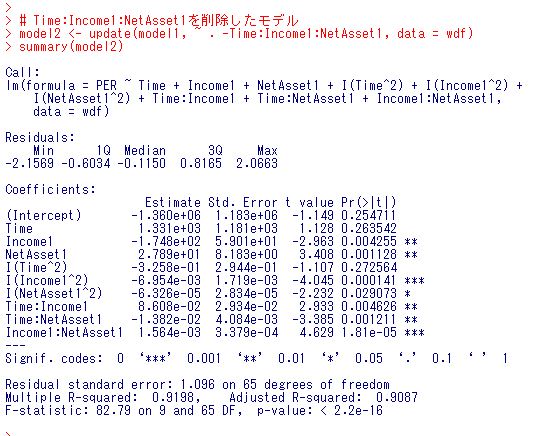
I(Time^2)は有意ではないようです。これを削除したモデルを考えましょう。

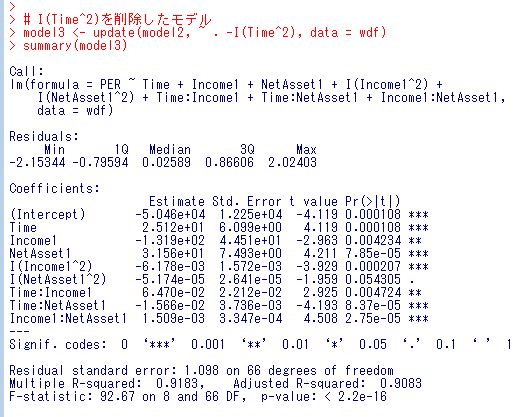
I(NetAsset1^2)も有意ではないようです。削除したモデルを考えましょう。

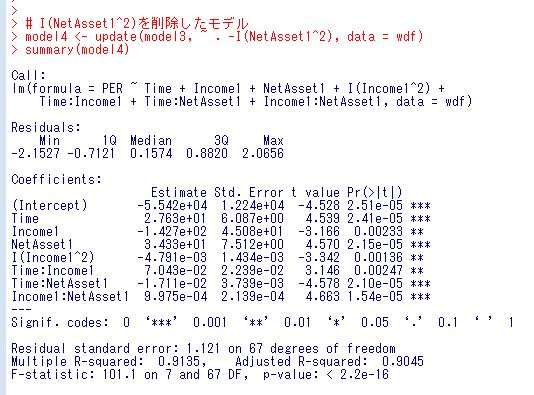
これですべての係数が有意なモデルとなりました。残差プロットのグラフを描いてみます。。

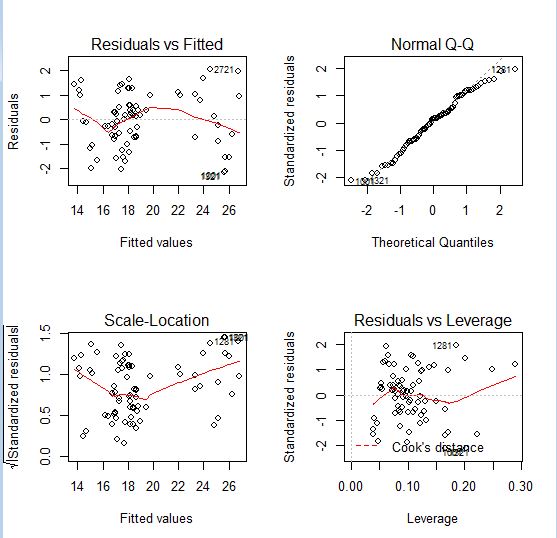
最後の実績のPERとmodel4で計算されたPERをグラフにして比較します。

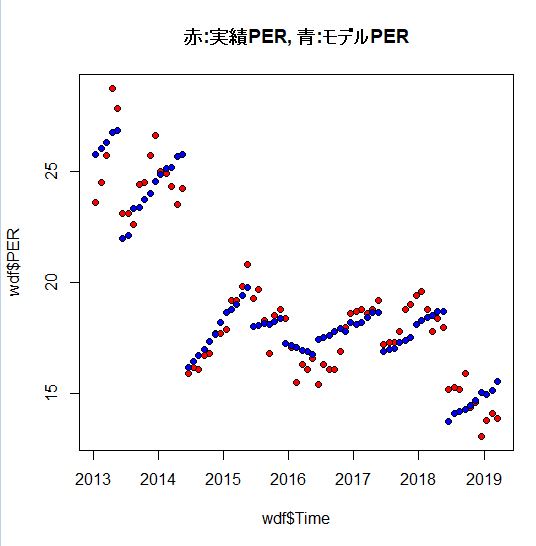
今回は以上です。

最後のwdfを消去します。rm関数です。

 次回は

www.crosshyou.info

です。

今回のR言語のコードです。

# データフレームの確認
str(df) # 構造の確認

head(df, 10) # はじめの10行

summary(df) # 各変数のサマリー

# 作業用のデータフレームの作成
wdf <- df[df$Level == 1, c("PER", "Time", "Income1", "NetAsset1")]
str(wdf)
head(wdf, 10)
summary(wdf)

# 変数どうしの散布図
pairs(wdf, panel = panel.smooth)

# 相関マトリックス
cor(wdf)

# full model
model1 <- lm(PER ~ Time * Income1 * NetAsset1 + I(Time^2) + I(Income1^2) +
I(NetAsset1^2), data = wdf)
summary(model1)

# Time:Income1:NetAsset1を削除したモデル
model2 <- update(model1, ~ . -Time:Income1:NetAsset1, data = wdf)
summary(model2)

# I(Time^2)を削除したモデル
model3 <- update(model2, ~ . -I(Time^2), data = wdf)
summary(model3)

# I(NetAsset1^2)を削除したモデル
model4 <- update(model3, ~ . -I(NetAsset1^2), data = wdf)
summary(model4)

# model4の残差プロット
par(mfrow = c(2, 2))
plot(model4)
par(mfrow = c(1, 1))

# X軸Time, Y軸PER
plot(wdf$Time, wdf$PER, pch = 21, bg = "red", main = "赤:実績PER, 青:モデルPER")
points(model4$model2, model4$fitted.values, pch = 21, bg = "blue")

# wdfの削除
rm(wdf)