
Photo by Adam Śmigielski on Unsplash
の続きです。
複数のグラフを一度に表示したいので、gridExtraというパッケージを読み込みます。
続いて、各変数の密度分布グラフを描きましょう。
まず、pop: 総人口(人)です。populationのpopです。


人口のデータは対数をとったほうが正規分布に近くなりますね。
mar: 婚姻件数はどうでしょうか?marriageのmarです。

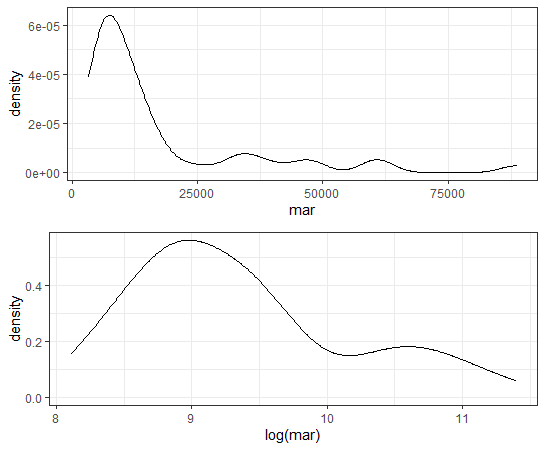
婚姻件数も対数をとったほうが正規分布に近くなりますね。
div: 離婚件数はどうでしょうか?divorceのdivです。

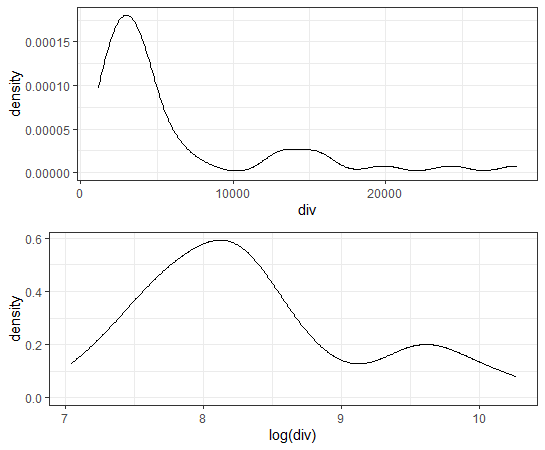
離婚件数も対数にしたほうが正規分布に近くなります。
gdp: 県内総生産額(平成17年基準・百万円単位)はどうでしょうか? gdpはGDP(Gross Domestic Product)の意味です。

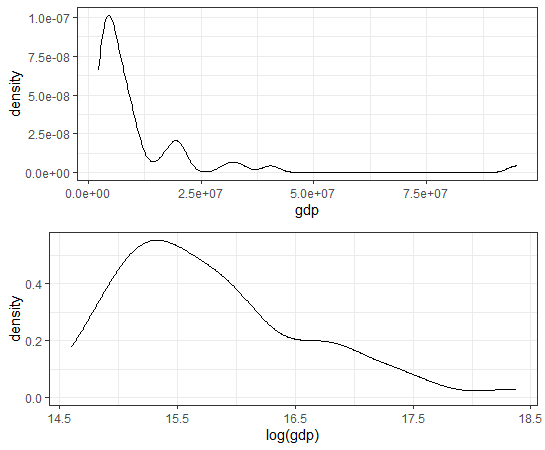
県内総生産額も対数変換したほうが正規分布に近くなりますね。
sch: 中学校数(校)はどうでしょうか?schoolだからschです。
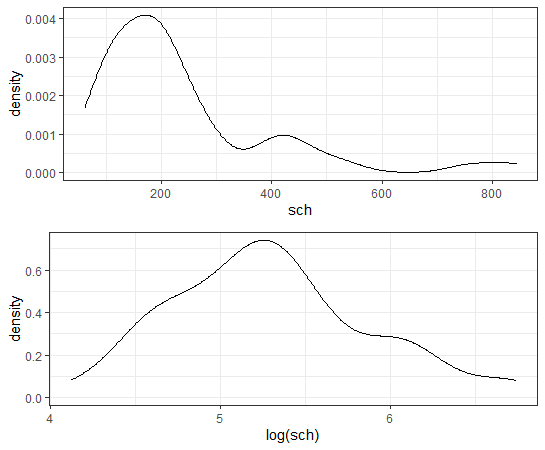
中学校の数も対数変換したほうが正規分布に近くなります。
lei: 行楽行動者率(15歳以上)(%)はどうでしょうか?leisureのleiです。
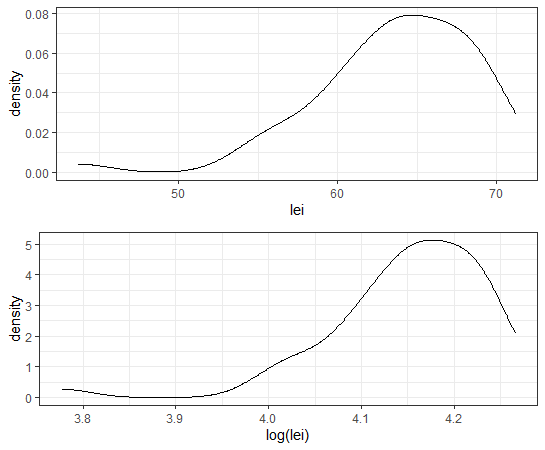
行楽行動者率は絶対数ではなくて比率ですので、対数変換してもしなくてもあまり分布の形状はかわらないですね。
以上を踏まえて、pop, mar, div, gdp, schを対数変換した変数を作ります。mutate()関数とlog()関数を使います。

散布図のマトリックスを描こうと思います。psychパッケージを読み込みます。

そうしたら、pairs.panels()関数を使います。

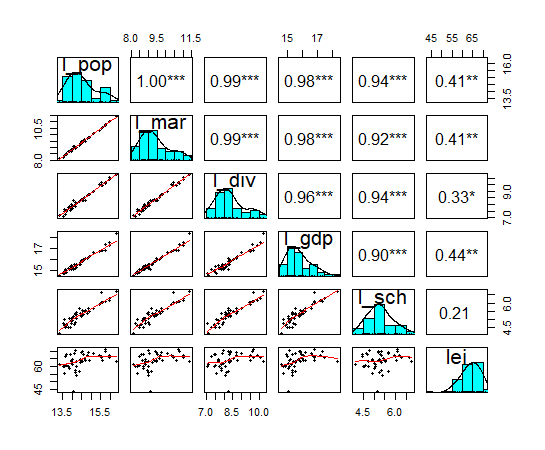
leiを除くと他のものは相関係数が0.9以上でみんな高い相関ですね。
あとで回帰分析をしようと思っているのですが、こんなに相関が高いのは困るので、新しい変数を作ります。

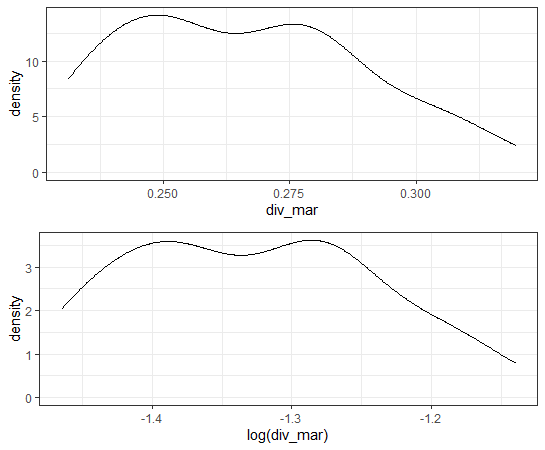
まず、離婚件数/(婚姻件数+離婚件数)という変数を作りました。離婚レシオとでもいいましょうか?値が大きいほど、婚姻件数と比較して離婚件数が多いという変数ですね。
密度分布グラフを見ると、対数に変換する必要はないようです。
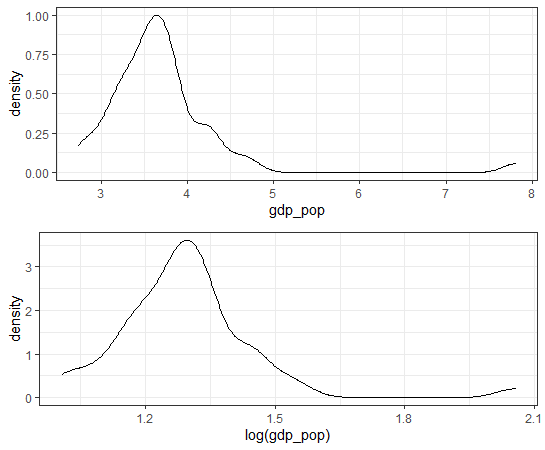
gdp/popで1人当たりGDPを作りました。上の密度分布グラフを見ると、4(百万円)の少し下ぐらいにピークがありますね。これは対数変換したほうが良さそうですね。対数変換した変数も作っておきます。


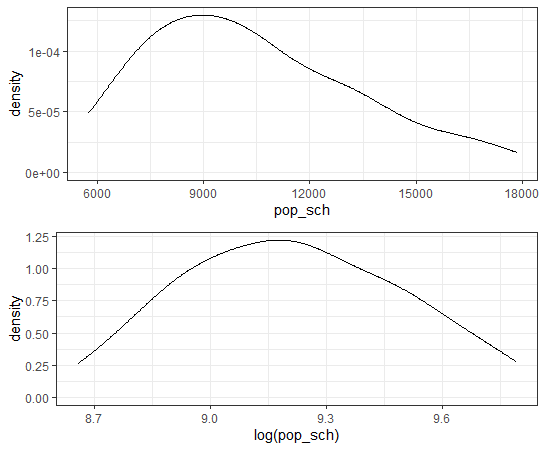
pop/schで人口何人で中学校が1校あるのか、という指標を作りました。上のグラフを見ると9000人ぐらいのところにピークがありますね。これも対数変換した値のほうがより正規分布にというか、左右対称に近い感じですね。対数変換した変数も作っておきます。

こうして作成した、変数での相関を見てみます。

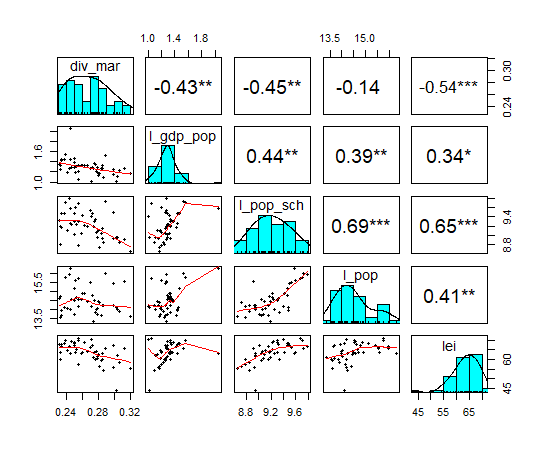
なんとなく適度に相関している感じになっていますね。
今回は以上です。
次回は
です。
初めから読むには、
です。