
Photo by Alex Quezada on Unsplash
前回は時系列データを回帰分析モデルで分析しました。
今回はそのモデルのSerial Correlationの有無をチェックします。
前回は、3つのモデルを作成してパラメータをOLSで推計しました。
OLSでの推計値は、Serial Correlationがあると正しく推計できません。
残差 = beta_0 + beta_1 * L(残差) + u
という一つ前の残差で残差を説明するというモデルを考えて、このbeta_1が有意ならばSerial Correlationがあるということです。
まずは、static_mod: Gdp = beta_0 + beta_1 * Ed + beta_2 * P_ration + u からチェックします。
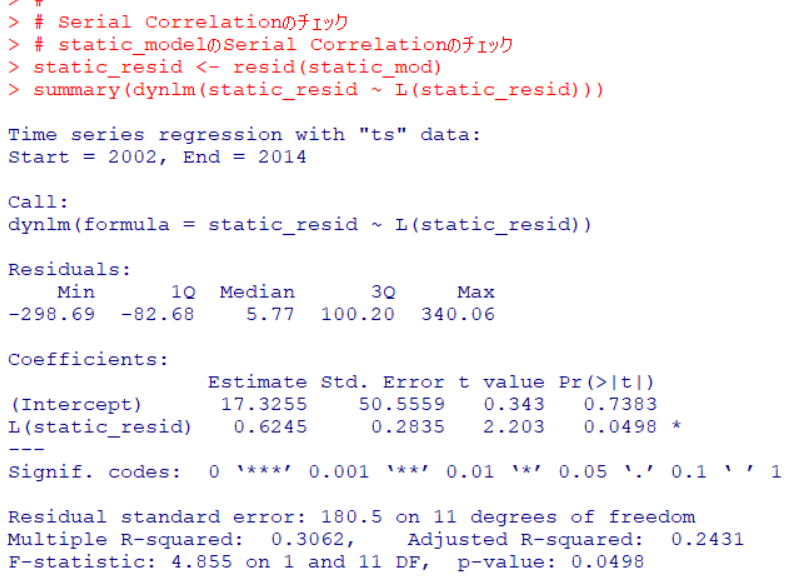
resid()関数で残差を取り出して、dynlm()関数でL()を使って残差の1つ前のラグで残差を回帰分析しています。L(static_resid)のp値が0.0498なのでSerial Correlationがある、ということですね。
次は、trend_mod: Gdp = beta_0 + beta_1 * Ed + beta_2 * P_ratio + beta_3 * trend + u
のSerial Correlation の有無をチェックします。
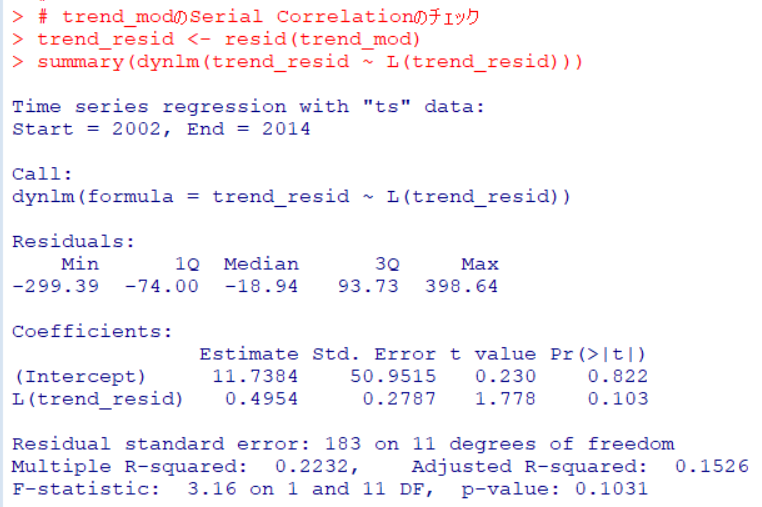
L(trend_resid)のp値は0.103と0.05よりも大きいので、Serial Correlation があるとは言えないです。
3つ目のモデル、lag_mod: Gdp = beta_0 + beta_1 * Ed + beta_2 * L(Ed) + beta_3 * P_ratio + beta_4 * L(P_ratio) + beta_5 * trend + u のSerial Correlationの有無をチェックします。
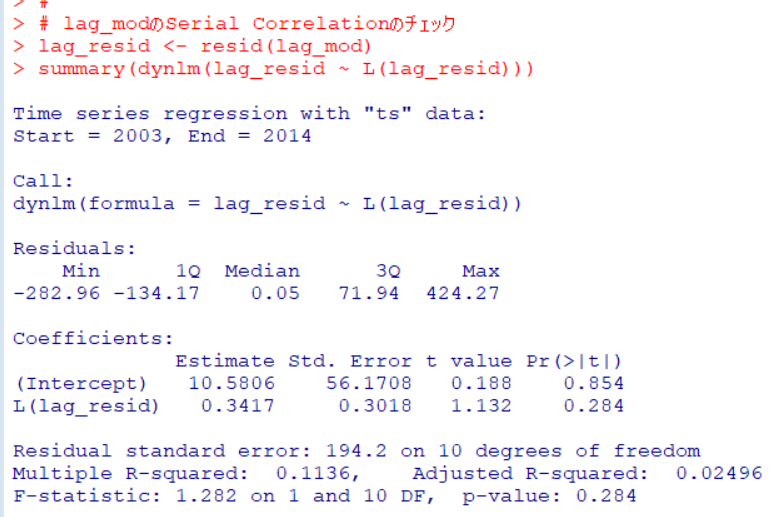
こちらもp値は0.284なので、Serial Correlationがあるとは言えないですね。
せっかくなので、三つの残差をグラフにしてみます。

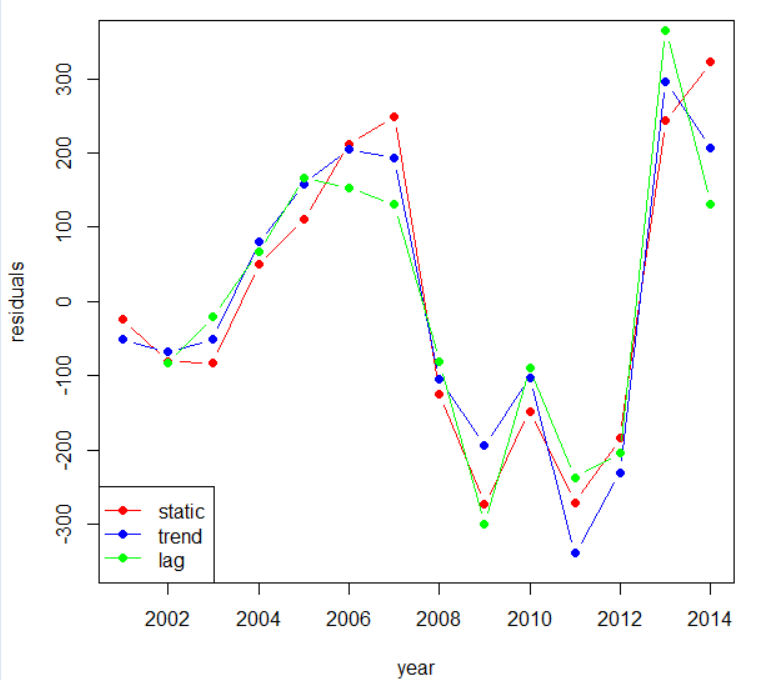
staticの残差はSerial Correlation有りと判定されて、trendとlagは有るとは言えないと判定されました。このグラフを見るだけでは、判断がつかいないですね。
今回は以上です。
次回は、
です。
はじめから読むには、
です。