
Photo by Colin Watts on Unsplash
の続きです。
今回はパネルデータ分析をします。
まず、plmパッケージを読み込みます。
このplmパッケージを使うとパネルデータ分析が簡単にできます。
まずは、通常のデータフレームをpdata.frame()関数でパネルデータに変換します。

pdata.frame(データフレーム, index = c("個別の変数", "時間の変数"))という構文です。
pdim()関数でパネルデータになったかどうかを見てみます。
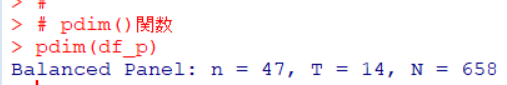
n = 47 となっています。47の都道府県がありますね。 T = 14 となっているので、14年間のデータだとわかります。Balanced Panelとあるので、47の都道府県のデータが14年分全部揃っていることがわかります。全部で観測数は 658 です。
それでは、回帰分析してみます。
はじめは、パネルデータなんだけども通常のクロスセクションのデータとみなして普通に回帰分析してみます。pooling cross section regression です。
plm()関数でパネルデータの回帰分析ができますが、model = "pooling" とするとpooling cross section regressionになります。
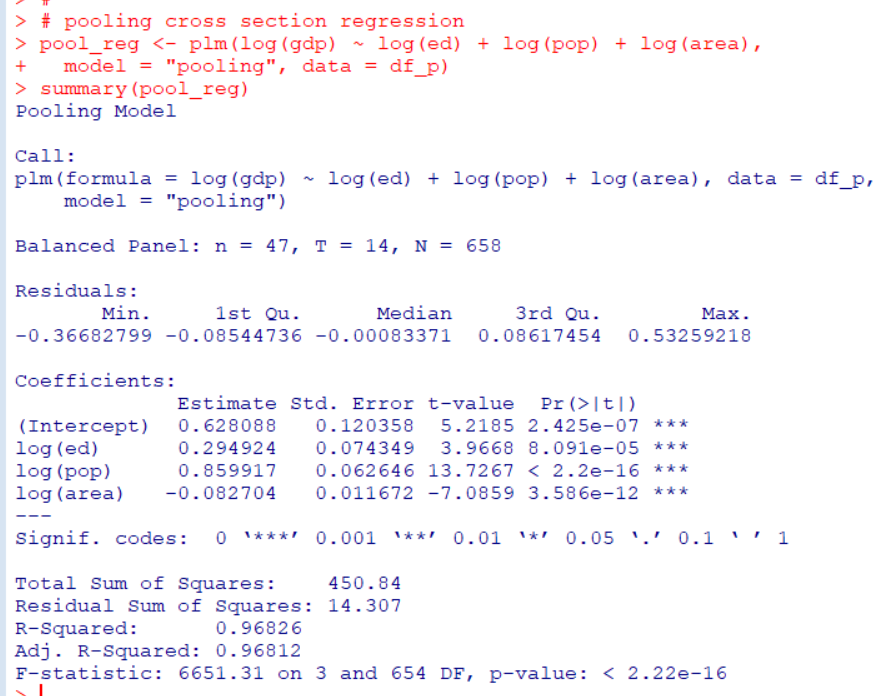
log(gdp) = 0.628 + 0.295 * log(ed) + 0.860 * log(pop) - 0.083 * log(area) + u
というモデルが推測できました。pop: 人口とarea: 住居可能面積が同じならば、ed: 教育費が1%上昇すると、gdp: 県内総生産額が0.295%上昇すると解釈できます。3つの係数はすべて0.1%水準で有意でした。
次は、model = "fd"として、first differenced estimator で係数を推計してみます。
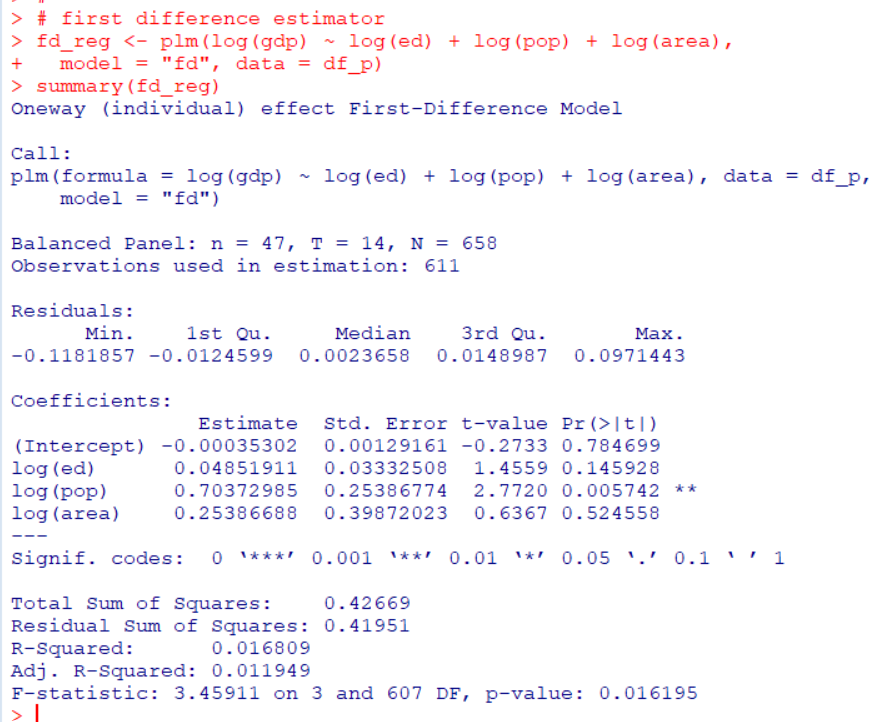
log(gdp) = -0.000 + 0.049 * log(ed) + 0.704 * log(pop) + 0.254 * log(area) + u
と推計できました。log(ed)は有意ではなくて、log(pop)の0.704だけが 1%水準で有意でした。つまり、教育費と住居可能面積が同じならば、人口が1%上昇すると、県内総生産額が0.704%上昇すると解釈できます。
model = "within" とすると fixed effect estimationになります。
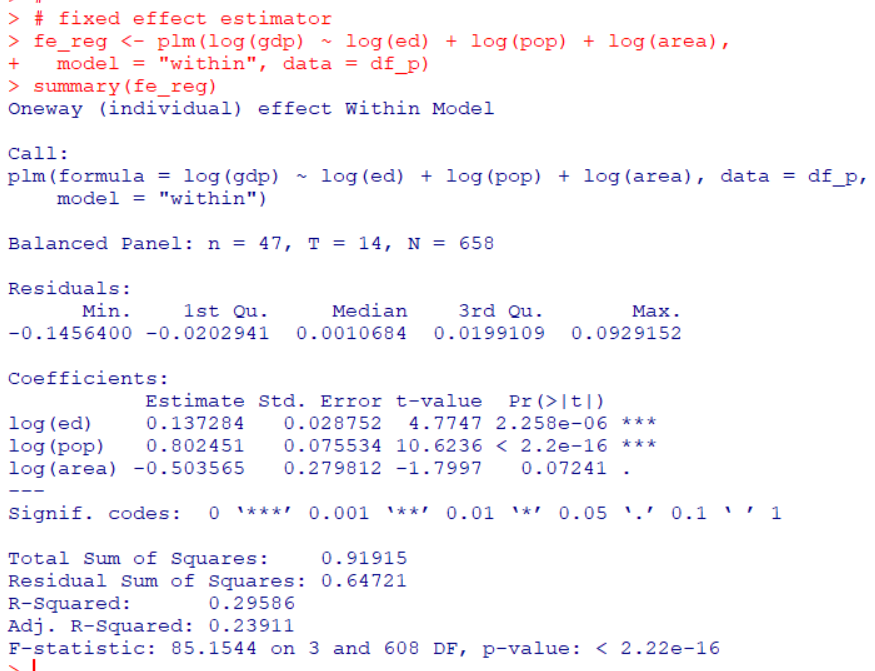
log(gdp) = 0.137 * log(ed) + 0.802 * log(pop) -0.504 * log(area) + u
と推計されました。log(ed)の係数は0.01%水準で有意でした。
人口と住居可能面積が変わらずに、教育費が1%上昇すると県内総生産額が0.137%上昇すると解釈できます。
model = "random" でrandom effects model です。

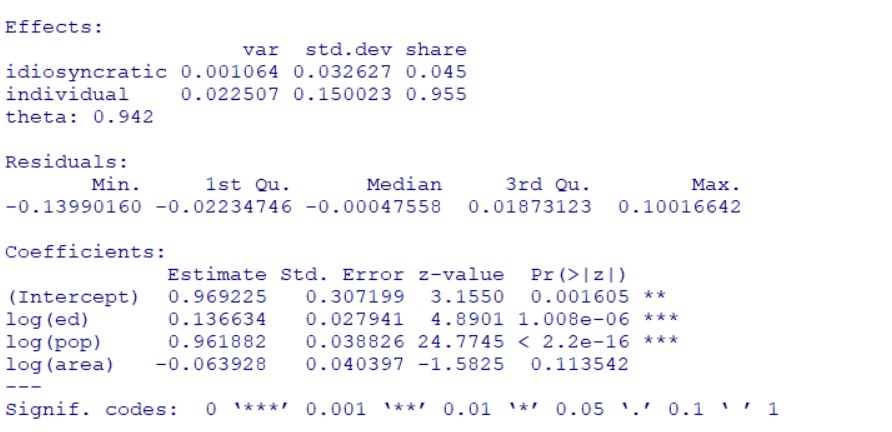
log(gdp) = 0.969 + 0.137 * log(ed) + 0.962 * log(pop) - 0.064 * log(area) + u
と推計できました。log(ed)とlog(pop)の係数は0.1%水準で有意です。
人口と住居可能面積が変わらずに、教育費が1%上昇すると、県内総生産額が0.137%上昇します。fixed effect estimator とrandom effect estimator は教育費は同じ係数の値ですね。
最後に4つのモデルのlog(ed)の係数の推測結果をまとめて表示します。
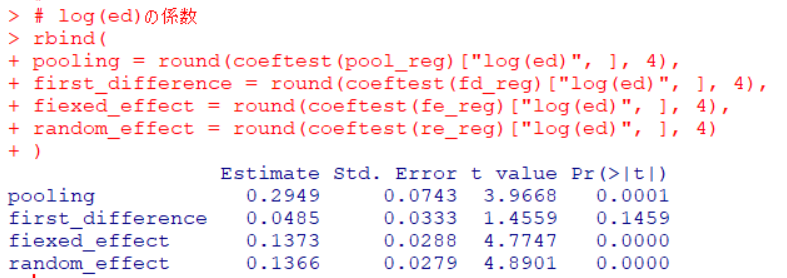
4つの推計方法ですべて係数の符号はプラスで、そのうち3つは有意な水準で推計できましたので、人口と住居可能面積が変わらなければ、教育費が上昇すると県内総生産額が上昇すると言えるのかな? あ、でも県内総生産額の中に教育費が含まれているでしょうから、当たり前と言えば当たり前ですかね。教育費を差し引いた県内総生産額で調べたほうがいいですね。
今回は以上です。
初めから読むには、
になります。