
の続きです。
今回は、データフレームを少し変形します。

このように、保護観察処分の1号、2号、3号、4号が一つの type の列におさまっているのを、

このように、1号は1号の列、2号は2号の列と別々にします。
これは、pivot_wider()を使います。

このようにします。
names_from = で新しく列名(変数名)になるデータが入っている列を指定して、
values_from = でそこに入るデータが入っている列を指定します。
typeの列に1号、2号、3号、4号が入っているので、これをnames_from = で指定して、numの列に実際の人数が入っていますからvalues_from = でnumを指定します。
さらにrename()で列名をアルファベットに変換しました。
summary()関数で新しいデータフレームのサマリーを表示してみます。

ここで、もう一度、保護観察処分の各号を確認しておきます。
保護観察(ほごかんさつ)とは? 意味や使い方 - コトバンク (kotobank.jp)
によりますと、
1号は、保護処分として家庭裁判所の決定により保護観察に付された者。
2号は、少年院を仮退院した者。
3号は、少年院を仮釈放された者。
4号は、刑の執行を猶予され保護観察に付された者。
です。
2号と4号が少なく、1号と3号が多いですね。
それでは、これらの散布図マトリックスを描いてみます。
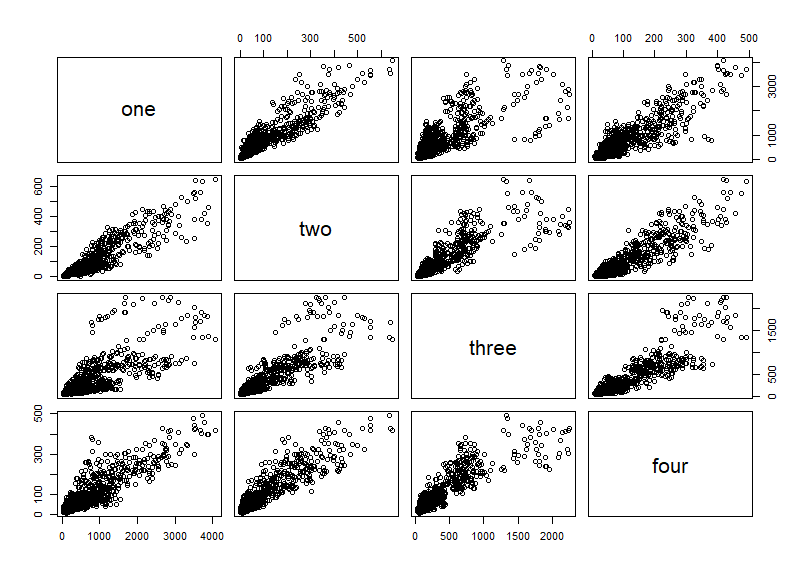
どの組み合わせも正の相関関係がありますね。
相関係数マトリックスをみてみます。

一番相関係数の低い組み合わせでもoneとthreeの0.77です。
散布図マトリックスを見ると、値の小さいエリアにデータが集中しているようなので、対数変換したデータで同じように散布図マトリックスを描いてみます。


散布図の各プロットがまんべんなく散らばっています。
相関係数マトリックスも作成してみます。

相関係数の一番低い組み合わせは、1_oneとl_threeで0.79です。
一番高い組み合わせは、l_oneとl_twoで0.91です。
今度は、1号、2号、3号、4号のそれぞれの比率を計算して、これを散布図マトリックスにしてみます。


お、さきほどまでとは違う傾向になりました。r_oneとr_threeがはっきりと逆相関ですね。
相関係数マトリックスを算出します。

マイナス相関の組み合わせばかりで、プラスの相関は、r_threeとr_fourだけでした。
今回は以上です。
次回は、
です。
初めから読むには、
です。