
Generated by Bing Image Creator: Photographic of summer festival, beautiful flowers and landscape
の続きです。
今回は非説明変数をmoku_not(木造の長屋建住宅数 / 非木造の長屋建住宅数)にしてみます。
回帰分析をする前に、散布図を描いてみます。

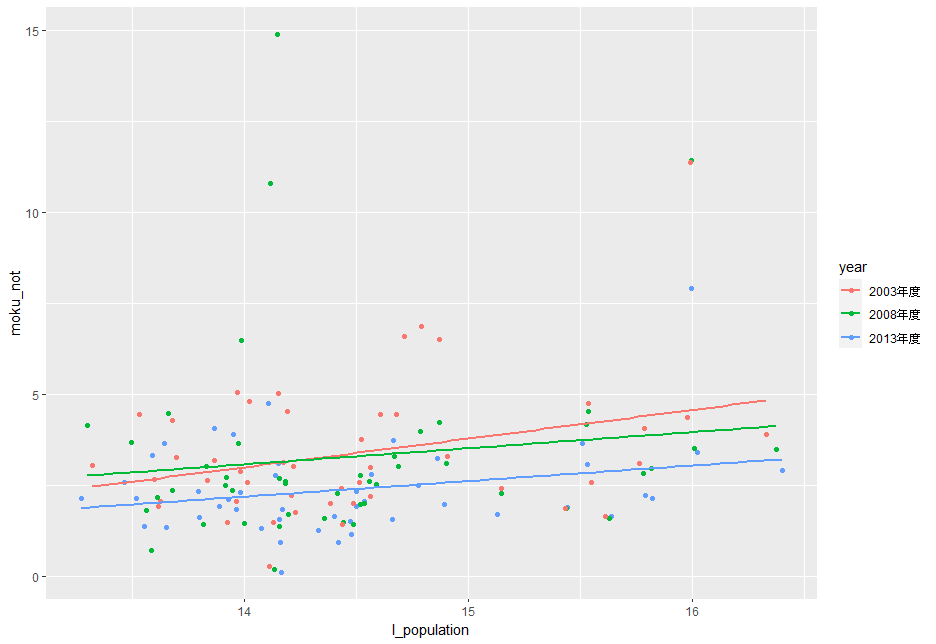

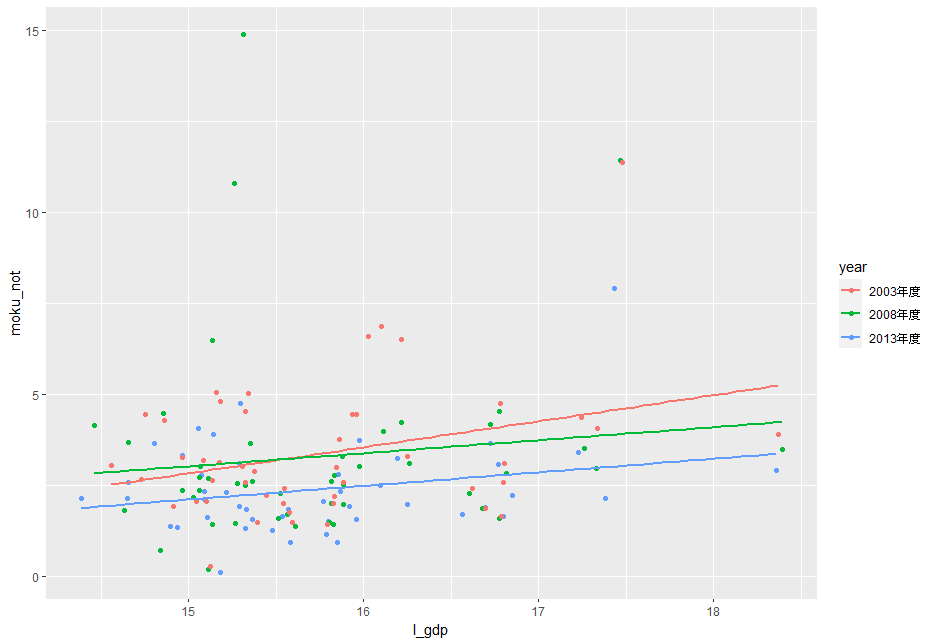
散布図を見ると、年度によって違いがありそうですね。
早速、lm()関数で回帰分析してみましょう。

year2013年度の係数のp値は有意な水準ですが、l_populationとl_gdpの係数のp値は有意な水準ではありません。l_gdpを削除したモデルを作成して、anova()関数で比較します。

anova()関数でlm_mod3とlm_mod4は有意な違いはありませんとわかりました。よって、よりシンプルなlm_mod4を採用します。
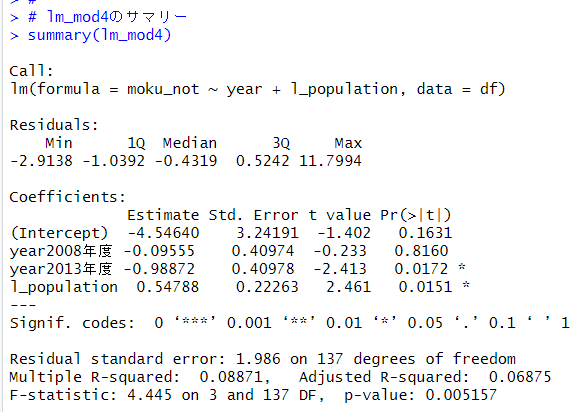
l_populationの係数のp値が0.05より小さくなりました。l_populationはmoku_notに影響のある変数です。プラスの係数なので、人口が多い都道府県ほど、moku_notの値は大きくなります。年度は、2003年が基準で、2013年は統計的に有意な水準で2003年と違っています。-0.98872とあるので、約1だけ2003年と2013年では違うということです。
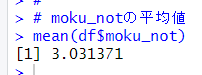
moku_not全体の平均値は3ぐらいですから、1ぐらいの変化はかなり大きな変化です。2003年から2013年の10年間で、木造の長屋建住宅数が非木造の長屋建住宅数に比べて大きく減ったことが推測されます。
グラフで確認してみます。

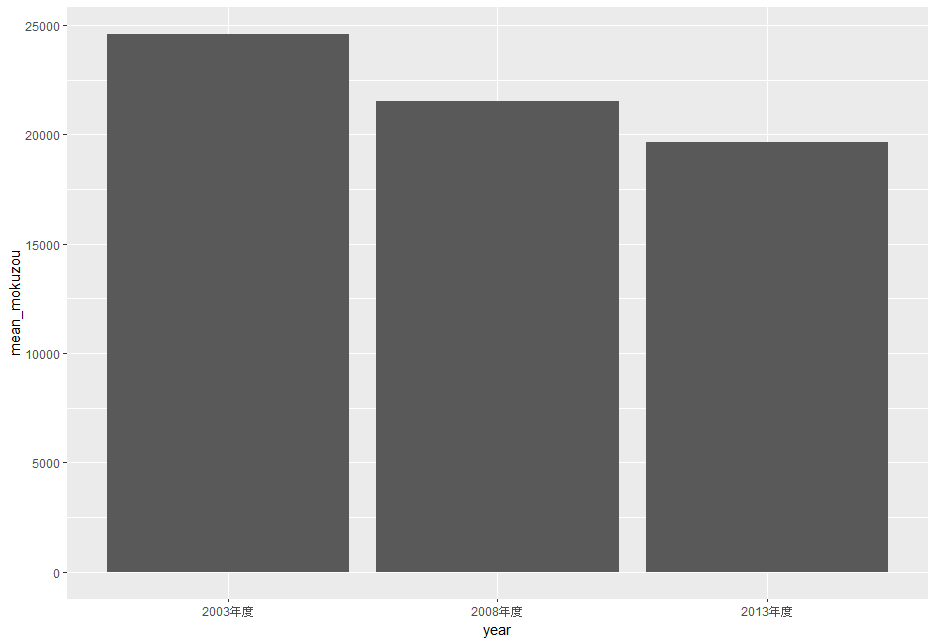
たしかに減少しています。
残差の分散が均一分散かどうかを調べてみます。

モデル全体のp値は0.2068、各説明変数の係数のp値も0.05より大きいので、残差は不均一分散とはいえませんね。
今回の回帰分析では、木造の長屋建住宅数 / 非木造の長屋建住宅数 の比率は、2003年と2013年では、2013年が減少している、人口が多い都道府県ほど、比率は高い、ということがわかりました。
今回は以上です。
次回は、
です。
初めから読むには、
です。